IB Mathematics SL 4.7 Discrete and continuous random variables AA SL Paper 2- Exam Style Questions- New Syllabus
Question
- 10 points if both dice display the same number.
- 5 points if the numerical difference between the two dice is exactly 1 (e.g., 2 and 3).
- 0 points for any other combination.
Most-appropriate topic codes (Mathematics: analysis and approaches guide):
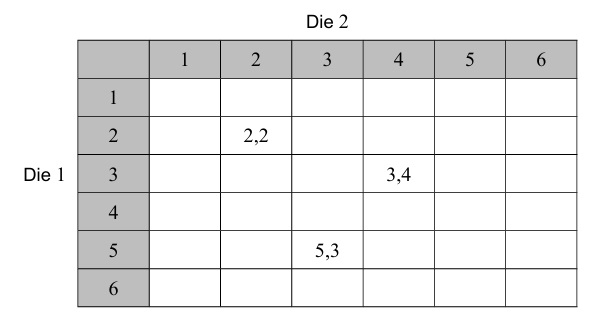
• SL 4.6: Use of tables of outcomes to calculate probabilities — Part b, e
• SL 4.7: Discrete random variables and their probability distributions; expected value \( E(X) \) — Part c
• SL 4.8: Situations where the binomial distribution is an appropriate model — Part d, e
▶️ Answer/Explanation
(a)
Total possible outcomes when throwing two dice: \( 6 \times 6 = 36 \).
Outcomes where the difference is 1:
(1,2), (2,1), (2,3), (3,2), (3,4), (4,3), (4,5), (5,4), (5,6), (6,5).
There are 10 such outcomes.
\( P(X=5) = \frac{10}{36} = \frac{5}{18} \).
(b)
Identify outcomes for other point values:
– 10 points (same score): (1,1), (2,2), (3,3), (4,4), (5,5), (6,6) → 6 outcomes.
– 5 points (difference of 1): 10 outcomes (found in part a).
Remaining outcomes for 0 points: \( 36 – (6 + 10) = 20 \).
\( P(X=0) = \frac{20}{36} = \frac{5}{9} \).
(c)
The probability distribution for \( X \) is:
\( P(X=0) = \frac{20}{36} \), \( P(X=5) = \frac{10}{36} \), \( P(X=10) = \frac{6}{36} \).
\( E(X) = \sum x \cdot P(X=x) \)
\( E(X) = \left( 0 \cdot \frac{20}{36} \right) + \left( 5 \cdot \frac{10}{36} \right) + \left( 10 \cdot \frac{6}{36} \right) \)
\( E(X) = 0 + \frac{50}{36} + \frac{60}{36} = \frac{110}{36} = \frac{55}{18} \approx 3.06 \).
(d)
Expected total score = Number of rounds \(\times E(X)\).
Total points \( = 90 \times \frac{55}{18} = 5 \times 55 = 275 \).
(e)
To win the prize (total > 40 points) in 5 rounds, Lynn must score either:
1. 50 points: (10, 10, 10, 10, 10) → all five rounds are 10-point rounds.
2. 45 points: One 5-point round and four 10-point rounds.
Let \( p_{10} = \frac{6}{36} = \frac{1}{6} \) and \( p_{5} = \frac{10}{36} = \frac{5}{18} \).
– Prob(50 pts) \( = (p_{10})^5 = \left( \frac{1}{6} \right)^5 = \frac{1}{7776} \).
– Prob(45 pts) \( = \binom{5}{1} \times (p_5)^1 \times (p_{10})^4 = 5 \times \frac{5}{18} \times \left( \frac{1}{6} \right)^4 = \frac{25}{23328} \).
Total probability \( = \frac{3}{23328} + \frac{25}{23328} = \frac{28}{23328} = \frac{7}{5832} \approx 0.00120 \).