Question
A transformation, T, of a plane is represented by \(r’ = Pr + q\), where P is a \(2 \times 2\) matrix, q is a \(2 \times 1\) vector, r is the position vector of a point i the plane and r’ the position vector of its image under T.
The triangle OAB has coordinates (0, 0), \((\frac{1}{4}, 1 + \frac{\sqrt{3}}{4})\) and \((\frac{\sqrt{3}}{4}, \frac{3}{4}\)) respectively.
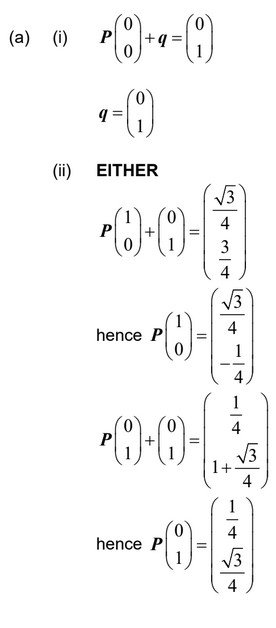
(a) (i) By considering the image of (0 , 0), find q.
(ii) By considering the image of (1 , 0) and (0 , 1), show that
\(P = \begin{pmatrix}
\frac{\sqrt{3}}{4} & \frac{1}{4}\\
-\frac{1}{4} & \frac{\sqrt{3}}{4}
\end{pmatrix}\)
P can be written as P = RS, where S and R are matrices.
S represents an enlargement with scale factor 0.5, centre (0 , 0).
R represents a rotation about (0 , 0).
(b) Write down the matrix S.
(c) (i) Use P = RS to find the matrix R.
(ii) Hence find the angle and direction of the rotation represented by R.
The transformation T can also be described by an enlargement scale factor \(\frac{1}{2}\) centre (a,b), followed by a rotation about the same centre (a, b)
(d) (i) Write down an equation satisfied by \(\binom{a}{b}\)
(ii) Find the value of a and the value of b.
▶️Answer/Explanation
Ans:
Question
Consider the matrix
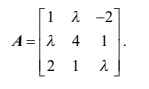
Show that 3 is the only real value of λ for which A is singular. [4]
Consider the system of equations
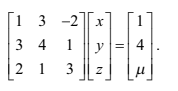
Determine the value of μ for which the equations are consistent.
Solve the equations in that case. [6]
Consider the system of equations
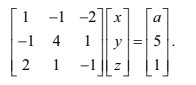
where a is an integer.
Find the inverse of the matrix of coefficients, giving the answer in exact form.
Given that y = x2 , determine the value of a and hence the value of x and of y . [9]
▶️Answer/Explanation
Ans:
(a)
attempts to find det A
\(det A = 4 \lambda -1+\lambda (2-\lambda ^{2})- 2(\lambda -8)=(-\lambda ^{3}+4\lambda +15)\)
recognises that A is singular when det A = O
solves to obtain \(\lambda =3,(-1.5\pm 1.66i)\) and
demonstrates that the only real root is 3 for which A is singular
(b)
(i)
attempts row reduction
for example, \(R_2-3R_1\) and \(R_3-2R_1\)
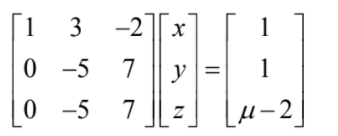
\(\mu -2=1\)
⇒ μ =3
(ii)
attempts to solve by putting z =α ,for example,
y= \(\frac{7a-1}{5},x = \frac{8-11a}{5}\)
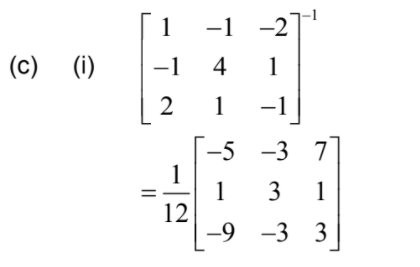
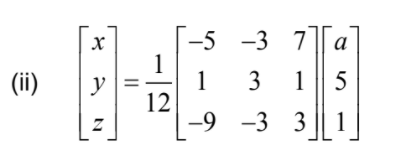
attempts to find the RHS matrix product
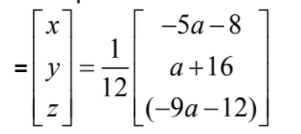
y= \(x^{2}\Rightarrow \frac{a+16}{12}=\frac{(-5a- 8)^{2}}{144}\)
\(\Rightarrow 25a^{2}\)+68a-128= 0
a = -4
x= y = 1
Question
The matrix A is given by
A =
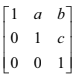where a , b , c ∈ R. Verify that the inverse matrix of A is given by
A-1 =
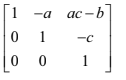[2]The set of matrices
,where a , b , c ∈ R. is denoted by S .Show that {S , *} is a group, where * denotes matrix multiplication. It may be assumed that matrix multiplication is associative.
Determine whether {S , *} is Abelian.
Identify any self-inverse elements of {S , *} . [11]
The set of matrices
where a , b , c ∈ R , is denoted by T .
Giving a reason, state whether {T , *} is a subgroup of {S , *} . [1]
▶️Answer/Explanation
Ans:
(a)
EITHER
forms AA-1
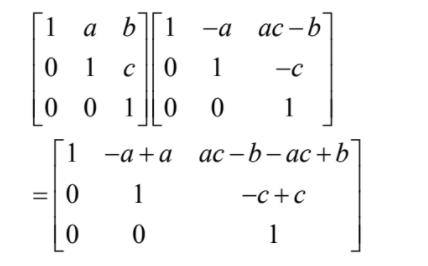
OR
FROMS A-1 A
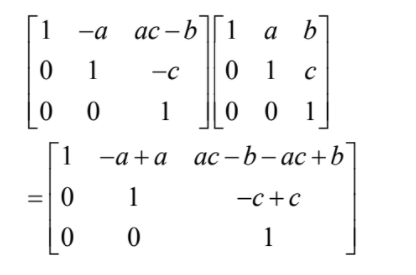
THEN
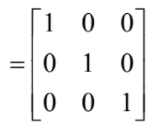which proves the result
(b)
(i)
closure:
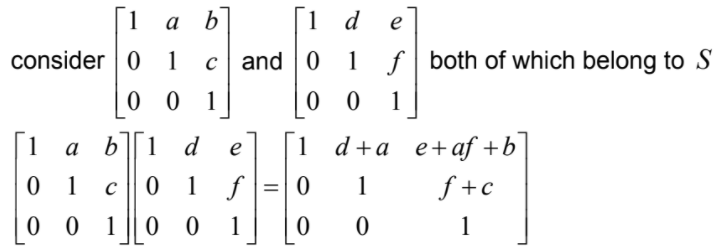
which belongs to S , therefore closed
identity:
putting a,b, c = O , the identity matrix is seen to belong to S
inverse:
it has been shown in (a) that a matrix belonging to S has an inverse in S
associativity:
this follows since matrix multiplication is associative the four group axioms are satisfied therefore {S *} is a group
(ii)
consider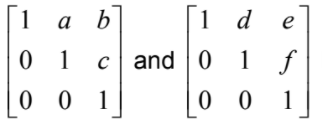 
both of which belong to S
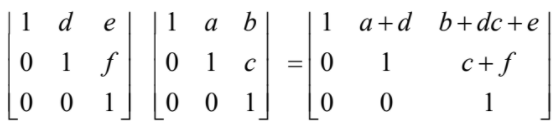
this is different from the reverse product found above so {S *} is not Abelian
(iii)
EITHER
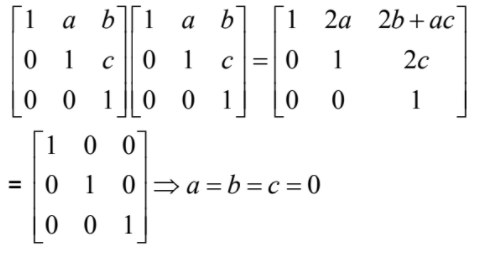
OR
compares A and A-1
determines from this comparison that a= b= c = o
THEN the only self-inverse element is therefore the identity matrix
(c) yes because the identity, inverse and the product would belong to T
Question
The set of all permutations of the list of the integers \(1,{\text{ }}2,{\text{ }}3{\text{ }} \ldots {\text{ }}n\) is a group, \({S_n}\), under the operation of composition of permutations.
a.Each element of \({S_4}\) can be represented by a \(4 \times 4\) matrix. For example, the cycle \({\text{(1 2 3 4)}}\) is represented by the matrix
\(\left( {\begin{array}{*{20}{c}} 0&1&0&0 \\ 0&0&1&0 \\ 0&0&0&1 \\ 1&0&0&0 \end{array}} \right)\) acting on the column vector \(\left( {\begin{array}{*{20}{c}} 1 \\ 2 \\ 3 \\ 4 \end{array}} \right)\).
(i) Show that the order of \({S_n}\) is \(n!\);
(ii) List the 6 elements of \({S_3}\) in cycle form;
(iii) Show that \({S_3}\) is not Abelian;
(iv) Deduce that \({S_n}\) is not Abelian for \(n \geqslant 3\).[9]
b.(i) Write down the matrices M\(_1\), M\(_2\) representing the permutations \((1{\text{ }}2),{\text{ }}(2{\text{ }}3)\), respectively;
(ii) Find M\(_1\)M\(_2\) and state the permutation represented by this matrix;
(iii) Find \(\det (\)M\(_1)\), \(\det (\)M\(_2)\) and deduce the value of \(\det (\)M\(_1\)M\(_2)\).[7]
c.(i) Use mathematical induction to prove that
\((1{\text{ }}n)(1{\text{ }}n{\text{ }} – 1)(1{\text{ }}n – 2) \ldots (1{\text{ }}2) = (1{\text{ }}2{\text{ }}3 \ldots n){\text{ }}n \in {\mathbb{Z}^ + },{\text{ }}n > 1\).
(ii) Deduce that every permutation can be written as a product of cycles of length 2.[8]
▶️Answer/Explanation
Markscheme
(i) 1 has \(n\) possible new positions; 2 then has \(n – 1\) possible new positions…
\(n\) has only one possible new position R1
the number of possible permutations is \(n \times (n – 1) \times \ldots \times 2 \times 1\) R1
\( = n!\) AG
Note: Give no credit for simply stating that the number of permutations is \(n!\)
(ii) \((1)(2)(3);{\text{ }}(1{\text{ }}2)(3);{\text{ }}(1{\text{ }}3)(2);{\text{ }}(2{\text{ }}3)(1);{\text{ }}(1{\text{ }}2{\text{ }}3);{\text{ }}(1{\text{ }}3{\text{ }}2)\) A2
Notes: A1 for 4 or 5 correct.
If single bracket terms are missing, do not penalize.
Accept \(e\) in place of the identity.
(iii) attempt to compare \({\pi _1} \circ {\pi _2}\) with \({\pi _2} \circ {\pi _1}\) for two permutations M1
for example \((1{\text{ }}2)(1{\text{ }}3) = (1{\text{ }}3{\text{ }}2)\) A1
but \((1{\text{ }}3)(1{\text{ }}2) = (1{\text{ }}2{\text{ }}3)\) A1
hence \({S_3}\) is not Abelian AG
(iv) \({S_3}\) is a subgroup of \({S_n}\), R1
so \({S_n}\) contains non-commuting elements R1
\( \Rightarrow {S_n}\) is not Abelian for \(n \geqslant 3\) AG
[9 marks]
(i) M\(_1 = \left( {\begin{array}{*{20}{c}} 0&1&0&0 \\ 1&0&0&0 \\ 0&0&1&0 \\ 0&0&0&1 \end{array}} \right)\), M\(_2 = \left( {\begin{array}{*{20}{c}} 1&0&0&0 \\ 0&0&1&0 \\ 0&1&0&0 \\ 0&0&0&1 \end{array}} \right)\) A1A1
(ii) M\(_1\)M\(_2 = \left( {\begin{array}{*{20}{c}} 0&0&1&0 \\ 1&0&0&0 \\ 0&1&0&0 \\ 0&0&0&1 \end{array}} \right)\) A1
this represents \((1{\text{ }}3{\text{ }}2)\) A1
(iii) by, for example, interchanging a pair of rows (M1)
\(\det (\)M\(_1) = \det (\)M\(_2) = – 1\) A1
then \(\det (\)M\(_1\)M\(_2) = ( – 1) \times ( – 1) = 1\) A1
[7 marks]
(i) let \({\text{P}}(n)\) be the proposition that
\((1{\text{ }}n)(1{\text{ }}n – 1)(1{\text{ }}n – 2) \ldots (1{\text{ }}2) = (1{\text{ }}2{\text{ }}3 \ldots n){\text{ }}n \in {\mathbb{Z}^ + }\)
the statement that \({\text{P}}(2)\) is true eg \((1{\text{ }}2) = (1{\text{ }}2)\) A1
assume \({\text{P}}(k)\) is true for some \(k\) M1
consider \((1{\text{ }}k + 1)(1{\text{ }}k)(1{\text{ }}k – 1)(1{\text{ }}k – 2) \ldots (1{\text{ }}2)\)
\( = (1{\text{ }}k + 1)(1{\text{ }}2{\text{ }}3 \ldots k)\) M1
then the composite permutation has the following effect on the first \(k + 1\) integers: \(1 \to 2,{\text{ }}2 \to 3 \ldots k – 1 \to k,{\text{ }}k \to 1 \to k + 1,{\text{ }}k + 1 \to 1\) A1
this is \((1{\text{ }}2{\text{ }}3 \ldots k{\text{ }}k + 1)\) A1
hence the assertion is true by induction AG
(ii) every permutation is a product of cycles R1
generalizing the result in (i) R1
every cycle is a product of cycles of length 2 R1
hence every permutation can be written as a product of cycles of length 2 AG
[8 marks]
Question
Consider the matrix
A \( = \left[ {\begin{array}{*{20}{c}} \lambda &3&2 \\ 2&4&\lambda \\ 3&7&3 \end{array}} \right]\).
Suppose now that \(\lambda = 1\) so consider the matrix
B \( = \left[ {\begin{array}{*{20}{c}} 1&3&2 \\ 2&4&1 \\ 3&7&3 \end{array}} \right]\).
a.i.Find an expression for det(A) in terms of \(\lambda \), simplifying your answer.[3]
a.ii.Hence show that A is singular when \(\lambda = 1\) and find the other value of \(\lambda \) for which A is singular.[2]
b.i.Explain how it can be seen immediately that B is singular without calculating its determinant.[1]
b.ii.Determine the null space of B.[4]
b.iii.Explain briefly how your results verify the rank-nullity theorem.
c.Prove, using mathematical induction, that
B\(^n = {8^{n – 2}}\)B\(^2\) for \(n \in {\mathbb{Z}^ + },{\text{ }}n \geqslant 3\).[7]
▶️Answer/Explanation
Markscheme
det(A) \( = \lambda (12 – 7\lambda ) + 3(3\lambda – 6) + 2(14 – 12)\) M1A1
\( = 12\lambda – 7{\lambda ^2} + 9\lambda – 18 + 4\)
\( = – 7{\lambda ^2} + 21\lambda – 14\) A1
[??? marks]
A is singular when \(\lambda = 1\) because the determinant is zero R1
Note: Do not award the R1 if the determinant has not been obtained.
the other value is 2 A1
[??? marks]
the third row is the sum of the first two rows A1
[??? marks]
the null space satisfies
\(\left[ {\begin{array}{*{20}{c}} 1&3&2 \\ 2&4&1 \\ 3&7&3 \end{array}} \right]\left[ {\begin{array}{*{20}{c}} x \\ y \\ z \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} 0 \\ 0 \\ 0 \end{array}} \right]\) M1
\(x + 3y + 2z = 0\)
\(2x + 4y + z = 0\) (A1)
\(3x + 7y + 3z = 0\)
the solution is (by GDC or otherwise)
\(\left[ {\begin{array}{*{20}{c}} x \\ y \\ z \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} 5 \\ { – 3} \\ 2 \end{array}} \right]\alpha \) where \(\alpha \in \mathbb{R}\) M1A1
[??? marks]
the rank-nullity theorem for square matrices states that
rank of matrix + dimension of null space = number of columns A1
here, rank = 2, dimension of null space = 1 and number of columns = 3 A1
[??? marks]
first show that the result is true for \(n = 3\)
B\(^2 = \left[ {\begin{array}{*{20}{c}} {13}&{29}&{11} \\ {13}&{29}&{11} \\ {26}&{58}&{22} \end{array}} \right]\) A1
B\(^3 = \left[ {\begin{array}{*{20}{c}} {104}&{232}&{88} \\ {104}&{232}&{88} \\ {208}&{464}&{176} \end{array}} \right]\) A1
therefore B\(^3 = 8\)B\(^2\) so true for \(n = 3\) R1
assume the result is true for \(n = k\), that is B\(^k = {8^{k – 2}}\)B\(^2\) M1
consider B\(^{k + 1} = {8^{k – 2}}\)B\(^2\) M1
\( = {8^{k – 2}}8\)B\(^2\)
\( = {8^{k – 1}}\)B\(^2\) A1
therefore, true for \(n = k \Rightarrow \) true for \(n = k + 1\) and since the result is true for \(n = 3\), it is true for \(n \geqslant 3\) R1
[7 marks]