Question
Consider the matrix M = \(\left[ {\begin{array}{*{20}{c}}
2 \\
{ – 1}
\end{array}\,\,\,\begin{array}{*{20}{c}}
{ – 4} \\
{ – 1}
\end{array}} \right]\).
a.Show that the linear transformation represented by M transforms any point on the line \(y = x\) to a point on the same line.[2]
b.Explain what happens to points on the line \(4y + x = 0\) when they are transformed by M.[3]
c.State the two eigenvalues of M.[2]
d.State two eigenvectors of M which correspond to the two eigenvalues.[2]
▶️Answer/Explanation
Markscheme
\(\left( {\begin{array}{*{20}{c}}
2 \\
{ – 1}
\end{array}\,\,\,\begin{array}{*{20}{c}}
{ – 4} \\
{ – 1}
\end{array}} \right)\left( {\begin{array}{*{20}{c}}
k \\
k
\end{array}} \right) = \left( {\begin{array}{*{20}{c}}
{ – 2k} \\
{ – 2k}
\end{array}} \right)\left( { = – 2\left( {\begin{array}{*{20}{c}}
k \\
k
\end{array}} \right)} \right)\) M1A1
hence still on the line \(y = x\) AG
[2 marks]
consider \(\left( {\begin{array}{*{20}{c}}
2 \\
{ – 1}
\end{array}\,\,\,\begin{array}{*{20}{c}}
{ – 4} \\
{ – 1}
\end{array}} \right)\left( {\begin{array}{*{20}{c}}
{4k} \\
{ – k}
\end{array}} \right)\) M1
\( = \left( {\begin{array}{*{20}{c}}
{12k} \\
{ – 3k}
\end{array}} \right)\left( { = 3\left( {\begin{array}{*{20}{c}}
{4k} \\
{ – k}
\end{array}} \right)} \right)\) A1
hence the line is invariant A1
[3 marks]
hence the eigenvalues are −2 and 3 A1A1
[2 marks]
\(\left( {\begin{array}{*{20}{c}}
1 \\
1
\end{array}} \right)\) and \(\left( {\begin{array}{*{20}{c}}
4 \\
{ – 1}
\end{array}} \right)\) or equivalent A1A1
[2 marks]
Question
Consider the matrix M = \(\left[ {\begin{array}{*{20}{c}}
2 \\
{ – 1}
\end{array}\,\,\,\begin{array}{*{20}{c}}
{ – 4} \\
{ – 1}
\end{array}} \right]\).
a.Show that the linear transformation represented by M transforms any point on the line \(y = x\) to a point on the same line.[2]
b.Explain what happens to points on the line \(4y + x = 0\) when they are transformed by M.[3]
c.State the two eigenvalues of M.[2]
d.State two eigenvectors of M which correspond to the two eigenvalues.[2]
▶️Answer/Explanation
Markscheme
\(\left( {\begin{array}{*{20}{c}}
2 \\
{ – 1}
\end{array}\,\,\,\begin{array}{*{20}{c}}
{ – 4} \\
{ – 1}
\end{array}} \right)\left( {\begin{array}{*{20}{c}}
k \\
k
\end{array}} \right) = \left( {\begin{array}{*{20}{c}}
{ – 2k} \\
{ – 2k}
\end{array}} \right)\left( { = – 2\left( {\begin{array}{*{20}{c}}
k \\
k
\end{array}} \right)} \right)\) M1A1
hence still on the line \(y = x\) AG
[2 marks]
consider \(\left( {\begin{array}{*{20}{c}}
2 \\
{ – 1}
\end{array}\,\,\,\begin{array}{*{20}{c}}
{ – 4} \\
{ – 1}
\end{array}} \right)\left( {\begin{array}{*{20}{c}}
{4k} \\
{ – k}
\end{array}} \right)\) M1
\( = \left( {\begin{array}{*{20}{c}}
{12k} \\
{ – 3k}
\end{array}} \right)\left( { = 3\left( {\begin{array}{*{20}{c}}
{4k} \\
{ – k}
\end{array}} \right)} \right)\) A1
hence the line is invariant A1
[3 marks]
hence the eigenvalues are −2 and 3 A1A1
[2 marks]
\(\left( {\begin{array}{*{20}{c}}
1 \\
1
\end{array}} \right)\) and \(\left( {\begin{array}{*{20}{c}}
4 \\
{ – 1}
\end{array}} \right)\) or equivalent A1A1
[2 marks]
Question
The matrix M is defined by M = \(\left( {\begin{array}{*{20}{c}}a&b\\c&d\end{array}} \right)\).
The eigenvalues of M are denoted by \({\lambda _1},{\text{ }}{\lambda _2}\).
(a) Show that \({\lambda _1} + {\lambda _2} = a + d\) and \({\lambda _1}{\lambda _2} = \det \)(M).
(b) Given that \(a + b = c + d = 1\), show that 1 is an eigenvalue of M.
(c) Find eigenvectors for the matrix \(\left( {\begin{array}{*{20}{c}}2&{ – 1}\\3&{ – 2}\end{array}} \right)\).
▶️Answer/Explanation
Markscheme
(a) the eigenvalues satisfy \(\left| {\begin{array}{*{20}{c}} {a – \lambda }&b \\ c&{d – \lambda } \end{array}} \right| = 0\) (M1)
\({\lambda ^2} – (a + d)\lambda + ad – bc = 0\) A1
using the sum and product properties of the roots of a quadratic equation R1
\({\lambda _1} + {\lambda _2} = a + d,{\text{ }}{\lambda _1}{\lambda _2} = ad – bc = \det \,\)(M) AG
[3 marks]
(b) let \(f(\lambda ) = {\lambda ^2} – (a + d)\lambda + ad – bc\)
putting \(b = 1 – a\) and \(d = 1 – c\), consider M1
\(f(1) = 1 – a – 1 + c + a – ac – c + ac = 0\) A1
therefore \(\lambda = 1\) is an eigenvalue AG
[2 marks]
Note: Allow substitution for \(b\), \(c\) into the quadratic equation for \(\lambda \) followed by solution of this equation.
(c) using any valid method (M1)
the eigenvalues are 1 and –1 A1
an eigenvector corresponding to \(\lambda = 1\) satisfies
\(\left( {\begin{array}{*{20}{c}}2&{ – 1}\\3&{ – 2}\end{array}} \right)\left( \begin{array}{l}x\\y\end{array} \right) = \left( \begin{array}{l}x\\y\end{array} \right)\) or \(\left( {\begin{array}{*{20}{c}}1&{ – 1}\\3&{ – 3}\end{array}} \right)\left( \begin{array}{l}x\\y\end{array} \right) = \left( \begin{array}{l}0\\0\end{array} \right)\) M1A1
\(\left( \begin{array}{l}x\\y\end{array} \right) = \left( \begin{array}{l}1\\1\end{array} \right)\) or any multiple A1
an eigenvector corresponding to \(\lambda = – 1\) satisfies
\(\left( {\begin{array}{*{20}{c}}2&{ – 1}\\3&{ – 2}\end{array}} \right)\left( \begin{array}{l}x\\y\end{array} \right) = – \left( \begin{array}{l}x\\y\end{array} \right)\) or \(\left( {\begin{array}{*{20}{c}}3&{ – 1}\\3&{ – 1}\end{array}} \right)\left( \begin{array}{l}x\\y\end{array} \right) = \left( \begin{array}{l}0\\0\end{array} \right)\) M1
\(\left( \begin{array}{l}x\\y\end{array} \right) = \left( \begin{array}{l}1\\3\end{array} \right)\) or any multiple A1
Note: Award M1A1A1 for calculating the first eigenvector and M1A1 for the second irrespective of the order in which they are calculated.
[7 marks]
Question
Given that the elements of a \(2 \times 2\) symmetric matrix are real, show that
a. (i) the eigenvalues are real;
(ii) the eigenvectors are orthogonal if the eigenvalues are distinct.[11]
{11}&{\sqrt 3 }\\
{\sqrt 3 }&9
\end{array}} \right) .\]Find the eigenvalues and eigenvectors of \(\boldsymbol{A}\).[7]
x\\
y
\end{array} \right)\) and \(\boldsymbol{A}\) is as defined in part (b).
(i) Show that \(E\) can be rotated about the origin onto the ellipse \(E’\) having equation \(2{x^2} + 3{y^2} = 6\) .
(ii) Find the acute angle through which \(E\) has to be rotated to coincide with \(E’\) .[7]
▶️Answer/Explanation
Markscheme
(i) let \(\boldsymbol{M} = \left( {\begin{array}{*{20}{c}}
a&b\\
b&c
\end{array}} \right)\) (M1)
the eigenvalues satisfy
\(\det (\boldsymbol{M} – \lambda \boldsymbol{I}) = 0\) (M1)
\((a – \lambda )(c – \lambda ) – {b^2} = 0\) (A1)
\({\lambda ^2} – \lambda (a + c) + ac – {b^2} = 0\) A1
discriminant \( = {(a + c)^2} – 4(ac – {b^2})\) M1
\( = {(a – c)^2} + 4{b^2} \ge 0\) A1
this shows that the eigenvalues are real AG
(ii) let the distinct eigenvalues be \({\lambda _1},{\lambda _2}\) , with eigenvectors \({{\boldsymbol{X}}_1}\), \({{\boldsymbol{X}}_2}\)
then
\({\lambda _1}{{\boldsymbol{X}}_1} = {\boldsymbol{M}}{{\boldsymbol{X}}_1}\) and \({\lambda _2}{{\boldsymbol{X}}_2} = {\boldsymbol{M}}{{\boldsymbol{X}}_1}\) M1
transpose the first equation and postmultiply by \({{\boldsymbol{X}}_2}\) to give
\({\lambda _1}{\boldsymbol{X}}_1^T{{\boldsymbol{X}}_2} = {\boldsymbol{X}}_1^T{\boldsymbol{M}}{{\boldsymbol{X}}_2}\) A1
premultiply the second equation by \({\boldsymbol{X}}_1^T\)
\({\lambda _2}{\boldsymbol{X}}_1^T{{\boldsymbol{X}}_2} = {\boldsymbol{X}}_1^T{\boldsymbol{M}}{{\boldsymbol{X}}_2}\) A1
it follows that
\((\lambda 1 – {\lambda _2}){\boldsymbol{X}}_1^T{{\boldsymbol{X}}_2} = 0\) A1
since \(\lambda 1 \ne {\lambda _2}\) , it follows that \({\boldsymbol{X}}_1^T{{\boldsymbol{X}}_2} = 0\) so that the eigenvectors are orthogonal R1
[11 marks]
the eigenvalues satisfy \(\left| \begin{array}{l}
11 – \lambda \\
\sqrt 3
\end{array} \right.\left. \begin{array}{l}
\sqrt 3 \\
9 – \lambda
\end{array} \right| = 0\) M1A1
\({\lambda ^2} – 20\lambda + 96 = 0\) A1
\(\lambda = 8,12\) A1
first eigenvector satisfies
\(\left( {\begin{array}{*{20}{c}}
3&{\sqrt 3 }\\
{\sqrt 3 }&1
\end{array}} \right)\left( \begin{array}{l}
x\\
y
\end{array} \right) = \left( \begin{array}{l}
0\\
0
\end{array} \right)\) M1
\(\left( \begin{array}{l}
x\\
y
\end{array} \right) = \) (any multiple of) \(\left( {\begin{array}{*{20}{c}}
1\\
{ – \sqrt 3 }
\end{array}} \right)\) A1
second eigenvector satisfies
\(\left( {\begin{array}{*{20}{c}}
{ – 1}&{\sqrt 3 }\\
{\sqrt 3 }&{ – 3}
\end{array}} \right)\left( \begin{array}{l}
x\\
y
\end{array} \right) = \left( \begin{array}{l}
0\\
0
\end{array} \right)\)
\(\left( \begin{array}{l}
x\\
y
\end{array} \right) = \) (any multiple of ) \(\left( {\begin{array}{*{20}{c}}
{\sqrt 3 }\\
1
\end{array}} \right)\) A1
[7 marks]
(i) consider the rotation in which \((x,y)\) is transformed onto \((x’,y’)\) defined by
\(\left( \begin{array}{l}
{x’}\\
{y’}
\end{array} \right) = \left( {\begin{array}{*{20}{c}}
{\frac{1}{2}}&{ – \frac{{\sqrt 3 }}{2}}\\
{\frac{{\sqrt 3 }}{2}}&{\frac{1}{2}}
\end{array}} \right)\left( \begin{array}{l}
x\\
y
\end{array} \right)\) so that \(\left( \begin{array}{l}
x\\
y
\end{array} \right) = \left( {\begin{array}{*{20}{c}}
{\frac{1}{2}}&{\frac{{\sqrt 3 }}{2}}\\
{ – \frac{{\sqrt 3 }}{2}}&{\frac{1}{2}}
\end{array}} \right)\left( \begin{array}{l}
{x’}\\
{y’}
\end{array} \right)\) M1A1
the ellipse \(E\) becomes
\(\left( {\begin{array}{*{20}{c}}
{x’}&{y’}
\end{array}} \right)\left( {\begin{array}{*{20}{c}}
{\frac{1}{2}}&{ – \frac{{\sqrt 3 }}{2}}\\
{\frac{{\sqrt 3 }}{2}}&{\frac{1}{2}}
\end{array}} \right)\left( {\begin{array}{*{20}{c}}
{11}&{\sqrt 3 }\\
{\sqrt 3 }&9
\end{array}} \right)\left( {\begin{array}{*{20}{c}}
{\frac{1}{2}}&{\frac{{\sqrt 3 }}{2}}\\
{ – \frac{{\sqrt 3 }}{2}}&{\frac{1}{2}}
\end{array}} \right)\left( \begin{array}{l}
{x’}\\
{y’}
\end{array} \right) = 24\) M1A1
\(\left( {\begin{array}{*{20}{c}}
{x’}&{y’}
\end{array}} \right)\left( {\begin{array}{*{20}{c}}
8&0\\
0&{12}
\end{array}} \right)\left( \begin{array}{l}
{x’}\\
{y’}
\end{array} \right) = 24\) A1
\(2{(x’)^2} + 3{(y’)^2} = 6\) AG
(ii) the angle of rotation is given by \(\cos \theta = \frac{1}{2},\sin \theta = \frac{{\sqrt 3 }}{2}\) M1
since a rotational matrix has the form \(\left( {\begin{array}{*{20}{c}}
{\cos \theta }&{ – \sin \theta }\\
{\sin \theta }&{\cos \theta }
\end{array}} \right)\)
so \(\theta = {60^ \circ }\) (anticlockwise) A1
[7 marks]
[MAI 1.15] TRANSFORMATION MATRICES-loyola
Question
[Maximum mark: 5]
Let M 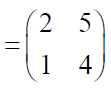 be a transformation matrix.
be a transformation matrix.
(a) The matrix M maps the point (x, y) to the point (x’, y’) . Write down two liner equations for x’ and y’ in terms of x and y . [2]
(b) Find images of the following points
(i) O(0,0) (ii) A(1,1) (iii) B(3,5). [3]
▶️Answer/Explanation
Answer:
1. (a) x’ = 2x + 5y
y’ = x + 4y
(b) The image of O(0,0) is O(0,0) itself.
The image of A(1,1) is A΄(7,5).
The image of B(3,5) is B΄(31,23).
