Question
Two lines L1 and L2 are given by the following equations, where p∈R.
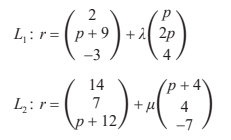
It is known that L1 and L2 are perpendicular.
a.Find the possible value(s) for p . [3]
b. In the case that p < 0 , determine whether the lines intersect. [4]
▶️Answer/Explanation
(a) setting a dot product of the direction vectors equal to zero 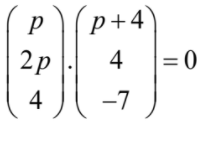
\(p(p+4)+8p – 28 = 0\)
\(p2+ 12 p +28 = 0\)
\((p + 14) (p -2 ) = 0\)
\(p =-14\) ,\( p = 2 \)
(b) p =−14 ⇒ 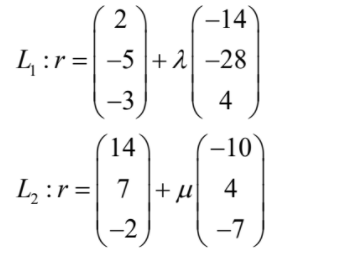
a common point would satisfy the equations
2 – 14λ = 14 -10μ …………(i)
−5−28λ = 7+ 4μ …………….(ii)
-3+ 4λ = -2-7μ ………….(iii)
METHOD 1
solving the first two equations simultaneously
\(\lambda = – \frac{1}{2}\)
\(\mu =\frac{1}{2}\)
substitute into the third equation: \(-3+ 4(-\frac{1}{2})\) ≠ \(-2+\frac{1}{2}(-7)\) so lines do not intersect.
METHOD 2 attempting to solve the equations using a GDC
GDC indicates no solution so lines do not intersect
Question
In an experiment it is found that a culture of bacteria triples in number every four hours. There are \(200\) bacteria at the start of the experiment.

a.Find the value of \(a\).[1]
b.Calculate how many bacteria there will be after one day.[2]
c.Find how long it will take for there to be two million bacteria.[3]
▶️Answer/Explanation
Markscheme
\(a = 1800\) (A1) (C1)[1 mark]
\(200 \times {3^6}{\text{ (or }}16200 \times 9{\text{) }} = 145800\) (M1)(A1) (C2)[2 marks]
\(200 \times {3^n} = 2 \times {10^6}\) (where \(n\) is each \(4\) hour interval) (M1)
Note: Award (M1) for attempting to set up the equation or writing a list of numbers.
\({3^n} = {10^4}\)
\(n = 8.38{\text{ }}(8.383613097)\) correct answer only (A1)
\({\text{Time}} = 33.5{\text{ hours}}\) (accept \(34\), \(35\) or \(36\) if previous A mark awarded) (A1)(ft) (C3)
Note: (A1)(ft) for correctly multiplying their answer by \(4\). If \(34\), \(35\) or \(36\) seen, or \(32 – 36\) seen, award (M1)(A0)(A0).[3 marks]
Question
Given the function \(f (x) = 2 \times 3^x\) for −2 \( \leqslant \) x \( \leqslant \) 5,
a.find the range of \(f\).[4]
b.find the value of \(x\) given that \(f (x) =162\).[2]
▶️Answer/Explanation
Markscheme
\(f (-2) = 2 \times 3^{-2}\) (M1)
\(= \frac{{2}}{{9}}(0.222)\) (A1)
\(f (5) = 2 \times 3^5\)
\(= 486\) (A1)
\({\text{Range }}\frac{2}{9} \leqslant f(x) \leqslant 486\) OR \(\left[ {\frac{2}{9},{\text{ }}486} \right]\) (A1) (C4)
Note: Award (M1) for correct substitution of –2 or 5 into \(f (x)\), (A1)(A1) for each correct end point.[4 marks]
\(2 \times 3^x = 162\) (M1)
\(x = 4\) (A1) (C2)[2 marks]
Question
The number of bacteria in a colony is modelled by the function
\(N(t) = 800 \times 3^{0.5t}, {\text{ }} t \geqslant 0\),
where \(N\) is the number of bacteria and \(t\) is the time in hours.
a.Write down the number of bacteria in the colony at time \(t = 0\).[1]
b.Calculate the number of bacteria present at 2 hours and 30 minutes. Give your answer correct to the nearest hundred bacteria.[3]
c.Calculate the time, in hours, for the number of bacteria to reach 5500.[2]
▶️Answer/Explanation
Markscheme
800 (A1) (C1)
\(800 \times {3^{(0.5 \times 2.5)}}\) (M1)
Note: Award (M1) for correctly substituted formula.
\( = 3158.57\)… (A1)
\(= 3200\) (A1) (C3)
Notes: Final (A1) is given for correctly rounding their answer. This may be awarded regardless of a preceding (A0).
\(5500 = 800 \times {3^{(0.5 \times t)}}\) (M1)
Notes: Award (M1) for equating function to 5500. Accept correct alternative methods.
\(= 3.51{\text{ hours}}\) (3.50968…) (A1) (C2)
Question
Consider the two functions, \(f\) and \(g\), where
\(f(x) = \frac{5}{{{x^2} + 1}}\)
\(g(x) = {(x – 2)^2}\)
a.Sketch the graphs of \(y = f(x)\) and \(y = g(x)\) on the axes below. Indicate clearly the points where each graph intersects the y-axis.
 [4]
[4]b.Use your graphic display calculator to solve \(f(x) = g(x)\).[2]
▶️Answer/Explanation
Markscheme
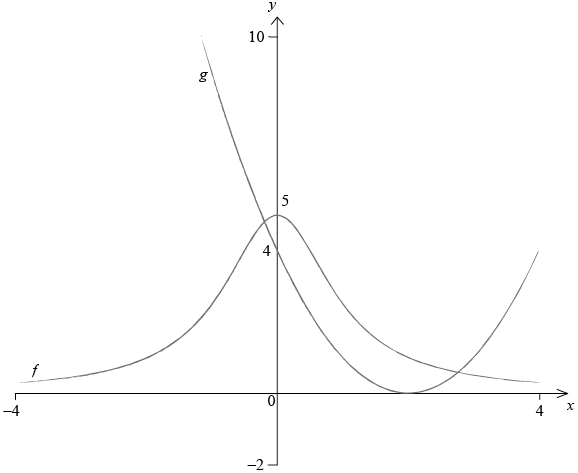
\(f(x)\): a smooth curve symmetrical about y-axis, \(f(x) > 0\) (A1)
Note: If the graph crosses the x-axis award (A0).
Intercept at their numbered \(y = 5\) (A1)
Note: Accept clear scale marks instead of a number.
\(g(x)\): a smooth parabola with axis of symmetry at about \(x = 2\) (the 2 does not need to be numbered) and \(g(x) \geqslant 0\) (A1)
Note: Right hand side must not be higher than the maximum of \(f(x)\) at \(x = 4\).
Accept the quadratic correctly drawn beyond \(x = 4\).
Intercept at their numbered \(y = 4\) (A1) (C4)
Note: Accept clear scale marks instead of a number.[4 marks]
\(–0.195, 2.76\) \((–0.194808…, 2.761377…)\) (A1)(ft)(A1)(ft) (C2)
Note: Award (A0)(A1)(ft) if both coordinates are given.
Follow through only if \(f(x) = \frac{5}{{{x^2}}} + 1\) is sketched; the solutions are \(–0.841, 3.22\) \((–0.840913…, 3.217747…)\)[2 marks]
