Question
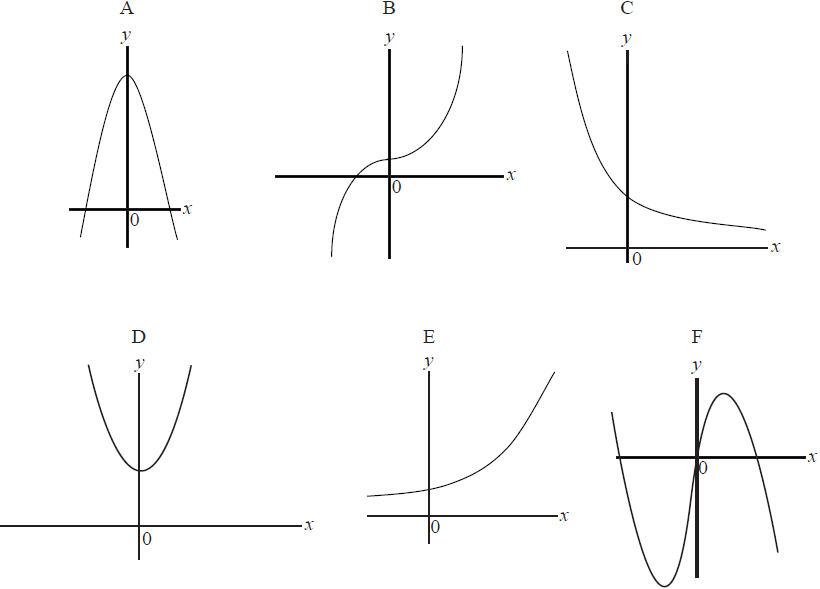
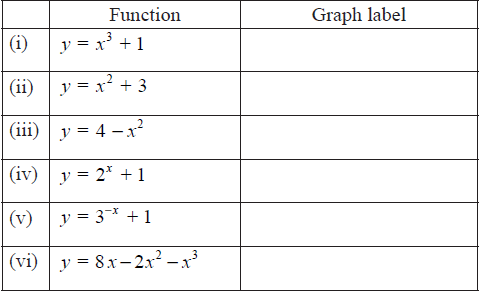
The following curves are sketches of the graphs of the functions given below, but in a different order. Using your graphic display calculator, match the equations to the curves, writing your answers in the table below.
(the diagrams are not to scale)
Answer/Explanation
Markscheme
(i) B (A1)
(ii) D (A1)
(iii) A (A1)
(iv) E (A1)
(v) C (A1)
(vi) F (A1) (C6)[6 marks]
Question
In an experiment it is found that a culture of bacteria triples in number every four hours. There are \(200\) bacteria at the start of the experiment.

Find the value of \(a\).[1]
Calculate how many bacteria there will be after one day.[2]
Find how long it will take for there to be two million bacteria.[3]
Answer/Explanation
Markscheme
\(a = 1800\) (A1) (C1)[1 mark]
\(200 \times {3^6}{\text{ (or }}16200 \times 9{\text{) }} = 145800\) (M1)(A1) (C2)[2 marks]
\(200 \times {3^n} = 2 \times {10^6}\) (where \(n\) is each \(4\) hour interval) (M1)
Note: Award (M1) for attempting to set up the equation or writing a list of numbers.
\({3^n} = {10^4}\)
\(n = 8.38{\text{ }}(8.383613097)\) correct answer only (A1)
\({\text{Time}} = 33.5{\text{ hours}}\) (accept \(34\), \(35\) or \(36\) if previous A mark awarded) (A1)(ft) (C3)
Note: (A1)(ft) for correctly multiplying their answer by \(4\). If \(34\), \(35\) or \(36\) seen, or \(32 – 36\) seen, award (M1)(A0)(A0).[3 marks]
Question
The number of cells, C, in a culture is given by the equation \(C = p \times 2^{0.5t} + q\), where t is the time in hours measured from 12:00 on Monday and p and q are constants.
The number of cells in the culture at 12:00 on Monday is 47.
The number of cells in the culture at 16:00 on Monday is 53.
Use the above information to write down two equations in p and q ;[2]
Use the above information to calculate the value of p and of q ;[2]
Use the above information to find the number of cells in the culture at 22:00 on Monday.[2]
Answer/Explanation
Markscheme
p + q = 47 (A1)
4p + q = 53 (A1) (C2)[2 marks]
Reasonable attempt to solve their equations (M1)
p = 2, q = 45 (A1) (C2)
Note: Accept only the answers p = 2, q = 45.[2 marks]
C = 2 × 20.5(10) + 45 (M1)
C = 109 (A1)(ft) (C2)
Note: Award (M1) for substitution of 10 into the formula with their values of p and q.[2 marks]
Question
Given the function \(f (x) = 2 \times 3^x\) for −2 \( \leqslant \) x \( \leqslant \) 5,
find the range of \(f\).[4]
find the value of \(x\) given that \(f (x) =162\).[2]
Answer/Explanation
Markscheme
\(f (-2) = 2 \times 3^{-2}\) (M1)
\(= \frac{{2}}{{9}}(0.222)\) (A1)
\(f (5) = 2 \times 3^5\)
\(= 486\) (A1)
\({\text{Range }}\frac{2}{9} \leqslant f(x) \leqslant 486\) OR \(\left[ {\frac{2}{9},{\text{ }}486} \right]\) (A1) (C4)
Note: Award (M1) for correct substitution of –2 or 5 into \(f (x)\), (A1)(A1) for each correct end point.[4 marks]
\(2 \times 3^x = 162\) (M1)
\(x = 4\) (A1) (C2)[2 marks]
Question
A rumour spreads through a group of teenagers according to the exponential model
\(N = 2 \times {(1.81)^{0.7t}}\)
where N is the number of teenagers who have heard the rumour t hours after it is first started.
Find the number of teenagers who started the rumour.[2]
Write down the number of teenagers who have heard the rumour five hours after it is first started.[1]
Determine the length of time it would take for 150 teenagers to have heard the rumour. Give your answer correct to the nearest minute.[3]
Answer/Explanation
Markscheme
N = 2 × (1.81)0.7×0 (M1)
N = 2 (A1) (C2)
Notes: Award (M1) for correct substitution of t = 0.
Award (A1) for correct answer.[2 marks]
16.0 (3 s.f) (A1) (C1)
Note: Accept 16 and 15.[1 mark]
150 = 2 × (1.81)0.7t (M1)
t = 10.39… h (A1)
t = 624 minutes (A1)(ft) (C3)
Notes: Accept 10 hours 24 minutes. Accept alternative methods.
Award last (A1)(ft) for correct rounding to the nearest minute of their answer.
Unrounded answer must be seen so that the follow through can be awarded.[3 marks]
