Home / IB Mathematics SL 3.3 Applications of right and non-right angled trigonometry AI SL Paper 2 – Exam Style Questions

IB Mathematics SL 3.3 Applications of right and non-right angled trigonometry AI SL Paper 2 - Exam Style Questions - New Syllabus

IB DP Maths AI SL Paper 2 - All Topics

Question 

The following diagram shows a park bounded by a fence in the shape of a quadrilateral ABCD. A straight path crosses through the park from B to D.
\(AB = 85\text{ m}\), \(AD = 85\text{ m}\), \(BC = 40\text{ m}\), \(\angle CB\hat{D}=41^\circ\), \(\angle BC\hat{D}=120^\circ\).
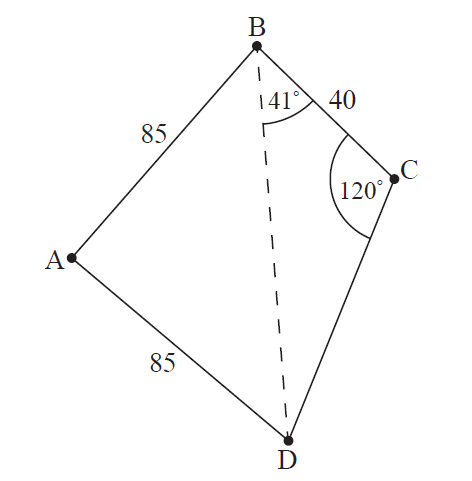
(a) (i) Write down the value of angle \(B\hat{D}C\).
     (ii) Hence use triangle \(BDC\) to find the length of path \(BD\). [4]
(b) Calculate the size of angle \(BA\hat{D}\), correct to five significant figures. [3]
The size of angle \(BA\hat{D}\) rounds to \(77^\circ\), correct to the nearest degree. Use \(BA\hat{D}=77^\circ\) for the rest of this question.
(c) Find the area bounded by the path \(BD\), and fences \(AB\) and \(AD\). [3]
A landscaping firm proposes a new design for the park. Fences \(BC\) and \(CD\) are to be replaced by a fence in the shape of a circular arc \(BED\) with centre \(A\). This is illustrated in the following diagram.
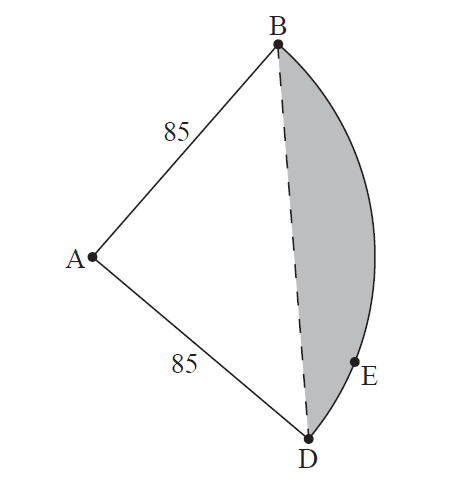
(d) Write down the distance from \(A\) to \(E\). [1]
(e) Find the perimeter of the proposed park, \(ABED\). [3]
(f) Find the area of the shaded region in the proposed park. [3]
▶️ Answer / Explanation
Solution

(a)

(i) In \(\triangle BDC\), angles sum to \(180^\circ\): \[ \angle BDC = 180^\circ – \angle CBD – \angle BCD = 180^\circ – 41^\circ – 120^\circ = \boxed{19^\circ}. \]
(ii) Sine rule in \(\triangle BDC\): \[ \frac{BD}{\sin 120^\circ}=\frac{BC}{\sin 19^\circ} \;\Rightarrow\; BD=40\cdot \frac{\sin 120^\circ}{\sin 19^\circ}. \] With \(\sin 120^\circ=\frac{\sqrt{3}}{2}\approx 0.866025\) and \(\sin 19^\circ\approx 0.325568\): \[ BD\approx 40\cdot \frac{0.866025}{0.325568}= \boxed{106.402\ \text{m}} \] (3 s.f.: \(106\) m).

(b)

Cosine rule in \(\triangle ABD\) (\(AB=AD=85\) m): \[ \cos(BA\hat{D})=\frac{85^2+85^2-BD^2}{2\cdot 85\cdot 85} =\frac{85^2+85^2-(106.4017\ldots)^2}{14450} =0.216517\ldots \] \[ \Rightarrow\ BA\hat{D}=\arccos(0.216517\ldots)=\boxed{77.495^\circ} \] (correct to five significant figures; use \(77^\circ\) in parts (c)–(f)).

(c)

Region is \(\triangle ABD\). Using included angle \(77^\circ\): \[ \text{Area}_{\triangle ABD} =\tfrac12\cdot 85\cdot 85\cdot \sin(77^\circ) =3519.91\ldots\ \text{m}^2 \;\Rightarrow\; \boxed{3\,520\ \text{m}^2}\ \text{(3 s.f.)}\]

(d)

Arc \(BED\) has centre \(A\) and radius \(AB=AD\). Hence \(\boxed{AE=85\ \text{m}}\).

(e)

Perimeter of \(ABED\) is straight sides \(AB+AD\) plus arc \(BD\) (central angle \(77^\circ\)): \[ P=85+85+\frac{77}{360}\cdot 2\pi(85) =170+\frac{77}{360}\cdot 170\pi \approx \boxed{284\ \text{m}} \] (unrounded total \(=284.232\ldots\ \text{m}\)).

(f)

Shaded area \(=\) sector \(A\) \((77^\circ,\ r=85)\) minus \(\triangle ABD\): \[ \text{Area}_{\text{sector}}=\frac{77}{360}\pi(85)^2=4854.85\ldots\ \text{m}^2, \]
\( \text{Shaded}=4854.85\ldots-3519.91\ldots=1334.94\ldots\ \text{m}^2 \;\Rightarrow\; \boxed{1\,335\ \text{m}^2}\ \text{(3 s.f.)}. \)
Total Marks: 17
More DP Math AI SL Paper 2 Questions..
Scroll to Top