Question 2 [Maximum mark: 15]
A farmer owns a field in the shape of a triangle ABC such that AB = 650 m, AC = 1005 m
and BC = 1225 m
diagram not to scale
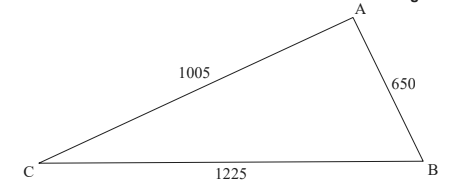
a. Find the size of AĈB. [3]
The local town is planning to build a highway that will intersect the borders of the field at points D and E, where DC = 210 m and CÊD = 100° , as shown in the diagram below.
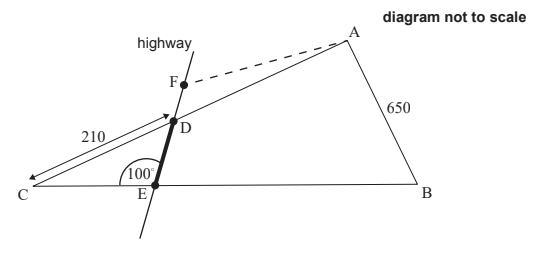
b. Find DE. [3]
The town wishes to build a carpark here. They ask the farmer to exchange the part of the field represented by triangle DCE. In return the farmer will get a triangle of equal area ADF, where F lies on the same line as D and E, as shown in the diagram above.
c. Find the area of triangle DCE. [5]
d. Estimate DF. You may assume the highway has a width of zero. [4]
Answer/Explanation
(a) cosine rule ACB = \(cos^{-1}(\frac{1005^{2}+1225^{2}-650^{2}}{2\times 1005\times 1225})\)
\(= 32.0 ((31.9980…)\) OR \(0.558 (0.558471…)\)
(b) sine rule \(\frac{DE}{sin31.9980..}= \frac{210}{sin100}\)
\(DE = 113 m (112.9937…)\)
(c) \(180-(100 +their part (a))=48.0019\) OR
\(0.837791…\(\frac{1}{2}\times 112.9937…\times 210\times sin48.002\)
\(8820m^{2}\rightarrow (8817.18 )\)
(d) \(1005 − 210 \) OR \(795\)
equating answer to part (c) to area of a triangle formula
\(8817.18..=\frac{1}{2}\times DF\times (1005-210)\times sin48.002..\)
\((DF=)29.8m(29.8473….)\)
Question 2. [Maximum mark: 17]
The diagram below shows a circular clock face with centre O. The clock’s minute hand has a length of 10 cm. The clock’s hour hand has a length of 6 cm.
At 4:00 pm the endpoint of the minute hand is at point A and the endpoint of the hour hand is at point B.
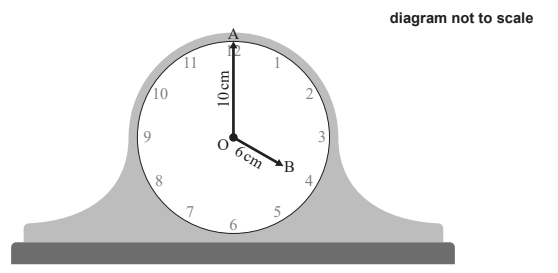
a. Find the size of angle AÔB in degrees. [2]
b. Find the distance between points A and B. [3]
Between 4:00 pm and 4:13 pm, the endpoint of the minute hand rotates through an angle, θ ,
from point A to point C. This is illustrated in the diagram.

c. Find the size of angle θ in degrees. [2]
d. Calculate the length of arc AC. [2]
e. Calculate the area of the shaded sector, AOC. [2]
A second clock is illustrated in the diagram below. The clock face has radius 10 cm with minute and hour hands both of length 10 cm. The time shown is 6:00 am. The bottom of the clock face is located 3 cm above a horizontal bookshelf.
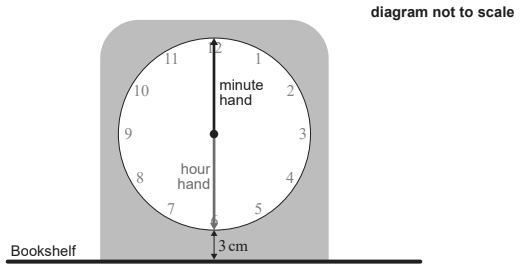
Write down the height of the endpoint of the minute hand above the bookshelf
at 6:00 am. [1]
f. The height, h centimetres, of the endpoint of the minute hand above the bookshelf is modelled by the function
h(θ ) = 10 cosθ + 13 , θ ≥ 0 ,
where θ is the angle rotated by the minute hand from 6:00 am.
g. Find the value of h when θ = 160° . [2]
The height, g centimetres, of the endpoint of the hour hand above the bookshelf is modelled by the function
g(θ ) = -10 cos \((\frac{\Theta }{12})\) + 13 , θ ≥ 0 ,
where θ is the angle in degrees rotated by the minute hand from 6:00 am.
h. Write down the amplitude of g(θ ) . [1]
The endpoints of the minute hand and hour hand meet when θ = k .
Find the smallest possible value of k . [2]
Answer/Explanation
(a) \(4\times \frac{360°\cdot }{12}OR 4\times 30° = 120°\)
(b) cosine rule \(AB^{2}= 10^{2}+6^{2}-2\times 10\times 6\times cos (120°)\)
\(AB= 14cm\)
(c) \(\Theta = 13\times 6= 78°\)
(d) arc length l= \(\frac{78}{360} \times 2\times \pi \times 10\) OR
\(l= \frac{13\pi }{30}\times 10 = 13.6cm(13.6135…,4.33\pi ,\frac{13\pi }{3})\)
(e) Area of a sector \(A= \frac{78}{360}\times \pi \times 10^{2}\) OR \( l=\frac{1}{2}\times \frac{13\pi }{30}\times 10^{2}= 68.1cm^{2}(68.0678…,21.7\pi ,\frac{65\pi }{3}\)
(f) 23
(g) correct substitution h =10cos (160 ) + 13 = 3.60 cm (3.60307…)
(h) 10 (i) EITHER 10\(\times cos(\Theta )+13 = -10\times cos(\frac{\Theta }{12})\)+13
OR  THEN k =196° (196.363…)
THEN k =196° (196.363…)
Question
A sector of a circle, centre O and radius 4.5m, is shown in the following diagram.
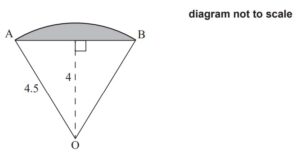
(a) (i) Find the angle AÔB.
(ii) Find the area of the shaded segment. [8]
A square field with side 8m has a goat tied to a post in the centre by a rope such that the
goat can reach all parts of the field up to 4.5m from the post.
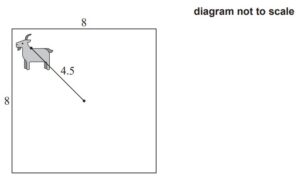
(b) (i) Find the area of a circle with radius 4.5m.
(ii) Find the area of the field that can be reached by the goat. [5]
Let V be the volume of grass eaten by the goat, in cubic metres, and t be the length of time,
in hours, that the goat has been in the field.
The goat eats grass at the rate of \(\frac{dV}{dt}=0.3te^{-t}\).
(c) Find the value of t at which the goat is eating grass at the greatest rate. [2]
Answer/Explanation
Ans
4. (a) (i) \(\left ( \frac{1}{2}A\hat{O}B= \right )\arccos \left ( \frac{4}{4.5} \right )=27.266…\) (M1)(A1)
AOB 54.532… ≈ 54.5 o = ( 0.951764…≈ 0.952 radians) A1
Note: Other methods may be seen; award (M1)(A1) for use of a correct trigonometric
method to find an appropriate angle and then A1 for the correct answer.
(ii) finding area of triangle
EITHER
area of triangle \(=\frac{1}{2}\times 4.5^{2}\times \sin (54.532…)\) (M1)
Note: Award M1 for correct substitution into formula.
= 8.24621…≈ 8.25 m2
OR
\(AB=2\times \sqrt{4.5^{2}-4^{2}}=4.1231…\) (M1)
\(area\ triangle=\frac{4.12131…\times 4}{2}\) (A1)
= 8.24621…≈ 8.25 m2
EITHER
\(area\ of \ sector=\frac{54.532…}{360}\times \pi \times 4.5^{2}\) (M1)
= 9.63661… ≈ 9.64 m2
OR
\(area\ of \ sector=\frac{1}{2}\times 0.9517641.. \times 4.5^{2}\) (M1)
= 9.63661… ≈ 9.64 m2 (A1)
THEN
area of segment = 9.63661… 8.24621… −
=1.39 m2 (1.39040…) A1
[8 marks]
(b) (i) 2 π× 4.5 (M1)
63.6 m2 (63.6172… m2 ) A1
(ii) METHOD 1
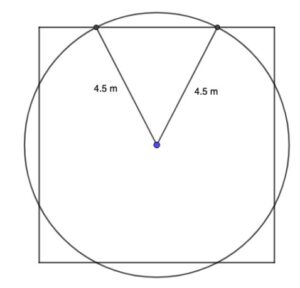
4 1.39040… × (5.56160) (A1)
subtraction of four segments from area of circle (M1)
= 58.1 m2 (58.055…) A1
METHOD 2
\(4(0.5\times 4.5^{2} \times\sin 54.532… )+4\left ( \frac{35.4679}{360}\times\pi \times 4.5^{2} \right )\) (M1)
= 32.9845… + 25.0707 (A1)
= 58.1 m2 (58.055 …) A1
[5 marks]
(c) sketch of \(\frac{dV}{dt}\) OR \(\frac{dV}{dt}=0.110363…\) OR attempt to find where \(\frac{d^{2}V}{dt^{2}}=0\) (M1)
t =1 hour A1
[2 marks]
[Total 15 marks]
Question
The quadrilateral ABCD shown below represents a sandbox. AB and BC have the same length. AD is \(9{\text{ m}}\) long and CD is \(4.2{\text{ m}}\) long. Angles ADC and ABC are \({95^ \circ }\) and \({130^ \circ }\) respectively.
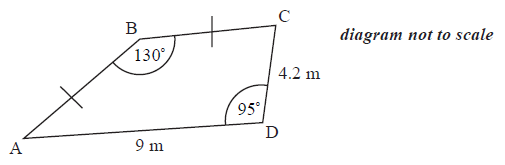
Find the length of AC.[3]
(i) Write down the size of angle BCA.
(ii) Calculate the length of AB.[4]
Show that the area of the sandbox is \(31.1{\text{ }}{{\text{m}}^2}\) correct to 3 s.f.[4]
The sandbox is a prism. Its edges are \(40{\text{ cm}}\) high. The sand occupies one third of the volume of the sandbox. Calculate the volume of sand in the sandbox.[3]
Answer/Explanation
Markscheme
\({\text{A}}{{\text{C}}^2} = {9^2} + {4.2^2} – 2 \times 9 \times 4.2 \times \cos {95^ \circ }\) (M1)(A1)
\({\text{AC}} = 10.3{\text{ m}}\) (A1)(G2)
Note: (M1) for correct substituted formula and (A1) for correct substitution. If radians used answer is \(6.59\). Award at most (M1)(A1)(A0).
Note: The final A1 is only awarded if the correct units are present; only penalize once for the lack of units or incorrect units.
(i) \({\text{B}}\hat{\text{C}}{\text{A}} = {25^ \circ }\) (A1)
(ii) \(\frac{{{\text{AB}}}}{{\sin {{25}^ \circ }}} = \frac{{10.258 \ldots }}{{\sin {{130}^ \circ }}}\) (M1)(A1)
\({\text{AB}} = 5.66{\text{ m}}\) (A1)(ft)(G2)
Note: (M1) for correct substituted formula and (A1) for correct substitution. (A1) for correct answer.
Follow through with angle \({\text{B}}\)\(\hat{\text{C}}\)\({\text{A}}\) and their AC. Allow \({\text{AB}} = 5.68\) if \({\text{AC}} = 10.3\) used. If radians used answer is \(0.938\) (unreasonable answer). Award at most (M1)(A1)(A0)(ft).
OR
Using that ABC is isosceles
\({\text{cos2}}{{\text{5}}^ \circ } = \frac{{\frac{1}{2} \times 10.258 \ldots }}{{{\text{AB}}}}\) (or equivalent) (A1)(M1)(ft)
\({\text{AB}} = 5.66{\text{ m}}\) (A1)(ft)(G2)
Note: (A1) for \(\frac{1}{2}\) of their AB seen, (M1) for correct trigonometric ratio and correct substitution, (A1) for correct answer. If \(\frac{1}{2}{\text{AB}}\) seen and correct answer is given award (A1)(G1). Allow \({\text{AB}} = 5.68\) if \({\text{AC}} = 10.3\) used. If radians used answer is \(3.32\). Award (A1)(M1)(A1)(ft). If \(\sin 65\) and radians used answer is \(3.99\). Award (A1)(M1)(A1)(ft).
Note: The final A1 is only awarded in (ii) if the correct units are present; only penalize once for the lack of units or incorrect units.
Area \( = \frac{1}{2} \times 9 \times 4.2 \times \sin {95^ \circ } + \frac{1}{2} \times {(5.6592 \ldots )^2} \times \sin {130^ \circ }\) (M1)(M1)(ft)(M1)
\( = 31.095 \ldots = 31.1{\text{ }}{{\text{m}}^2}\) (correct to 3 s.f.) (A1)(AG)
Note: (M1)(M1) each for correct substitution in the formula of the area of each triangle, (M1) for adding both areas. (A1) for unrounded answer. Follow through with their length of AB but last mark is lost if they do not reach the correct answer.
Volume of sand \( = \frac{1}{3}(31.09 \ldots \times 0.4)\) (M1)(M1)
\( = 4.15{\text{ }}{{\text{m}}^3}\) (A1)(G2)
Note: (M1) for correct formula of volume of prism and for correct substitution, (M1) for multiplying by \(\frac{1}{3}\) and last (A1) for correct answer only.
Note: The final A1 is only awarded if the correct units are present; only penalize once for the lack of units or incorrect units.
