Question 1 [Maximum mark: 15]
A farmer owns a field in the shape of a triangle ABC such that AB = 650 m, AC = 1005 m
and BC = 1225 m
diagram not to scale
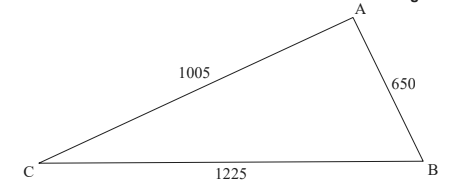
a. Find the size of AĈB. [3]
The local town is planning to build a highway that will intersect the borders of the field at points D and E, where DC = 210 m and CÊD = 100° , as shown in the diagram below.
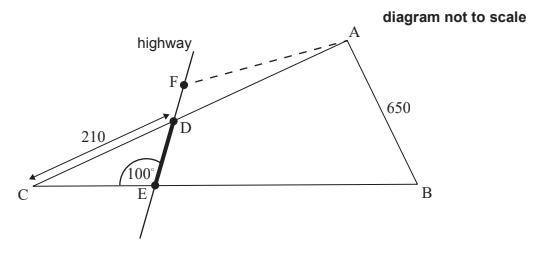
b. Find DE. [3]
The town wishes to build a carpark here. They ask the farmer to exchange the part of the field represented by triangle DCE. In return the farmer will get a triangle of equal area ADF, where F lies on the same line as D and E, as shown in the diagram above.
c. Find the area of triangle DCE. [5]
d. Estimate DF. You may assume the highway has a width of zero. [4]
▶️Answer/Explanation
(a) cosine rule ACB = \(cos^{-1}(\frac{1005^{2}+1225^{2}-650^{2}}{2\times 1005\times 1225})\)
\(= 32.0 ((31.9980…)\) OR \(0.558 (0.558471…)\)
(b) sine rule \(\frac{DE}{sin31.9980..}= \frac{210}{sin100}\)
\(DE = 113 m (112.9937…)\)
(c) \(180-(100 +their part (a))=48.0019\) OR
\(0.837791…\(\frac{1}{2}\times 112.9937…\times 210\times sin48.002\)
\(8820m^{2}\rightarrow (8817.18 )\)
(d) \(1005 − 210 \) OR \(795\)
equating answer to part (c) to area of a triangle formula
\(8817.18..=\frac{1}{2}\times DF\times (1005-210)\times sin48.002..\)
\((DF=)29.8m(29.8473….)\)
Question 6. [Maximum mark: 18]
An ice-skater is skating such that her position vector when viewed from above at time t
seconds can be modelled by
\((_{x}^{y})\) = 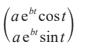
with respect to a rectangular coordinate system from a point O, where the non-zero constants a and b can be determined. All distances are in metres.
a. Find the velocity vector at time t . [3]
b. Show that the magnitude of the velocity of the ice-skater at time t is given by
\(a^{ebt}\sqrt{(1+b^{2})}\) [4]
At time t = 0 , the displacement of the ice-skater is given by \((_{0}^{5})\) and the velocity of the
ice-skater is given by ( 5 ) .
c. Find the value of a and the value of b . [3]
d. Find the magnitude of the velocity of the ice-skater when t = 2 . [2] At a point P, the ice-skater is skating parallel to the y-axis for the first time.
e. Find OP. [6]
▶️Answer/Explanation
(a) use of product rule \((_{y}^{x})= (_{abe^{bt}sin t + ae^{bt}cost t}^{abe ^{bt}cost – ae ^{bt}sin t})\)
(b) \(|v|^{2}= x^{2}+y^{2}=[abe^{bt}cost – ae^{bt}sint]^{2}+ [abe^{bt}sint+ae^{bt}cost]^{2}\)
\(= [a^{2}sin^{2}t – 2a^{2}bsin t cost + a^{2}b^{2}cos^{2}t + a^{2}cos^{2}+ 2a^{2}bsint costt +a^{2}b^{2}sin^{2}t ]\) use of \(sin^{2}t + cos^{2}t=1\)
\(=a^{2}(b^{2}+1)e^{2bt}\) magnitude of velocity is \(ae^{bt}\sqrt{(1+ b^{2})}\)
(c) when t = 0, \(ae^{bt}cost = 5 a=5 abe^{bt}cost – ae^{bt}sint = -3.5 b = -0.7\ )
(d)\(5e^{-0.7\times 2}\sqrt{(1+(-0.7)^{2})}1.51(1.50504…)\)
(e) \(x=0 ae^{bt}(b cost – simt)=0 tant=b t = 2.53 (2.53086…)\) correct substitution of their t to find x or y
\(x = − 0.697 (- 0.696591…)\) and \(y = 0.488 (0.487614…)\)
use of Pythagoras / distance formula \(OP = 0.850 m (0.850297…)\)
Question
A sector of a circle, centre O and radius 4.5m, is shown in the following diagram.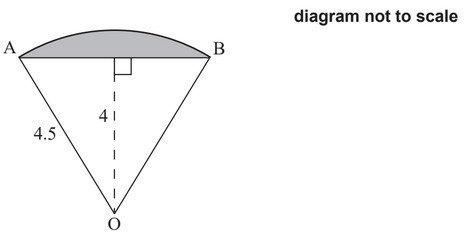
(a) (i) Find the angle AÔB.
(ii) Find the area of the shaded segment.
A square field with side 8m has a goat tied to a post in the centre by a rope such that the
goat can reach all parts of the field up to 4.5m from the post.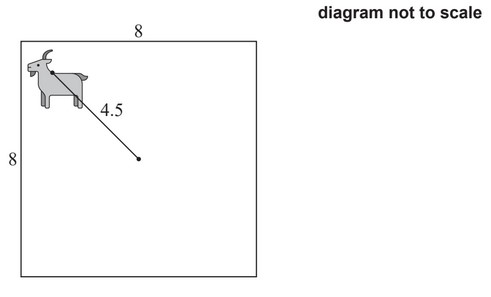
(b) Find the area of the field that can be reached by the goat.
Let V be the volume of grass eaten by the goat, in cubic metres, and t be the length of time,
in hours, that the goat has been in the field.
The goat eats grass at the rate of \(\frac{dV}{dt}=0.3te^{-t}\).
(c) Find the value of t at which the goat is eating grass at the greatest rate.
The goat is tied in the field for 8 hours.
(d) Find the total volume of grass eaten by the goat during this time.
▶️Answer/Explanation
Ans:


Question
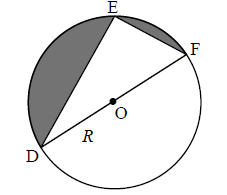
A new triangle DEF is positioned within a circle radius R such that DF is a diameter as shown in the following diagram.
a.i.In a triangle ABC, prove \(\frac{a}{{{\text{sin}}\,A}} = \frac{b}{{{\text{sin}}\,B}} = \frac{c}{{{\text{sin}}\,C}}\).[4]
a.ii.Prove that the area of the triangle ABC is \(\frac{1}{2}ab\,{\text{sin}}\,{\text{C}}\).[2]
a.iii.Given that R denotes the radius of the circumscribed circle prove that \(\frac{a}{{{\text{sin}}\,A}} = \frac{b}{{{\text{sin}}\,B}} = \frac{c}{{{\text{sin}}\,C}} = 2R\).[2]
a.iv.Hence show that the area of the triangle ABC is \(\frac{{abc}}{{4R}}\).[2]
b.i.Find in terms of R, the two values of (DE)2 such that the area of the shaded region is twice the area of the triangle DEF.[9]
b.ii.Using two diagrams, explain why there are two values of (DE)2.[2]
c.A parallelogram is positioned inside a circle such that all four vertices lie on the circle. Prove that it is a rectangle.[3]
▶️Answer/Explanation
Markscheme
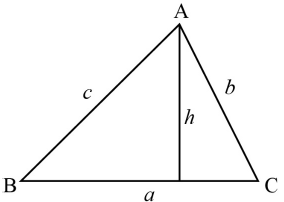
\({\text{sin}}\,{\text{B}} = \frac{h}{c}\) and \({\text{sin}}\,{\text{C}} = \frac{h}{b}\) M1A1
hence \(h = c\,{\text{sin}}\,{\text{B}} = b\,{\text{sin}}\,{\text{C}}\) A1
by dropping a perpendicular from B, in exactly the same way we find \(c\,{\text{sin}}\,{\text{A}} = a\,{\text{sin}}\,{\text{C}}\) R1
hence \(\frac{a}{{{\text{sin}}\,A}} = \frac{b}{{{\text{sin}}\,B}} = \frac{c}{{{\text{sin}}\,C}}\)
[4 marks]
area = \(\frac{1}{2}ah\) M1A1
= \(\frac{1}{2}ab\,{\text{sin}}\,{\text{C}}\) AG
[2 marks]

since the angle at the centre of circle is twice the angle at the circumference \({\text{sin}}\,A = \frac{a}{{2R}}\) M1A1
hence \(\frac{a}{{{\text{sin}}\,A}} = 2R\) and therefore \(\frac{a}{{{\text{sin}}\,A}} = \frac{b}{{{\text{sin}}\,B}} = \frac{c}{{{\text{sin}}\,C}} = 2R\) AG
[2 marks]
area of the triangle is \(\frac{1}{2}ab\,{\text{sin}}\,{\text{C}}\) M1
since \({\text{sin}}\,{\text{C}} = \frac{c}{{2R}}\) A1
area of the triangle is \(\frac{1}{2}ab\,\frac{c}{{2R}} = \frac{{abc}}{{4R}}\) AG
[2 marks]
area of the triangle is \(\frac{{\pi {R^2}}}{6}\) (M1)A1
(DE)2 + (EF)2 = 4R2 M1
(DE)2 = 4R2 − (EF)2
\(\frac{1}{2}\left( {{\text{DE}}} \right)\left( {{\text{EF}}} \right) = \frac{{\pi {R^2}}}{6} \Rightarrow \left( {{\text{EF}}} \right) = \frac{{\pi {R^2}}}{{3\left( {{\text{DE}}} \right)}}\) M1A1
\({\left( {{\text{DE}}} \right)^2} = 4{R^2} – \frac{{{\pi ^2}{R^4}}}{{9{{\left( {{\text{DE}}} \right)}^2}}}\) A1
\(9{\left( {{\text{DE}}} \right)^4} – 36{\left( {{\text{DE}}} \right)^2}{R^2} + {\pi ^2}{R^4} = 0\) A1
\({\left( {{\text{DE}}} \right)^2} = \frac{{36{R^2} \pm \sqrt {1296{R^4} – 36{\pi ^2}{R^4}} }}{{18}}\) M1
\({\left( {{\text{DE}}} \right)^2} = \frac{{36{R^2} \pm 6{R^2}\sqrt {36 – {\pi ^2}} }}{{18}}\left( { = \frac{{6{R^2} \pm {R^2}\sqrt {36 – {\pi ^2}} }}{3}} \right)\) A1
[9 marks]
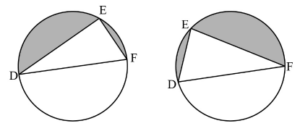 A1A1
A1A1
[2 marks]
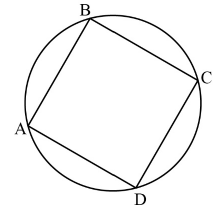
\(\mathop {\text{A}}\limits^ \wedge + \mathop {\text{C}}\limits^ \wedge = 180^\circ \) (cyclic quadrilateral) R1
however \(\mathop {\text{A}}\limits^ \wedge = \mathop {\text{C}}\limits^ \wedge \) (ABCD is a parallelogram) R1
\(\mathop {\text{A}}\limits^ \wedge = \mathop {\text{C}}\limits^ \wedge = 90^\circ \) A1
\(\mathop {\text{B}}\limits^ \wedge = \mathop {\text{D}}\limits^ \wedge = 90^\circ \)
hence ABCD is a rectangle AG
[3 marks]
Question
The area of an equilateral triangle is \(1\) cm2. Determine the area of:
The points A, B have coordinates (\(1\), \(0\)), (\(0\), \(1\)) respectively. The point P(\(x\), \(y\)) moves in such a way that \({\rm{AP}} = k{\rm{BP}}\) where \(k \in {\mathbb{R}^ + }\) .
A.a.the circumscribed circle.[8]
A.b.the inscribed circle.[3]
B.a.When \(k = 1\) , show that the locus of P is a straight line.[3]
B.b.When \(k \ne 1\) , the locus of P is a circle.
(i) Find, in terms of \(k\) , the coordinates of C, the centre of this circle.
(ii) Find the equation of the locus of C as \(k\) varies.[9]
▶️Answer/Explanation
Markscheme
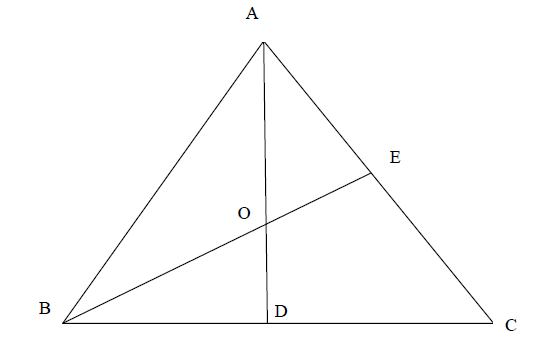
consider the above diagram – [AD] and [BE] are the medians and O is therefore both the incentre and the circumcentre (R1)
let \({\rm{AB}} = d\) and let \(R\) denote the radius of the circumcircle
then,
\(R = {\rm{AO}} = {\rm{AE}}\sec {30^ \circ }\) M1
\( = \frac{d}{2} \times \frac{2}{{\sqrt 3 }} = \frac{d}{{\sqrt 3 }}\) (A1)
area of circumcircle \( = \pi {R^2} = \frac{{\pi {d^2}}}{3}\) A1
area of triangle \({\rm{ = }}\frac{{\rm{1}}}{{\rm{2}}}{\rm{AB}}{\rm{.AC}}\sin {\rm{BAC}}\) M1
\( = \frac{{\sqrt 3 {d^2}}}{4}\) (A1)
\(\frac{{\sqrt 3 {d^2}}}{4} = 1 \Rightarrow {d^2} = \frac{4}{{\sqrt 3 }}\) A1
area of circumcircle \( = \frac{{4\pi }}{{3\sqrt 3 }}\) (\(2.42\)) A1
[8 marks]
let \(r\) denote the radius of the incircle
then
\(r = {\rm{OE}} = {\rm{AE}}\tan {30^ \circ }\) M1
\( = \frac{d}{{2\sqrt 3 }}\) (A1)
area of incircle \( = \pi {r^2} = \frac{{\pi {d^2}}}{{12}}\)
\( = \frac{\pi }{{3\sqrt 3 }}\) (\(0.605\)) A1
[3 marks]
\({\rm{A}}{{\rm{P}}^2} = {(x – 1)^2} + {y^2}\) and \({\rm{B}}{{\rm{P}}^2} = {x^2} + {(y – 1)^2}\) A1
\({x^2} – 2x + 1 + {y^2} = {x^2} + {y^2} – 2y + 1\) M1
\(y = x\) which is the equation of a straight line A1
[3 marks]
(i) \({x^2} – 2x + 1 + {y^2} = {k^2}({x^2} + {y^2} – 2y + 1)\) M1
\(({k^2} – 1){x^2} + ({k^2} – 1){y^2} + 2x – 2{k^2}y + {k^2} – 1 = 0\) A1
\({x^2} + {y^2} + \frac{{2x}}{{{k^2} – 1}} – \frac{{2{k^2}y}}{{{k^2} – 1}} + 1 = 0\) A1
by completing the squares or quoting the standard result, M1
coordinates of C are
\(\left( { – \frac{1}{{{k^2} – 1}},\frac{{{k^2}}}{{{k^2} – 1}}} \right)\) A1
(ii) let (\(x\), \(y\)) be the coordinates of C
attempting to find \(k\) or \({{k^2}}\) , (M1)
\({k^2} = 1 – \frac{1}{x}\) (A1)
\(y = \frac{{1 – \frac{1}{x}}}{{ – \frac{1}{x}}}\) (M1)
\(y = 1 – x\) A1
[9 marks]
