Question
A student investigating the relationship between chemical reactions and temperature finds
the Arrhenius equation on the internet.
\(k=Ae^{-\frac{c}{T}}\)
This equation links a variable k with the temperature T, where A and c are positive
constants and T > 0.
(a) Show that \(\frac{dk}{dT}\) is always positive. [3]
(b) Given that \(\lim_{T\rightarrow \infty }k=A \ and \ \lim_{T\rightarrow 0}k=0\), sketch the graph of k against T. [3]
The Arrhenius equation predicts that the graph of ln k against \(\frac{1}{T}\) is a straight line.
(c) Write down
(i) the gradient of this line in terms of c ;
(ii) the y-intercept of this line in terms of A. [4]
The following data are found for a particular reaction, where T is measured in Kelvin
and k is measured in cm3 mol−1 s−1:
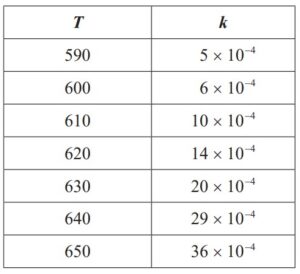
(d) Find the equation of the regression line for ln k on \(\frac{1}{T}\) [2]
(e) Find an estimate of
(i) c ;
(ii) A.
It is not required to state units for these values. [3]
▶️Answer/Explanation
Ans
4. (a) attempt to use chain rule, including the differentiation of \(\frac{1}{T}\) (M1)
\(\frac{dk}{dT}=A\times \frac{c}{T^{2}}\times e^{-\frac{c}{T}}\)
this is the product of positive quantities so must be positive R1
Note: The R1 may be awarded for correct argument from their derivative.
R1 is not possible if their derivative is not always positive.
[3 marks]
(b)
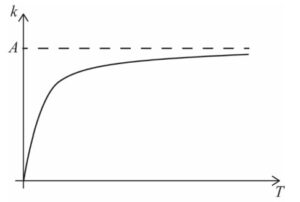
A1A1A1
Note: Award A1 for an increasing graph, entirely in first quadrant, becoming
concave down for larger values of T, A1 for tending towards the origin
and A1 for asymptote labelled at k = A .
[3 marks]
(c) taking ln of both sides OR substituting y = ln x and \(x=\frac{1}{T}\) (M1)
\(ln k=ln A=-\frac{c}{T}\ OR \ y=-cx+ln A\) (A1)
(i) so gradient is −c A1
(ii) y-intercept is ln A A1
Note: The implied (M1) and (A1) can only be awarded if both correct answers are
seen. Award zero if only one value is correct and no working is seen.
[4 marks]
continued…
(d) an attempt to convert data to \(\frac{1}{T}\) ln k (M1)
e.g. at least one correct row in the following table
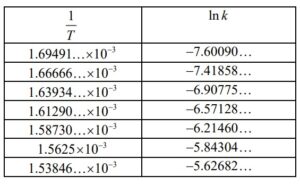
line is \(ln k=-13400\times \frac{1}{T}+15.0 \left ( =-13383.1…\times \frac{1}{T}+15.0107 \right )\) A1
[2 marks]
(e) (i) c =13400 (13383.1 ) … A1
(ii) attempt to rearrange or solve graphically ln 15.0107 A = … (M1)
A = (3300000 3304 258…) A1
Note: Accept an A value of 3269017… from use of 3sf value.
[3 marks]
Total [15 marks]
Question
The scores of the eight highest scoring countries in the 2019 Eurovision song contest are
shown in the following table.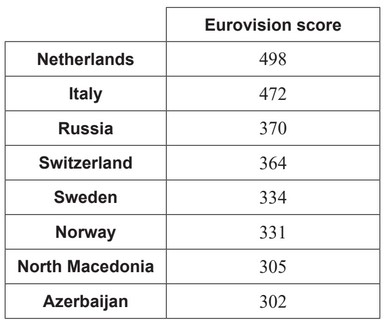
(a) For this data, find
(i) the upper quartile.
(ii) the interquartile range.
(b) Determine if the Netherlands’ score is an outlier for this data. Justify your answer.
Chester is investigating the relationship between the highest-scoring countries’ Eurovision
score and their population size to determine whether population size can reasonably be
used to predict a country’s score.
The populations of the countries, to the nearest million, are shown in the table.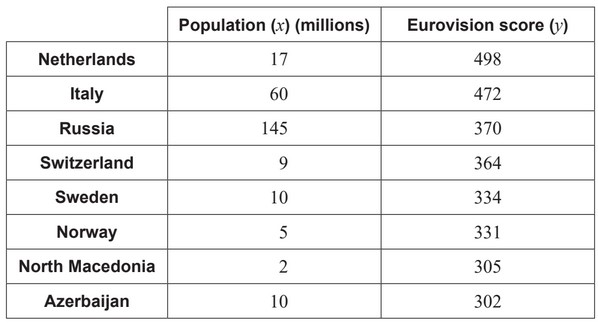
Chester finds that, for this data, the Pearson’s product moment correlation coefficient
is r = 0.249.
(c) State whether it would be appropriate for Chester to use the equation of a regression
line for y on x to predict a country’s Eurovision score. Justify your answer.
Chester then decides to find the Spearman’s rank correlation coefficient for this data,
and creates a table of ranks.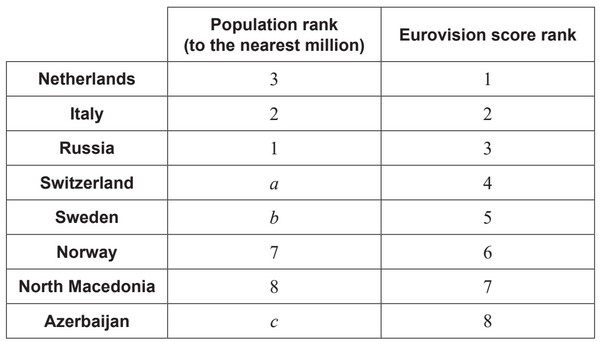
(d) Write down the value of:
(i) a ,
(ii) b ,
(iii) c .
(e) Find the value of the Spearman’s rank correlation coefficient \(r_s\).
(ii) Interpret the value obtained for \(r_S\).
(f) When calculating the ranks, Chester incorrectly read the Netherlands’ score as 478. Explain why the value of the Spearman’s rank correlation \(r_S\) does not change despite this error.
▶️Answer/Explanation
Ans:
(a) (i) \(\frac{370+472}{2}\)
\(Q_3 = 421\)
(ii) their part (a)(i) – their \(Q_1\) (clearly stated)
IQR = (421 – 318=) 103
(b) \((Q_3 + 1.5(IQR)=) 421 + (1.5 \(\times 103)\)
= 575.5
since 498 < 575.5
Netherlands is not an outlier
(c) not apptopriate (“no” no sufficient)
as r is too close to zero / too weak a correlation
(d) (i) 6
(ii) 4.5
(iii)4.5
(e) (i) \(r_s = 0.683 (0.682646…)\)
(ii) EITHER
there is a (positive) association between the population size and the score
OR
there is a (positive) linear correlation between the ranks of the population size
and the ranks of the scores (when compared with the PMCC of 0.249)
(f) lowering the top score by 20 does not change its rank so \(r_S\) is unchanged.
Question
Jim is investigating the relationship between height and foot length in teenage boys.
A sample of 13 boys is taken and the height and foot length of each boy are measured.
The results are shown in the table.
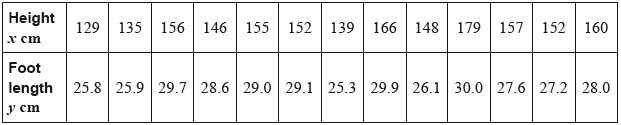
You may assume that this is a random sample from a bivariate normal distribution.
Jim wishes to determine whether or not there is a positive association between height and foot length.
a.Calculate the product moment correlation coefficient.[2]
b.Find the \(p\)–value.[2]
c.Interpret the \(p\)–value in the context of the question.[1]
d.Find the equation of the regression line of \(y\) on \(x\).[2]
e.Estimate the foot length of a boy of height 170 cm.[2]
▶️Answer/Explanation
Markscheme
Note: In all parts accept answers which round to the correct 2sf answer.
\(r = 0.806\) A2
\(4.38 \times {10^{ – 4}}\) A2
\(p\)-value represents strong evidence to indicate a (positive) association between height and foot length A1
Note: FT the \(p\)-value
\(y = 0.103x + 12.3\) A2
attempted substitution of \(x = 170\) (M1)
\(y = 29.7\) A1
Note: Accept \(y = 29.8\)
