Question 10. [Maximum mark: 7]
A game is played where two unbiased dice are rolled and the score in the game is the greater of the two numbers shown. If the two numbers are the same, then the score in the game is the number shown on one of the dice. A diagram showing the possible outcomes is given below.
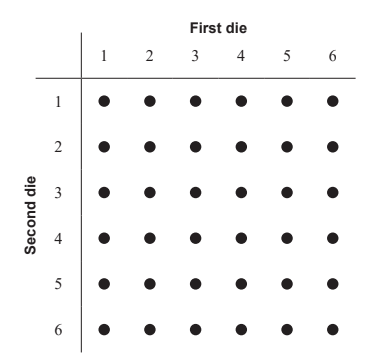
Let T be the random variable “the score in a game”.
(a) Complete the table to show the probability distribution of T . [2]
t | 1 | 2 | 3 | 4 | 5 | 6 |
P(T = t) |
(b) Find the probability that
(i)a player scores at least 3 in a game.
(ii) a player scores 6, given that they scored at least 3. [3]
()Find the expected score of a game. [2]
▶️Answer/Explanation
(a) 
(b) (i) \(\frac{32}{36}(\frac{8}{9},0.888888…, 88.9%)\)
(ii) use of conditional probability \(\frac{11}{32}\) (0.34375,34.4%)
(c)\(\frac{1 \times 1+3\times 2+5\times 3+…+11\times 6}{36}= \frac{161}{36}(4.4477222…)\)
Question 8. [Maximum mark: 7]
A game is played where two unbiased dice are rolled and the score in the game is the greater of the two numbers shown. If the two numbers are the same, then the score in the game is the number shown on one of the dice. A diagram showing the possible outcomes is given below.

Let T be the random variable “the score in a game”.
(a) Complete the table to show the probability distribution of T . [2]
t | 1 | 2 | 3 | 4 | 5 | 6 |
P(T = t) |
(b) Find the probability that
(i)a player scores at least 3 in a game.
(ii) a player scores 6, given that they scored at least 3. [3]
()Find the expected score of a game. [2]
▶️Answer/Explanation
(a) 
- Note: Award A1 if three to five probabilities are correct. (b) (i) \(\frac{32}{36}(\frac{8}{9},0.888888…, 88.9%)\) (ii) use of conditional probability \(\frac{11}{32}\) (0.34375,34.4%) (c)\(\frac{1 \times 1+3\times 2+5\times 3+…+11\times 6}{36}= \frac{161}{36}(4.4477222…)\)
- e.g. denominator of 32
Question
A polygraph test is used to determine whether people are telling the truth or not, but it is not
completely accurate. When a person tells the truth, they have a 20% chance of failing the test.
Each test outcome is independent of any previous test outcome.
10 people take a polygraph test and all 10 tell the truth.
(a) Calculate the expected number of people who will pass this polygraph test.
(b) Calculate the probability that exactly 4 people will fail this polygraph test.
(c) Determine the probability that fewer than 7 people will pass this polygraph test.
▶️Answer/Explanation
Ans:
(a) \((E(X)=)10 \times 0.8\)
8 (people)
(b) recognition of binomial probability
0.0881 (0.0880803…)
(c) 0.8 and 6 seen OR 0.2 and 3 seen
attempt to use binomial probability
0.121 (0.120873…)
Question
A group of 130 applicants applied for admission into either the Arts programme or the Sciences
programme at a university. The outcomes of their applications are shown in the following table.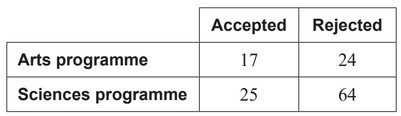
(a) Find the probability that a randomly chosen applicant from this group was accepted by
the university.
An applicant is chosen at random from this group. It is found that they were accepted into the
programme of their choice.
(b) Find the probability that the applicant applied for the Arts programme.
Two different applicants are chosen at random from the original group.
(c) Find the probability that both applicants applied to the Arts programme.
▶️Answer/Explanation
Ans:
(a) \((\frac{17+25}{13}=) \frac{42}{130}(\frac{21}{65}, 0.323076…)\)
(b) \((\frac{17}{17+25}=)\frac{17}{42} (0.404761…)\)
(c) \(\frac{41}{130} \times \frac{40}{129}\)
\(=\frac{1640}{16770} \approx 0.0978 (0.0977936…, \frac{164}{1677})\)
Question
]The ticket prices for a concert are shown in the following table.
| Ticket Type | Price (in Australian dollar, $) |
| Adult | 15 |
| Child | 10 |
| Student | 12 |
- A total of 600 tickets were sold.
- The total amount of money from ticket sales was $7816.
- There were twice as many adult tickets sold as child tickets
Let the number of adult tickets sold be x , the number of child tickets sold be y , and the
number of student tickets sold be z.
(a) Write down three equations that express the information given above.
(b) Find the number of each type of ticket sold.
▶️Answer/Explanation
Ans:
(a) x + y + z = 600
15x + 10y + 12z = 7816
x = 2y
(b) x = 308, y = 154, z = 138
