Question
The discrete random variable X has probability distribution
P(X = x) = pqx , x∈N, 0 < p < 1, q = 1 – p.
(i) Show that the probability generating function of X is given by
- Gx(t) = \(\frac{p}{1-qt}\)
- (ii) Hence find Var(X ) in terms of p . Express your answer in its simplest form. [9]
- b The random variable Y is defined by
Y = X1+ X2+ X3+ X4
where X1 , X2 , X3 , X4 is a random sample from the distribution of X .
Write down the probability generating function of Y .
Hence determine an expression for P(Y = 3) in terms of p . [4]
▶️Answer/Explanation
Ans:
(a)
(i)
GX (t) = p + pqt+ pq2t2 …
this is an infinite geometric series with first term p and common ratio qt, so (provided |qt| < 1 )
GX (t) = \(\frac{p}{1-qt}\)
(ii)
G’X (t) = \(\frac{pq}{(1-qt)^2}\)
G”X (t) = \(\frac{2pq^2}{(1-qt)^{3}}\)
use of Var (X) = G’X (1) + G”X (1) – [G’X (1))]2
=\(Var (X) =\frac{pq}{(1-q)^2}+ \frac{2pq^{2}}{(1-q)^{3}}- \frac{p^{2}q^{2} }{(1-q)^{4}}\)
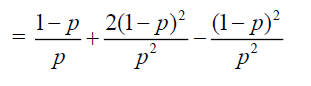
= \(\frac{1-p}{p^2}\)
(b)
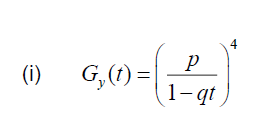
(ii)
METHOD 1
P( Y=3) = coefficient of t3 in the expansion of Gy (t)
=\(p^4\times \frac{4\times 5\times6}{3!}\times q^{3}\)
= 20p4 (1- p )3
METHOD 2
P (Y=3)= \(\frac{G_Y(0)}{3!}\)
G”Y (t)= \(\frac{120 p^{4}q^3}{(1-qt)^{7}}\)
P(Y= 3) = 20p4 (1 -p)3
Question
The discrete random variables \({X_n},{\text{ }}n \in {\mathbb{Z}^ + }\) have probability generating functions given by \({G_n}(t) = \frac{t}{n}\left( {\frac{{{t^n} – 1}}{{t – 1}}} \right)\).
Let \({X_{n – 1}}\) and \({X_{n + 1}}\) be independent.
a.Use the formula for the sum of a finite geometric series to show that
\[{\text{P}}({X_n} = k) = \left\{ {\begin{array}{*{20}{l}} {\frac{1}{n}}&{{\text{for }}1 \leqslant k \leqslant n} \\ 0&{{\text{otherwise}}} \end{array}.} \right.\][4]
b.Find \({\text{E}}({X_n})\).[3]
c.Find the set of values of \(n\) for which \({\text{E}}({X_{n – 1}} \times {X_{n + 1}}) < 2n\).[4]
▶️Answer/Explanation
Markscheme
using \(\left( {\frac{{{t^n} – 1}}{{t – 1}}} \right) = 1 + t + {t^2} + \ldots {t^{n – 1}}\) M1
\({G_n}(t) = 0 + \frac{t}{n} + \frac{{{t^2}}}{n} + \frac{{{t^3}}}{n} + \ldots \frac{{{t^n}}}{n} + 0 \times {t^{n + 1}} + 0 \times \ldots \) A1A1
Note: A1 for the non-zero terms, A1 for the observation that all other terms are zero.
the statement that the coefficient of \({t^k}\) gives \({\text{P}}({X_n} = k)\) R1
hence \({\text{P}}({X_n} = k) = \left\{ {\begin{array}{*{20}{l}} {\frac{1}{n}}&{{\text{for }}1 \leqslant k \leqslant n} \\ 0&{{\text{otherwise}}} \end{array}} \right.\) AG
[4 marks]
\({\text{E}}({X_n}) = 0 \times 0 + 1 \times \frac{1}{n} + 2 \times \frac{1}{n} + 3 \times \frac{1}{n} + \ldots n \times \frac{1}{n} + (n + 1) \times 0 + \ldots \times 0\) (M1)(A1)
\( = \frac{1}{n} \times \sum\limits_{k = 1}^{k = n} k \)
\( = \frac{1}{n} \times \frac{1}{2}n(n + 1) = \frac{{n + 1}}{2}\) A1
Note: Accept use of \(G'(1)\).
[3 marks]
\({X_{n – 1}}\) and \({X_{n + 1}}\) are independent \( \Rightarrow {\text{E}}({X_{n – 1}} \times {X_{n + 1}}) = {\text{E}}({X_{n – 1}}) \times {\text{E}}({X_{n + 1}})\) M1
\( = \frac{n}{2} \times \frac{{n + 2}}{2}\) A1
required to solve \({n^2} < 6n{\text{ }}({\text{or }}n + 2 < 8)\) M1
solution: \((2 \leqslant ){\text{ }}n < 6\) A1
[4 marks]
Question
The following table shows the probability distribution of the discrete random variable \(X\).

(a) Show that the probability generating function of \(X\) is given by
\[G(t) = \frac{{t{{(1 + t)}^2}}}{4}.\]
(b) Given that \(Y = {X_1} + {X_2} + {X_3} + {X_4}\), where \({X_1},{\text{ }}{X_2},{\text{ }}{X_3},{\text{ }}{X_4}\) is a random sample from the distribution of \(X\),
(i) state the probability generating function of \(Y\);
(ii) hence find the value of \({\text{P}}(Y = 8)\).
▶️Answer/Explanation
Markscheme
(a) \(G(t) = \frac{1}{4}t + \frac{1}{2}{t^2} + \frac{1}{4}{t^3}\) M1A1
\( = \frac{{t{{(1 + t)}^2}}}{4}\) AG
[2 marks]
(b) (i) \({\text{PGF of }} Y = {\left( {G(t)} \right)^4}\left( { = {{\left( {\frac{{t{{(1 + t)}^2}}}{4}} \right)}^4}} \right)\) A1
(ii) \({\text{P}}(Y = 8) = {\text{coefficient of }}{t^8}\) (M1)
\( = \frac{{^8{{\text{C}}_4}}}{{256}}\) (A1)
\( = \frac{{35}}{{128}} (0.273)\) A1
Note: Accept \(0.27\) or answers that round to \(0.273\).
[4 marks]
[MAI 4.9] DISCRETE DISTRIBUTIONS-neha
Question
The probability distribution of the discrete random variable \(X\) is given by the table

Find
(a) the expected value \(E(X)\) of \(X\).
(b) the mode of \(X\).
(c) the median of \(X\).
(d) the lower quartile \(Q_{1}\) and the upper quartile \(Q_{3}\).
▶️Answer/Explanation
Ans
(a) \(2.35\) (b) mode = \(1\) (c) median = \(2\) (d) \(Q_{1} = 1 \ Q_{3} = 3.5\)
Question
The probability distribution of the discrete random variable \(X\) is given by the table

Find the values of \(a\) and \(b\) given that \(E(X)\) = \(2.2\)
▶️Answer/Explanation
Ans
\(a = 0.2\) \(b = 0.4\)
