Question
Karl has three brown socks and four black socks in his drawer. He takes two socks at random
from the drawer.
(a) Complete the tree diagram.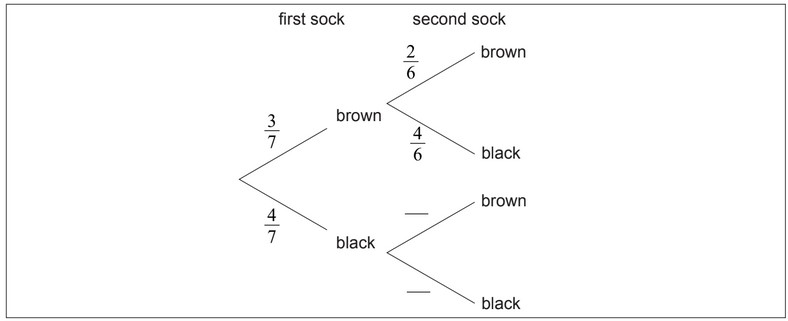
(b) Find the probability that Karl takes two socks of the same colour.
(c) Given that Karl has two socks of the same colour find the probability that he has two
brown socks.
Answer/Explanation
Ans:
(a)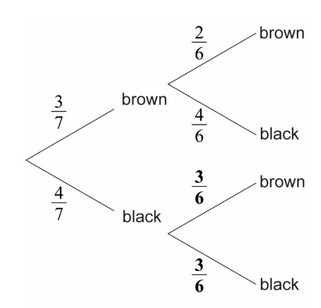 
(b) multiplying along branches and then adding outcomes
\(\frac{3}{7} \times \frac{2}{6} + \frac{4}{7} \times \frac{3}{6}\)
\(=\frac{18}{42}(=\frac{3}{7} \approx 0.429 (42.9%))\)
(c) use of conditional probability formula
\(\frac{(\frac{3}{7} \times \frac{2}{6})}{(\frac{3}{7})}\)
\(=\frac{6}{18}(=\frac{1}{3})(\frac{252}{756},0.333, 33.3%)\)
Question
The heights of apple trees in an orchard are normally distributed with a mean of \({\text{3.42 m}}\) and a standard deviation of \({\text{0.21 m}}\).
Write down the probability that a randomly chosen tree has a height greater than \({\text{3.42 m}}\).[1]
Write down the probability that a randomly chosen tree will be within 2 standard deviations of the mean of \({\text{3.42 m}}\).[1]
Use your graphic display calculator to calculate the probability that a randomly chosen tree will have a height greater than \({\text{3.35 m}}\).[2]
The probability that a particular tree is less than \(x\) metres high is \(0.65\). Find the value of \(x\).[2]
Answer/Explanation
Markscheme
\(0.5{\text{ }}\left( {50\% ,{\text{ }}\frac{{50}}{{100}},{\text{ }}\frac{1}{2}} \right)\) (A1) (C1)[1 mark]
\(0.954 (0.954499…, 95.4\%, 95.4499…\%)\) (A1) (C1)
Note: Accept \(95\%\) or \(0.95\).[1 mark]
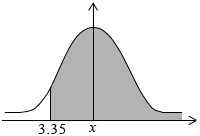(M1)
Note: Accept alternative methods.
\(0.631 (0.630558…, 63.1\%, 63.0558…\%)\) (A1) (C2)[2 marks]
(M1)
Note: Accept alternative methods.
\(3.50{\text{ }} (3.50091…)\) (A1) (C2)[2 marks]
Question
The daily January temperature of Cairns is normally distributed with a mean of 34°C and a standard deviation of 3.
Calculate the probability that the temperature on a randomly chosen day in January is less than 39°C.[2]
Calculate the expected number of days in January that the temperature will be more than 39°C.[2]
On a randomly chosen day in January, the probability that the temperature is above \(T\) °C is 0.7.
Find the value of \(T\).[2]
Answer/Explanation
Markscheme
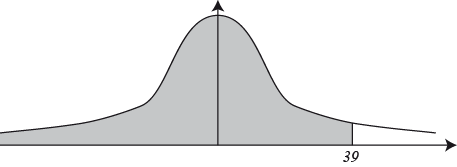(M1)
Note: Award (M1) for correctly shaded area.
\(0.952{\text{ }}(95.2\% ,{\text{ }}0.952209 \ldots )\) (A1) (C2)
\(31 \times (1 – 0.952209)\) (M1)
Note: Award (M1) for multiplying \(31\) by \(\left( {1 – {\text{ their answer to part (a)}}} \right)\).
\( = 1.48{\text{ }}(1.48150 \ldots )\) (A1)(ft) (C2)
Note: Follow through from part (a).
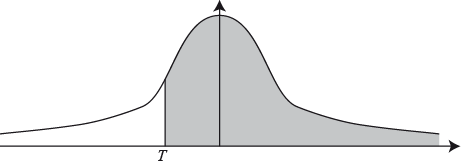(M1)
Note: Award (M1) for correctly shaded area.
\(32.4{\text{ }}(32.4267 \ldots )\) (A1) (C2)
Question
The weight, \(W\), of bags of rice follows a normal distribution with mean 1000 g and standard deviation 4 g.
Find the probability that a bag of rice chosen at random weighs between 990 g and 1004 g.[2]
95% of the bags of rice weigh less than \(k\) grams.
Find the value of \(k\).[2]
For a bag of rice chosen at random, \({\text{P}}(1000 – a < W < 1000 + a) = 0.9\).
Find the value of \(a\).[2]
Answer/Explanation
Markscheme
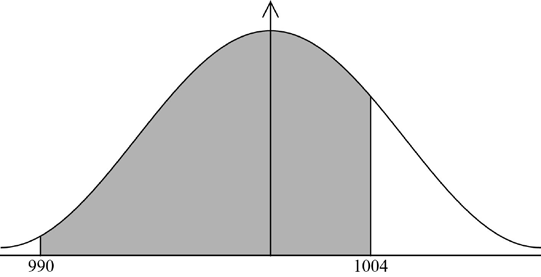(M1)
Note: Award (M1) for approximate curve with 990 and 1004 in correct place.
\(0.835\;\;\;(0.835135 \ldots ,{\text{ }}83.5\% )\) (A1) (C2)
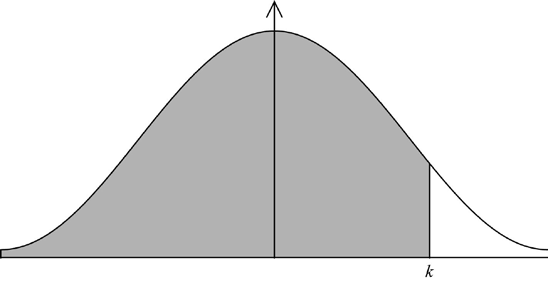(M1)
Note: Award (M1) for approximate curve with \(k\) placed to the right of the mean.
\(1010\;\;\;(1006.57 \ldots )\) (A1) (C2)
Note: Award full marks only for \(1010\), \(1007\) or an answer with more than \(4\) sf resulting from correct rounding of \(1006.57…\).
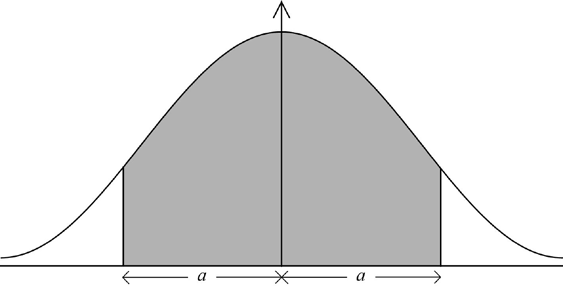(M1)
Note: Award (M1) for some indication of symmetry on diagram.
OR
\({\text{P}}(W < 1000 – a) = 0.05\;\;\;\)OR\(\;\;\;{\text{P}}(W > 1000 + a) = 0.05\) (M1)
Note: Award (M1) for probability with single inequality resulting from symmetry of diagram.
\((a = ){\text{ }}6.58\;\;\;(6.57941 \ldots )\) (A1) (C2)
Question
A factory makes metal bars. Their lengths are assumed to be normally distributed with a mean of 180 cm and a standard deviation of 5 cm.
On the following diagram, shade the region representing the probability that a metal bar, chosen at random, will have a length less than 175 cm.
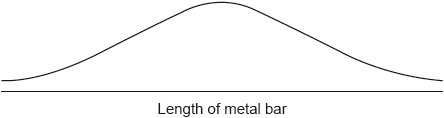[2]
A metal bar is chosen at random.
(i) The probability that the length of the metal bar is less than 175 cm is equal to the probability that the length is greater than \(h\) cm. Write down the value of \(h\).
(ii) Find the probability that the length of the metal bar is greater than one standard deviation above the mean.[4]
Answer/Explanation
Markscheme
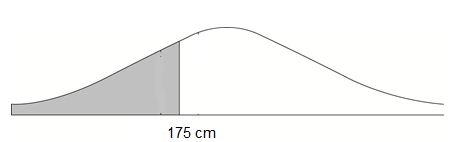(A1)(M1) (C2)
Notes: Award (A1) for the vertical line labelled as \(175{\text{ (cm)}}\).
Award (M1) for a vertical line drawn to the left of the mean with the area to the left of this line shaded.
Accept \(( – )1\) sd marked on the diagram for \(175\) (provided line is to the left of the mean).
(i) \(185{\text{ (cm)}}\) (A1)(C1)
(ii) \({\text{P(length}} > 185)\) (A1)(M1)
Note: Award (A1) for the vertical line labelled as \(185{\text{ (cm)}}\).
Award (M1) for a vertical line drawn to the right of the mean with the area to the right of this line shaded.
Accept 1 sd marked on the diagram for \(185\) (provided line is to the right of the mean).
\( = 0.159\;\;\;(0.158655 \ldots )\) (A1) (C3)