IB Mathematics SL 5.3 The derivative of functions AI HL Paper 2- Exam Style Questions- New Syllabus

Question

A particular park consists of a rectangular garden, of area \( A \) m², and a concrete path surrounding it. The park has a total area of 1200 m². The width of the path at the north and south side of the park is 2 m. The width of the path at the west and east side of the park is 1.5 m. The length of the park (along the north and south sides) is \( x \) metres, 3 \( < x < 300 \).

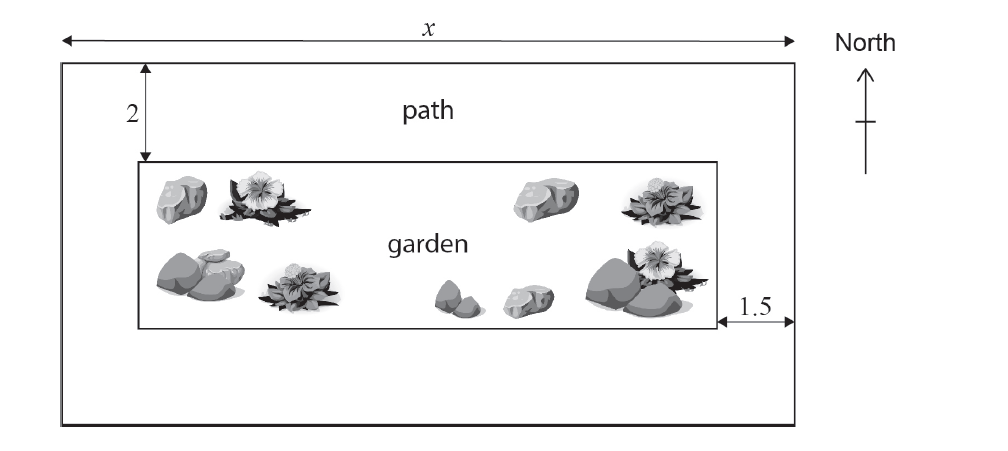
(a) Show that \( A = 1212 – 4x – 3600/x \).

(b) Find the possible dimensions of the park if the area of the garden is 800 m².

(c) Find an expression for \( dA/dx \).

(d) Use your answer from part (c) to find the value of \( x \) that will maximize the area of the garden.

(e) Find the maximum possible area of the garden.

▶️ Answer/Explanation

Markscheme

(a)
Method 1 (finding dimensions of garden):

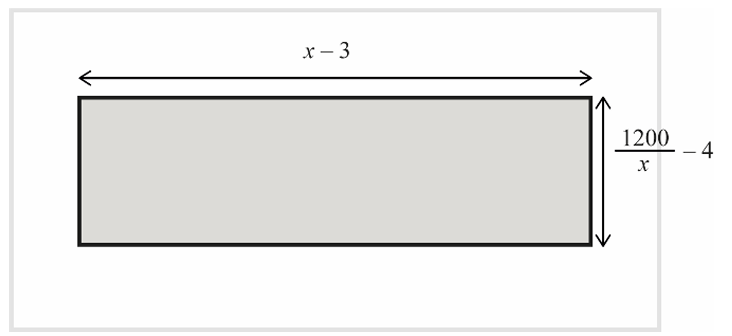
    Width of park = \( \frac{1200}{x} \) (A1)
    Length of garden = \( x – 3 \), width of garden = \( \frac{1200}{x} – 4 \) (A1)(A1)
    \( A = (x – 3) \times \left(\frac{1200}{x} – 4\right) \)
    \( = (x \times \frac{1200}{x}) – (x \times 4) – (3 \times \frac{1200}{x}) + (3 \times 4) \)
    \( = 1200 – 4x – \frac{3600}{x} + 12 \)
    \( = 1212 – 4x – \frac{3600}{x} \) (A1)(AG)
    Method 2 (subtracting the area of the path):

    Width of park = \( \frac{1200}{x} \) (A1)
    \( A = 1200 – 2x – 2x – 1.5 \left(\frac{1200}{x} – 4\right) – 1.5 \left(\frac{1200}{x} – 4\right) \)
    \( = 1200 – 4x – \frac{1800}{x} – \frac{1800}{x} \)
    \( = 1212 – 4x – \frac{3600}{x} \) (AG)
Result:
\( A = 1212 – 4x – \frac{3600}{x} \)

(b)
    \( 1212 – 4x – \frac{3600}{x} = 800 \) (M1)
    \( 4x + \frac{3600}{x} = 412 \)
    \( 4x^2 + 3600 = 412x \) (multiply by \( x \))
    \( 4x^2 – 412x + 3600 = 0 \)
    \( x^2 – 103x + 900 = 0 \) (divide by 4)
    \( x = \frac{103 \pm \sqrt{103^2 – 4 \times 1 \times 900}}{2} \)
    \( = \frac{103 \pm \sqrt{10609 – 3600}}{2} \)
    \( = \frac{103 \pm \sqrt{7009}}{2} \)
    \( \sqrt{7009} \approx 83.719 \)
    \( x \approx \frac{103 + 83.719}{2} \approx 93.3598 \) or \( x \approx \frac{103 – 83.719}{2} \approx 9.64011 \)
    Rounded: \( x = 93.4 \) m or \( x = 9.64 \) m
    Width = \( \frac{1200}{x} \)
    For \( x = 9.64 \): width = \( \frac{1200}{9.64} \approx 124.48 \) m ≈ 124 m
    For \( x = 93.4 \): width = \( \frac{1200}{93.4} \approx 12.853 \) m ≈ 12.9 m
Result:
\( x = 9.64 \) m, width = 124 m; \( x = 93.4 \) m, width = 12.9 m

(c)
    \( A = 1212 – 4x – \frac{3600}{x} \)
    \( \frac{dA}{dx} = 0 – 4 + \frac{d}{dx} \left(-\frac{3600}{x}\right) \)
    \( = -4 + 3600 \times \frac{1}{x^2} \) (using power rule)
    \( = -4 + \frac{3600}{x^2} \) (A1A1A1)
Result:
\( \frac{dA}{dx} = -4 + \frac{3600}{x^2} \)

(d)
    \( \frac{dA}{dx} = 0 \) (M1)
    \( -4 + \frac{3600}{x^2} = 0 \)
    \( \frac{3600}{x^2} = 4 \)
    \( x^2 = \frac{3600}{4} \)
    \( x^2 = 900 \)
    \( x = \pm 30 \)
    Since \( 3 < x < 300 \), \( x = 30 \) m (A1)
Result:
\( x = 30 \) m

(e)
    Substitute \( x = 30 \) into \( A \) (M1)
    \( A = 1212 – 4 \times 30 – \frac{3600}{30} \)
    \( = 1212 – 120 – 120 \)
    \( = 972 \) m² (A1)
Result:
972 m²

IB Mathematics SL 5.3 The derivative of functions AI HL Paper 2- Exam Style Questions- New Syllabus

Resources

Members

Company