Question 3. [Maximum mark: 15]
A hollow chocolate box is manufactured in the form of a right prism with a regular hexagonal base. The height of the prism is h cm, and the top and base of the prism have sides of length x cm.
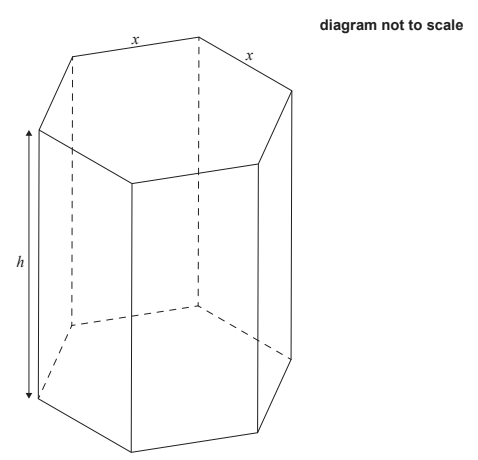
a. Given that \(sin 60\frac{\sqrt{3}}{2}\) show that the area of the base of the box is equal to \(\frac{3\sqrt{3x^{2}}}{2}\) [2]
b. Given that the total external surface area of the box is 1200 cm2, show that the volume of the box may be expressed as V = 300 \(\sqrt{3x}-\frac{9}{4}x^{3}\) [5]
c. Sketch the graph of V = 300 \(\sqrt{3x}-\frac{9}{4}x^{3}\) for 0 ≤ x ≤ 16. [2]
d. Find an expression for \(\frac{dV}{dx}\) . [2]
e. Find the value of x which maximizes the volume of the box. [2]
f. Hence, or otherwise, find the maximum possible volume of the box. [2]
Answer/Explanation
(a) splitting diagram into equilateral triangles area \(= 6(\frac{1}{2}x^{2}sin60)\)
\(=\frac{3\sqrt{3}x^{2}}{2}\)
(b) total surface area of prism
\(1200= 2 (3x^{2}\frac{\sqrt{3}}{2})+6xh\)
\(h= \frac{400-\sqrt{3x^{2}}}{2x}\)
\(volume of prism =\frac{3\sqrt{3}}{2}x^{2}h\)
\(= \frac{3\sqrt{3}}{2}x^{2}(\frac{400-\sqrt{3x^{2}}}{2x})
\(= 300\sqrt{3x}-\frac{9}{4}x^{3}\)
(c) 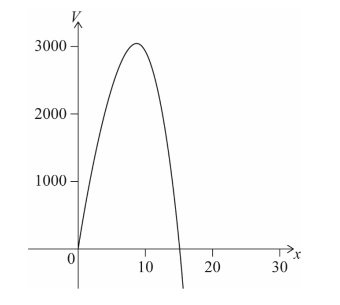
(d)\(\frac{dV}{dx}= 300\sqrt{3}-\frac{27}{4}x^{2}\)
(e) from the graph of V or\(\frac{dV}{dx}OR solving \frac{dV}{dx}= 0\) \( x = 8.77 (8.77382…)\)
(f) from the graph of V OR substituting their value for x into V
\(V_{max}= 3040 cm^{2}\rightarrow (3039.34…)\)
Question 2. [Maximum mark: 16]
The cross-sectional view of a tunnel is shown on the axes below. The line [AB] represents a vertical wall located at the left side of the tunnel.
The height, in metres, of the tunnel above the horizontal ground is modelled by y = -0.1x 3 + 0.8x 2 , 2 ≤ x ≤ 8, , relative to an origin O.
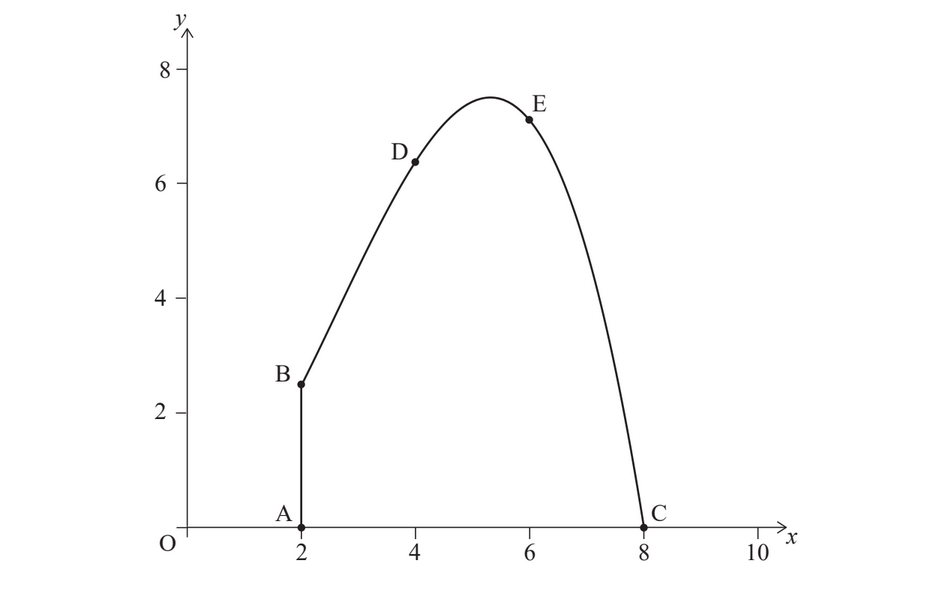
Point A has coordinates (2 , 0), point B has coordinates (2 , 2.4), and point C has coordinates (8 , 0).
a. (i) Find \(\frac{dy}{dx}\)
(ii) Hence find the maximum height of the tunnel. [6]
b. Find the height of the tunnel when
(i) x = 4 .
(ii)x = 6 . [3]
c. Use the trapezoidal rule, with three intervals, to estimate the cross-sectional area of the tunnel. [3]
d. (i) Write down the integral which can be used to find the cross-sectional area of the tunnel.
(ii) Hence find the cross-sectional area of the tunnel. [4]
Answer/Explanation
(a) (i) \(\frac{dy}{dx}\)= \(-0.3x^{2}\)+ 1.6x
(ii) \(-0.3x^{2}\)+ 1.6x = 0 x = 5.33 (5.3333… \(\frac{16}{3 })\) \(y = -0.1 5.3333…. + 0.8 5.3333….7.59 m (7.58519…)\)
(b) (i) 6.4 m(ii) 7.2 m
(c) \(A = \frac{1}{2}\times 2((2.4+0)+2(6.4+7.2))\)= 29 m2
(d)(i) \(A = \int ^{8}_{2}-0.1x^{3}+ 0.8x^{2}dx\) OR
\(A = \int ^{8}_{2}\)ydx
(ii) \(A = 32.4 m^{2}\)
Question
A cafe makes x litres of coffee each morning. The cafe’s profit each morning, C, measured
in dollars, is modelled by the following equation
\(C=\frac{x}{10}\left ( k^{2}-\frac{3}{100}x^{2} \right )\)
where k is a positive constant.
(a) Find an expression for \(\frac{dC}{dx}\) in terms of k and x . [3]
(b) Hence find the maximum value of C in terms of k . Give your answer in the form pk3,
where p is a constant. [4]
The cafe’s manager knows that the cafe makes a profit of $426 when 20 litres of coffee are
made in a morning.
(c) (i) Find the value of k .
(ii) Use the model to find how much coffee the cafe should make each morning to
maximize its profit. [3]
(d) Sketch the graph of C against x , labelling the maximum point and the x-intercepts
with their coordinates. [3]
The manager of the cafe wishes to serve as many customers as possible.
(e) Determine the maximum amount of coffee the cafe can make that will not result in a
loss of money for the morning. [2]
Answer/Explanation
Ans
2. (a) attempt to expand given expression OR attempt at product rule (M1)
\(C=\frac{xk^{2}}{10}-\frac{3x^{3}}{1000})
\(\frac{dC}{dx}=\frac{k^{2}}{10}-\frac{9x^{2}}{1000}\)
Note: Award M1 for power rule correctly applied to at least one term
and A1 for correct answer.
[3 marks]
(b) equating their \(\frac{dC}{dx}\) to zero (M1)
\(\frac{k^{2}}{10}-\frac{9x^{2}}{1000}=0\)
\(x^{2}=\frac{100k^{2}}{9}\)
\(x=\frac{10k}{3}\) (A1)
substituting their x back into given expression (M1)
\(C_{max}=\frac{10k}{30}\left ( k^{2}-\frac{300k^{2}}{900} \right )\)
\(C_{max}=\frac{2k}{9}\left ( 0.222…k^{3} \right )\) A1
[4 marks]
(c) (i) substituting 20 into given expression and equating to 426 M1
\(426=\frac{20}{10}\left ( k^{2}-\frac{3}{100}(20)^{2} \right )\)
k =15 A1
(ii) 50 A1
[3 marks]
continued
(d) 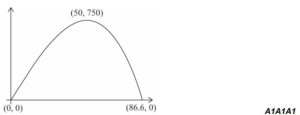
Note: Award A1 for graph indicating an increasing and then decreasing function (drawn in first
quadrant), A1 for maximum labelled and A1 for graph drawn for positive x, passing
through the origin and 86.6 which is marked on the x-axis or its coordinates are given.
[3 marks]
(e) setting their expression for C to zero OR choosing correct x-intercept on
their graph of C (M1)
xmax = 86.6 (86.6025 ) … litres A1
[2 marks]
Total [15 marks]
Question
A student investigating the relationship between chemical reactions and temperature finds
the Arrhenius equation on the internet.
\(k=Ae^{-\frac{c}{T}}\)
This equation links a variable k with the temperature T, where A and c are positive
constants and T > 0.
(a) Show that \(\frac{dk}{dT}\) is always positive. [3]
(b) Given that \(\lim_{T\rightarrow \infty }k=A \ and \ \lim_{T\rightarrow 0}k=0\), sketch the graph of k against T. [3]
The Arrhenius equation predicts that the graph of ln k against \(\frac{1}{T}\) is a straight line.
(c) Write down
(i) the gradient of this line in terms of c ;
(ii) the y-intercept of this line in terms of A. [4]
The following data are found for a particular reaction, where T is measured in Kelvin
and k is measured in cm3 mol−1 s−1:
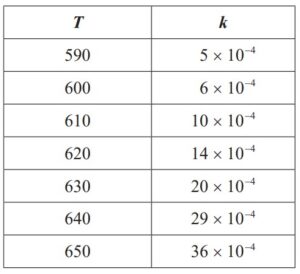
(d) Find the equation of the regression line for ln k on \(\frac{1}{T}\) [2]
(e) Find an estimate of
(i) c ;
(ii) A.
It is not required to state units for these values. [3]
▶️Answer/Explanation
Ans
4. (a) attempt to use chain rule, including the differentiation of \(\frac{1}{T}\) (M1)
\(\frac{dk}{dT}=A\times \frac{c}{T^{2}}\times e^{-\frac{c}{T}}\)
this is the product of positive quantities so must be positive R1
Note: The R1 may be awarded for correct argument from their derivative.
R1 is not possible if their derivative is not always positive.
[3 marks]
(b)
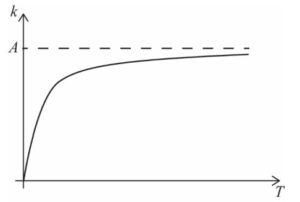
A1A1A1
Note: Award A1 for an increasing graph, entirely in first quadrant, becoming
concave down for larger values of T, A1 for tending towards the origin
and A1 for asymptote labelled at k = A .
[3 marks]
(c) taking ln of both sides OR substituting y = ln x and \(x=\frac{1}{T}\) (M1)
\(ln k=ln A=-\frac{c}{T}\ OR \ y=-cx+ln A\) (A1)
(i) so gradient is −c A1
(ii) y-intercept is ln A A1
Note: The implied (M1) and (A1) can only be awarded if both correct answers are
seen. Award zero if only one value is correct and no working is seen.
[4 marks]
continued…
(d) an attempt to convert data to \(\frac{1}{T}\) ln k (M1)
e.g. at least one correct row in the following table
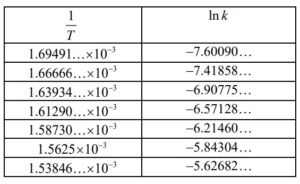
line is \(ln k=-13400\times \frac{1}{T}+15.0 \left ( =-13383.1…\times \frac{1}{T}+15.0107 \right )\) A1
[2 marks]
(e) (i) c =13400 (13383.1 ) … A1
(ii) attempt to rearrange or solve graphically ln 15.0107 A = … (M1)
A = (3300000 3304 258…) A1
Note: Accept an A value of 3269017… from use of 3sf value.
[3 marks]
Total [15 marks]
