Question
The strength of earthquakes is measured on the Richter magnitude scale, with values
typically between 0 and 8 where 8 is the most severe.
The Gutenberg–Richter equation gives the average number of earthquakes per year, N,
which have a magnitude of at least M. For a particular region the equation is
\(log_{10}N=a-M\), for some \(a\epsilon \mathbb{R}\).
This region has an average of 100 earthquakes per year with a magnitude of at least 3.
(a) Find the value of a.
The equation for this region can also be written as \(N=\frac{b}{M^M}\).
(b) Find the value of b.
(c) Given 0<M<8, find the range for N.
The expected length of time, in years, between earthquakes with a magnitude of at least M is \(\frac{1}{N}\).
Within this region the most severe earthquake recorded had a magnitude of 7.2.
(d) Find the expected length of time between this earthquake and the next earthquake of at least this magnitude. Give your answer to the nearest year.
▶️Answer/Explanation
Ans:
(a) \(log_{10} 100 = a – 3\)
a = 5
(b) EITHER
\(N = 10^{5-M}\)
OR
\(100=\frac{b}{10^3}\)
THEN
b = 100000\((=10^5)\)
(c) 0.001<N<100000 \((10^{-3}<N<10^5)\)
(d) \(N=\frac{10^5}{10^{7.2}}(=0.0063095…)\)
length of time = \(\frac{1}{0.0063095…}=10^{2.2}\)
= 158 years
Question
The function f is defined by \(f(x) = \frac{2}{x} + 3x^2 – 3, x \neq 0\).
(a) Find f'(x)
(b) Find the equation of the normal to the curve y = f(x) at (1, 2) in the form ax + by + d = 0, where \(a, b, d\epsilon \mathbb{Z}\).
▶️Answer/Explanation
Ans:
(a) \(f'(x) = -2x^{-2}+6x\) OR \(f'(x) = -\frac{2}{x^2}+6x\)
(b) finding gradient at x = 1
\(\left.\begin{matrix}
\frac{dy}{dx}
\end{matrix}\right|_{x=1}=4\)
finding the perpendicular gradient
\(m_{\perp} = -\frac{1}{4}\)
\(2=-\frac{1}{4}(1)+c\) OR \(y-2 = -\frac{1}{4}(x-1)\)
x + 4y – 9 = 0
Question
The wind chill index W is a measure of the temperature, in \(^∘C\), felt when taking into account the effect of the wind.
When Frieda arrives at the top of a hill, the relationship between the wind chill index and the speed of the wind v in kilometres per hour \((km h^{-1}\)) is given by equation
\(W = 19.34 – 7.405 v^{0.16}\)
(a) Find an expression for \(\frac{dW}{dv}\).
When Frieda arrives at the top of a hill, the speed of the wind is 10 kilometres per hour and increasing at a rate of \(5kmh^{-1} minute^{-1}\).
(b) Find the rate of change of W at this time.
▶️Answer/Explanation
Ans:
(a) use of power rule
\(\frac{dW}{dv} = -1848v^{-0.84}\) OR \(-1.18v^{-0.84}\)
(b) \(\frac{dv}{dt}=5\)
\(\frac{dW}{dt}=\frac{dv}{dt} \times \frac{dW}{dv}\)
\((\frac{dW}{dt}=-5 \times 1.1848v^{-0.84}\))
when v = 10
\(\frac{dW}{dt} = -5 \times 1.1848 \times 10^{-0.84}\)
– 0.856 (-0.856278…) \(^oC min^{-1}\)
Question
1. The height of a baseball after it is hit by a bat is modelled by the function
\(h(t)=-4.8t^2 + 21t + 1.2\)
where h(t) is the height in metres above the ground and t is the time in seconds after the ball was hit.
(a) Write down the height of the ball above the ground at the instant it is hit by the bat.
(b) Find the value of t when the ball hits the ground.
(c) State an appropriate domain for t in this model.
▶️Answer/Explanation
Ans:
(a) 1.2 metres
(b) \(-4.8 t^2 + 21t + 1.2 = 0\)
(t=) 4.43 s (4.431415…s)
(c) \(0 \leq t \leq 4.43\) OR [0, 4.43]
Question
The figure below shows the graphs of functions \(f_1 (x) = x\) and \(f_2 (x) = 5 – x^2\).
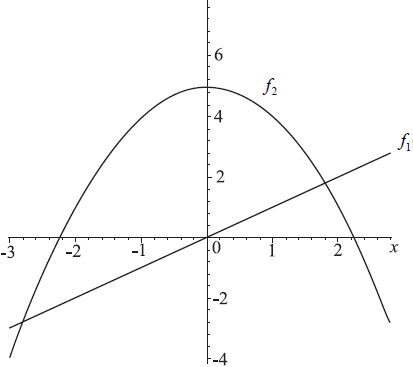
a.(i) Differentiate \(f_1 (x) \) with respect to x.
(ii) Differentiate \(f_2 (x) \) with respect to x.[3]
b.Calculate the value of x for which the gradient of the two graphs is the same.[2]
c.Draw the tangent to the curved graph for this value of x on the figure, showing clearly the property in part (b).[1]
▶️Answer/Explanation
Markscheme
(i) \(f_1 ‘ (x) = 1\) (A1)
(ii) \(f_2 ‘ (x) = – 2x\) (A1)(A1)
(A1) for correct differentiation of each term. (C3)[3 marks]
\(1 = – 2x\) (M1)
\(x = – \frac{1}{2}\) (A1)(ft) (C2)[2 marks]
(A1) is for the tangent drawn at \(x = \frac{1}{2}\) and reasonably parallel to the line \(f_1\) as shown.
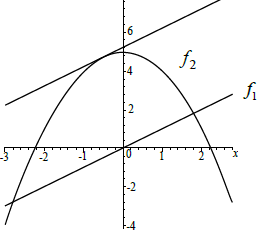(A1) (C1)[1 mark]