IIT JEE Main Maths -Unit 10- Standard form and general equation of a circle- Study Notes-New Syllabus
IIT JEE Main Maths -Unit 10- Standard form and general equation of a circle – Study Notes – New syllabus
IIT JEE Main Maths -Unit 10- Standard form and general equation of a circle – Study Notes -IIT JEE Main Maths – per latest Syllabus.
Key Concepts:
- Circle: Standard Form and General Equation
- Circle Passing Through Three Points
Circle: Standard Form and General Equation
A circle is the locus of all points whose distance from a fixed point (called center) is constant (called radius).
1. Standard Form of the Equation of a Circle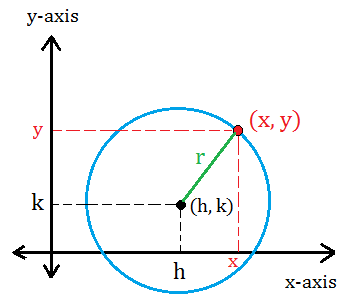
If the circle has center \( (h, k) \) and radius \( r \), then its equation is:
\( (x – h)^2 + (y – k)^2 = r^2 \)
- This is the most important form in JEE.
- The distance between any point \( (x, y) \) on the circle and center \( (h, k) \) equals \( r \).
2. General Equation of a Circle
The general form is a quadratic equation in \( x \) and \( y \):
\( x^2 + y^2 + 2gx + 2fy + c = 0 \)
This represents a circle provided: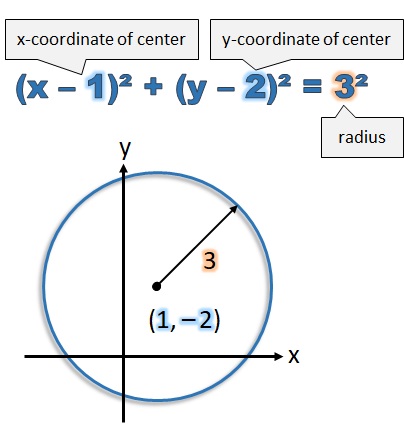
\( g^2 + f^2 – c > 0 \)
Center and Radius:
Center \( = (-g, -f) \)
Radius \( = \sqrt{g^2 + f^2 – c} \)
3. Converting Between Forms
(a) From general form to standard form
Complete the squares:
\( x^2 + y^2 + 2gx + 2fy + c = 0 \)
Rewrite:
\( (x + g)^2 – g^2 + (y + f)^2 – f^2 + c = 0 \)
Thus:
\( (x + g)^2 + (y + f)^2 = g^2 + f^2 – c \)
4. Special Cases
- Circle centered at origin: \( x^2 + y^2 = r^2 \)
- Circle touches origin: \( g^2 + f^2 = c \)
- Radius zero: Represents a point circle
- No real circle: If \( g^2 + f^2 – c < 0 \)
5. Condition for Circle to Touch an Axis
- Tangent to x-axis: center \( (h, k) \) with \( |k| = r \)
- Tangent to y-axis: center \( (h, k) \) with \( |h| = r \)
Example
Find the equation of a circle with center \( (3, -2) \) and radius \( 5 \).
▶️ Answer / Explanation
Using standard form:
\( (x – 3)^2 + (y + 2)^2 = 25 \)
Answer: \( (x – 3)^2 + (y + 2)^2 = 25 \)
Example
Convert the equation \( x^2 + y^2 – 6x + 4y – 12 = 0 \) to standard form and find its center and radius.
▶️ Answer / Explanation
Rewrite:
\( (x^2 – 6x) + (y^2 + 4y) = 12 \)
Complete square:
\( x^2 – 6x = (x – 3)^2 – 9 \)
\( y^2 + 4y = (y + 2)^2 – 4 \)
So:
\( (x – 3)^2 – 9 + (y + 2)^2 – 4 = 12 \)
\( (x – 3)^2 + (y + 2)^2 = 25 \)
Center = \( (3, -2) \)
Radius = 5
Example
The general equation of a circle is \( x^2 + y^2 + 4x – 6y + k = 0 \). For what value of \( k \) does the radius become 7?
▶️ Answer / Explanation
Compare with:
\( x^2 + y^2 + 2gx + 2fy + c = 0 \)
So \( g = 2,\ f = -3,\ c = k \)
Radius \( r = \sqrt{g^2 + f^2 – c} \)
Given \( r = 7 \)
\( 7^2 = g^2 + f^2 – c \)
\( 49 = 4 + 9 – k \)
\( 49 = 13 – k \Rightarrow k = 13 – 49 = -36 \)
Answer: \( k = -36 \)
Circle Passing Through Three Points
A unique circle can always be drawn through any three non-collinear points. Using these points, we can find the equation of the circle.
1. Standard Method (Most Used in JEE)
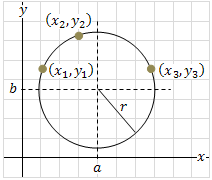
General equation of a circle:
\( x^2 + y^2 + 2gx + 2fy + c = 0 \)
Circle passes through three points \( P(x_1,y_1),\ Q(x_2,y_2),\ R(x_3,y_3) \), so:
\( x_1^2 + y_1^2 + 2gx_1 + 2fy_1 + c = 0 \)
\( x_2^2 + y_2^2 + 2gx_2 + 2fy_2 + c = 0 \)
\( x_3^2 + y_3^2 + 2gx_3 + 2fy_3 + c = 0 \)
Solving this system gives the values of \( g, f, c \), and hence the required circle.
2. Determinant Form (Fastest Method)
The circle through 3 points is:
\( \begin{vmatrix} x^2 + y^2 & x & y & 1 \\ x_1^2 + y_1^2 & x_1 & y_1 & 1 \\ x_2^2 + y_2^2 & x_2 & y_2 & 1 \\ x_3^2 + y_3^2 & x_3 & y_3 & 1 \end{vmatrix} = 0 \)
This is the most powerful formula used in JEE for quick solving.
3. Condition for Circle to Exist
The three points must be non-collinear.
Collinearity check:
\( \begin{vmatrix} x_1 & y_1 & 1 \\ x_2 & y_2 & 1 \\ x_3 & y_3 & 1 \end{vmatrix} \neq 0 \)
4. Special Shortcut for JEE
If the three points are:
- Points symmetric in some way
- Points on coordinate axes
- Right-angled triangle vertices
Then we can use geometry:
- If triangle is right-angled → circle is drawn with hypotenuse as diameter
- If center lies on axis → use special forms
Very helpful for MCQs.
Example
Find the equation of the circle passing through \( (1,0),\ (0,1),\ (-1,0) \).
▶️ Answer / Explanation
Observation: These are symmetric points on axes.
The circle will be centered at origin.
Find radius:
Distance from origin to \( (1,0) \) = 1
Equation:
\( x^2 + y^2 = 1 \)
Example
Find equation of circle through points \( (1,2),\ (3,4),\ (5,0) \).
▶️ Answer / Explanation
Let equation be:
\( x^2 + y^2 + 2gx + 2fy + c = 0 \)
Substitute points:
(1) \( 1 + 4 + 2g + 4f + c = 0 \) → \( 2g + 4f + c = -5 \)
(2) \( 9 + 16 + 6g + 8f + c = 0 \) → \( 6g + 8f + c = -25 \)
(3) \( 25 + 0 + 10g + 0 + c = 0 \) → \( 10g + c = -25 \)
Subtract (2) – (1):
\( 4g + 4f = -20 \Rightarrow g + f = -5 \)
Subtract (3) – (2):
\( 4g – 8f = 0 \Rightarrow g = 2f \)
Solve:
\( g = 2f,\quad g + f = -5 \Rightarrow 3f = -5 \Rightarrow f = -\dfrac{5}{3} \)
\( g = 2f = -\dfrac{10}{3} \)
Use equation (3):
\( 10\left(-\dfrac{10}{3}\right) + c = -25 \)
\( c = -25 + \dfrac{100}{3} = \dfrac{25}{3} \)
Final circle:
\( x^2 + y^2 – \dfrac{20}{3}x – \dfrac{10}{3}y + \dfrac{25}{3} = 0 \)
Example
Find equation of circle passing through \( (2,3),\ (4,5),\ (6,3) \).
▶️ Answer / Explanation
Use determinant form:
\( \begin{vmatrix} x^2 + y^2 & x & y & 1 \\ 13 & 2 & 3 & 1 \\ 41 & 4 & 5 & 1 \\ 45 & 6 & 3 & 1 \end{vmatrix} = 0 \)
Expanding (skipping intermediate algebra for speed):
Equation reduces to:
\( x^2 + y^2 – 8x – 4y + 20 = 0 \)
Answer: \( x^2 + y^2 – 8x – 4y + 20 = 0 \)
Notes and Study Materials
- Concepts of Circle
- Circle Master File
- Circle Revision Notes
- Circle Formulae
- Circle Reference Book
- Circle Past Many Years Questions and Answer
Examples and Exercise
IIT JEE (Main) Mathematics ,”Circle” Notes ,Test Papers, Sample Papers, Past Years Papers , NCERT , S. L. Loney and Hall & Knight Solutions and Help from Ex- IITian
About this unit
Standard form of equation of a circle, general form of the equation of a circle, its radius and centre, equation of a circle when the endpoints of a diameter are given, points of intersection of a line and a circle with the centre at the origin and condition for a line to be tangent to a circle, equation of the tangent.
IITian Academy Notes for IIT JEE (Main) Mathematics – Circle
The success mantra of the JEE is practice and hard work. Gone are the days when students used to spend hours in attempting one question. Now it is an era of multiple choice questions. The JEE Mathematics questions test a student’s acquired knowledge as well as his aptitude. We have excellent notes prepared by Ex-IITian to best match the requirement of the exam.Focus is given on problem solving skills and small tips and tricks to do it faster and easier. We , Ex-IITian at https://www.iitianacademy.com. will make sure you understand the concept well.
IIT JEE (Main) Mathematics, Circle Solved Examples and Practice Papers.
Get excellent practice papers and Solved examples to grasp the concept and check for speed and make you ready for big day. These Question Papers are prepared by Ex-IITIan for IIT JEE (Main) Mathematics , Circle.
S. L. Loney IIT JEE (Main) Mathematics
This book is the one of the most beautifully written book by the author. Trigonometry is considered to be one of the easiest topics in mathematics by the aspirants of IIT JEE, AIEEE and other state level engineering examination preparation. It would not be untrue to say that most of the sources have taken inspiration from this book as it is the most reliable source. The best part of this book is its coverage in Heights and Distances and Inverse Trigonometric Functions. The book gives a very good learning experience and the exercises which follow are not only comprehensive but they have both basic and standard questions.. I will help you online for any doubt / clarification.
Hall & Knight IIT JEE (Main) Mathematics
Algebra by Hall and Knight is one of the best books for JEE preparation. Students preparing for IIT JEE and other engineering entrance exams as well as students appearing for board exams should read this everyday, especially to master Algebra and Probability. Hall and Knight have explained the concepts logically in their book.
IIT JEE (Main) Mathematics Assignments
Chapter wise assignments are being given by teachers to students to make them understand the chapter concepts. Its extremely critical for all CBSE students to practice all assignments which will help them in gaining better marks in examinations. All assignments available for free download on the website are developed by the best teachers having many years of teaching experience in CBSE schools all over the country. Students, teachers and parents are advised to contact me online incase of any doubt / clarification.
Past Many Years (40 Years) Questions IIT JEE (Main) Mathematics Solutions Circle
Past 40 Years Question Papers Solutions for IIT JEE (Main) Mathematics Circle are provided here with simple step-by-step explanations. These solutions for Circle are extremely popular among IIT JEE (Main) students for Chemistry . Circle Solutions come handy for quickly completing your homework and preparing for exams. All questions and answers from the Past Many Years Question Papers Book of IIT JEE (Main) Mathematics Chapter Circle are provided here for . I will help you online for any doubt / clarification.
