IIT JEE Main Maths -Unit 4- Permutations (nPr)- Study Notes-New Syllabus
IIT JEE Main Maths -Unit 4- Permutations (nPr) – Study Notes – New syllabus
IIT JEE Main Maths -Unit 4- Permutations (nPr) – Study Notes -IIT JEE Main Maths – per latest Syllabus.
Key Concepts:
- Permutations — Definition, Formulae, and Special Cases
- Combinations — Definition, Formulae, and Properties (Including Selection with Restrictions)
Permutations — Definition, Formulae, and Special Cases
A permutation is an arrangement of some or all of a given number of distinct objects, taking into account the order of arrangement.

In simple words, permutation means the number of possible arrangements when order matters.
Formula for Number of Permutations
If \( n \) distinct objects are arranged taking \( r \) at a time, the number of permutations is given by:
$ P(n, r) = nP_r = \dfrac{n!}{(n – r)!}$
Where:
- \( n! = n \times (n – 1) \times (n – 2) \times \dots \times 1 \)
- \( n! = 1 \) if \( n = 0 \)
Important Cases
- When all objects are taken: \( P(n, n) = n! \)
- When no object is taken: \( P(n, 0) = 1 \)
Permutations of Distinguishable Objects
If there are \( n \) distinct objects in which:
- \( p_1 \) are alike of one kind,
- \( p_2 \) are alike of another kind, etc.
Then, the total number of permutations is:
$ \text{Total permutations} = \dfrac{n!}{p_1! \, p_2! \, p_3! \dots} $
Permutations with Repetition
If each of \( n \) distinct objects can be repeated \( r \) times, then the total number of permutations is:
$n^r$
Circular Permutations
When objects are arranged around a circle, rotations of the same arrangement are considered identical.
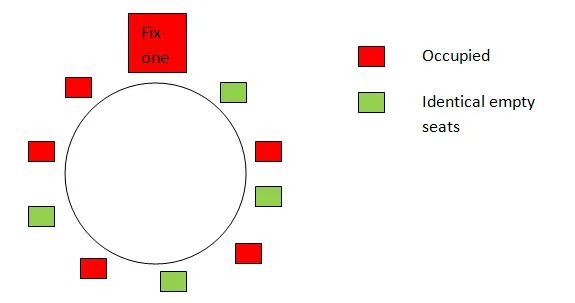
| Type | Formula | Remarks |
|---|---|---|
| Circular permutation of \( n \) distinct objects | \( (n – 1)! \) | Rotation considered same |
| Circular permutation (clockwise & anticlockwise same) | \( \dfrac{(n – 1)!}{2} \) | Used in necklace-type problems |
Special Results
- Number of ways to arrange \( n \) distinct objects = \( n! \)
- Arranging \( n \) objects in a line when some are identical = \( \dfrac{n!}{p_1!p_2! \dots} \)
- If the first or last position is fixed, reduce \( n \) by 1.
Example
How many 3-letter words can be formed using the letters of the word “DELTA” without repetition?
▶️ Answer / Explanation
Total letters = 5, we need to choose 3 and arrange them.
\( 5P_3 = \dfrac{5!}{(5 – 3)!} = \dfrac{120}{2} = 60 \)
Answer: 60 possible 3-letter words.
Example
How many different words can be formed with the letters of the word “BANANA”?
▶️ Answer / Explanation
Total letters = 6, with 3 A’s and 2 N’s identical.
Number of distinct arrangements:
\( \dfrac{6!}{3! \times 2!} = \dfrac{720}{12} = 60 \)
Answer: 60 distinct arrangements.
Example
In how many ways can 6 people sit around a circular table if two particular persons must always sit together?
▶️ Answer / Explanation
Step 1: Treat the two persons who must sit together as one block.
This reduces total persons to \( (6 – 1) = 5 \) effective people.
Step 2: Circular permutations = \( (5 – 1)! = 4! = 24 \)
Step 3: The two persons in the block can exchange seats among themselves = \( 2! = 2 \) ways.
Total arrangements: \( 24 \times 2 = 48 \)
Answer: 48 possible seating arrangements.
Notes and Study Materials
- Concepts of Permutations & Combinations
- Permutations & Combinations Master File
- Permutations & Combinations Revision Notes
- Permutations & Combinations Formulae
- Permutations & Combinations Reference Book
- Permutations & Combinations Past Many Years Questions and Answer
Examples and Exercise
IIT JEE (Main) Mathematics ,” Permutations & Combinations” Notes ,Test Papers, Sample Papers, Past Years Papers , NCERT , S. L. Loney and Hall & Knight Solutions and Help from Ex- IITian
About this unit
The fundamental principle of counting. Permutation as an arrangement and combination as selection . The meaning of P (n,r) and C (n,r). Simple applications.
IITian Academy Notes for IIT JEE (Main) Mathematics – Permutations & Combinations
The success mantra of the JEE is practice and hard work. Gone are the days when students used to spend hours in attempting one question. Now it is an era of multiple choice questions. The JEE Mathematics questions test a student’s acquired knowledge as well as his aptitude. We ahve execellent notes prepared by Ex-IITian to best match the requirement of the exam.Focus is given on problem solving skills and small tips and trciks to do it faster and easier. We , Ex-IITian at https://www.iitianacademy.com. will make sure you understand the concept well.
IIT JEE (Main) Mathematics, Permutations & Combinations Solved Examples and Practice Papers.
Get excellent practice papers and Solved examples to grasp the concept and check for speed and make you ready for big day. These Question Papers are prepared by Ex-IITIan for IIT JEE (Main) Mathematics , Permutations & Combinations.
S. L. Loney IIT JEE (Main) Mathematics
This book is the one of the most beautifully written book by the author. Trigonometry is considered to be one of the easiest topics in mathematics by the aspirants of IIT JEE, AIEEE and other state level engineering examination preparation. It would not be untrue to say that most of the sources have taken inspiration from this book as it is the most reliable source. The best part of this book is its coverage in Heights and Distances and Inverse Trigonometric Functions. The book gives a very good learning experience and the exercises which follow are not only comprehensive but they have both basic and standard questions.. I will help you online for any doubt / clarification.
Hall & Knight IIT JEE (Main) Mathematics
Algebra by Hall and Knight is one of the best books for JEE preparation. Students preparing for IIT JEE and other engineering entrance exams as well as students appearing for board exams should read this everyday, especially to master Algebra and Probability. Hall and Knight have explained the concepts logically in their book.
IIT JEE (Main) Mathematics Assignments
Chapter wise assignments are being given by teachers to students to make them understand the chapter concepts. Its extremely critical for all CBSE students to practice all assignments which will help them in gaining better marks in examinations. All assignments available for free download on the website are developed by the best teachers having many years of teaching experience in CBSE schools all over the country. Students, teachers and parents are advised to contact me online incase of any doubt / clarification.
Past Many Years (40 Years) Questions IIT JEE (Main) Mathematics Solutions Permutations & Combinations
Past 40 Years Question Papers Solutions for IIT JEE (Main) Mathematics Permutations & Combinations are provided here with simple step-by-step explanations. These solutions for Permutations & Combinations are extremely popular among IIT JEE (Main) students for Chemistry . Permutations & Combinations Solutions come handy for quickly completing your homework and preparing for exams. All questions and answers from the Past Many Years Question Papers Book of IIT JEE (Main) Mathematics Chapter Permutations & Combinations are provided here for . I will help you online for any doubt / clarification.
