IIT JEE Main Maths -Unit 11- Equation of a line and plane- Study Notes-New Syllabus
IIT JEE Main Maths -Unit 11- Equation of a line and plane – Study Notes – New syllabus
IIT JEE Main Maths -Unit 11- Equation of a line and plane – Study Notes -IIT JEE Main Maths – per latest Syllabus.
Key Concepts:
- Equation of a Line in 3D
- Equation of a Plane
- Equation of Line of Intersection of Two Planes
Equation of a Line in 3D
A line in 3D is uniquely determined by a point through which it passes and a direction in which it moves. This direction is represented using direction ratios or a direction vector. There are three standard forms of a line in 3D.
Vector Form of a Line
If a line passes through point \( A(x_1, y_1, z_1) \) and has direction ratios \( (a, b, c) \), then its vector equation is
\( \vec{r} = \vec{a} + \lambda\,(a\,\hat{i} + b\,\hat{j} + c\,\hat{k}) \)
- \( \lambda \) is a real parameter.
- \( \vec{a} = x_1\hat{i} + y_1\hat{j} + z_1\hat{k} \) is the position vector of point A.
Parametric Form of a Line
From the vector form we get the coordinates of any point on the line:
\( x = x_1 + a\lambda \)
\( y = y_1 + b\lambda \)
\( z = z_1 + c\lambda \)
- Each value of \( \lambda \) gives a point on the line.
Symmetric (Cartesian) Form of a Line
Eliminate parameter \( \lambda \) from parametric equations. If \( a,\; b,\; c \) are direction ratios, and \( (x_1, y_1, z_1) \) is a known point, then
\( \dfrac{x – x_1}{a} = \dfrac{y – y_1}{b} = \dfrac{z – z_1}{c} \)
Important Points for JEE
- If any direction ratio is zero, that part becomes a constant in symmetric form.
- Direction ratios from symmetric form are simply denominators.
- Two lines are parallel when their DRs are proportional.
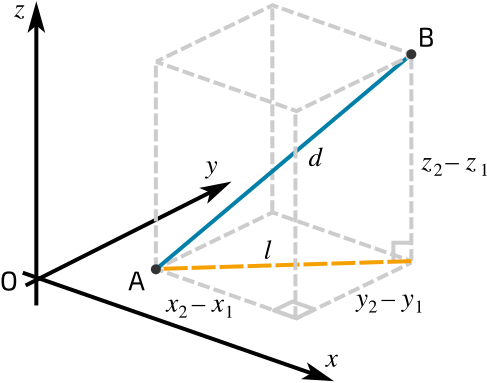
- A line can also be written using two points A and B, with DRs given by \( (x_2 – x_1,\; y_2 – y_1,\; z_2 – z_1) \).
- A line can be rewritten in vector, parametric, or symmetric form as needed.
Line Through Two Points
If a line passes through points \( A(x_1, y_1, z_1) \) and \( B(x_2, y_2, z_2) \), then direction ratios are
\( (a, b, c) = (x_2 – x_1,\; y_2 – y_1,\; z_2 – z_1) \)
Symmetric form becomes
\( \dfrac{x – x_1}{x_2 – x_1} = \dfrac{y – y_1}{y_2 – y_1} = \dfrac{z – z_1}{z_2 – z_1} \)
Example
Find the symmetric form of the line passing through \( A(1, 2, 3) \) with direction ratios \( (2, -1, 4) \).
▶️ Answer / Explanation
Use the standard symmetric form.
\( \dfrac{x – 1}{2} = \dfrac{y – 2}{-1} = \dfrac{z – 3}{4} \)
Example
Find the vector and parametric form of the line passing through two points \( A(2, 3, -1) \) and \( B(5, 11, 2) \).
▶️ Answer / Explanation
First find direction ratios.
\( (a, b, c) = (5 – 2,\; 11 – 3,\; 2 – (-1)) = (3,\; 8,\; 3) \)
Vector form:
\( \vec{r} = (2\hat{i} + 3\hat{j} – \hat{k}) + \lambda(3\hat{i} + 8\hat{j} + 3\hat{k}) \)
Parametric form:
\( x = 2 + 3\lambda \)
\( y = 3 + 8\lambda \)
\( z = -1 + 3\lambda \)
Example
Find the symmetric equation of a line passing through point \( A(4, -2, 1) \) and perpendicular to a line whose symmetric form is \( \dfrac{x – 1}{2} = \dfrac{y + 3}{-1} = \dfrac{z – 5}{3} \).
▶️ Answer / Explanation
The given line has direction ratios:
\( (2, -1, 3) \)
Required line is perpendicular to this line. So its direction ratios must be perpendicular to \( (2, -1, 3) \).
Find a vector \( (a, b, c) \) such that
\( 2a – b + 3c = 0 \)
Choose simple values. Let \( a = 1,\; b = 2 \).
\( 2(1) – 2 + 3c = 0 \Rightarrow 3c = 0 \Rightarrow c = 0 \)
Thus DRs of required line are \( (1, 2, 0) \).
Symmetric form is
\( \dfrac{x – 4}{1} = \dfrac{y + 2}{2} = \dfrac{z – 1}{0} \)
Since denominator of z term is zero, z is constant:
\( z = 1 \)
Thus equation is
\( \dfrac{x – 4}{1} = \dfrac{y + 2}{2},\quad z = 1 \)
Equation of a Plane
A plane in three dimensional geometry is a flat two dimensional surface that extends infinitely. To define a plane uniquely, we need either a point and a normal vector or three non collinear points.
General Form of a Plane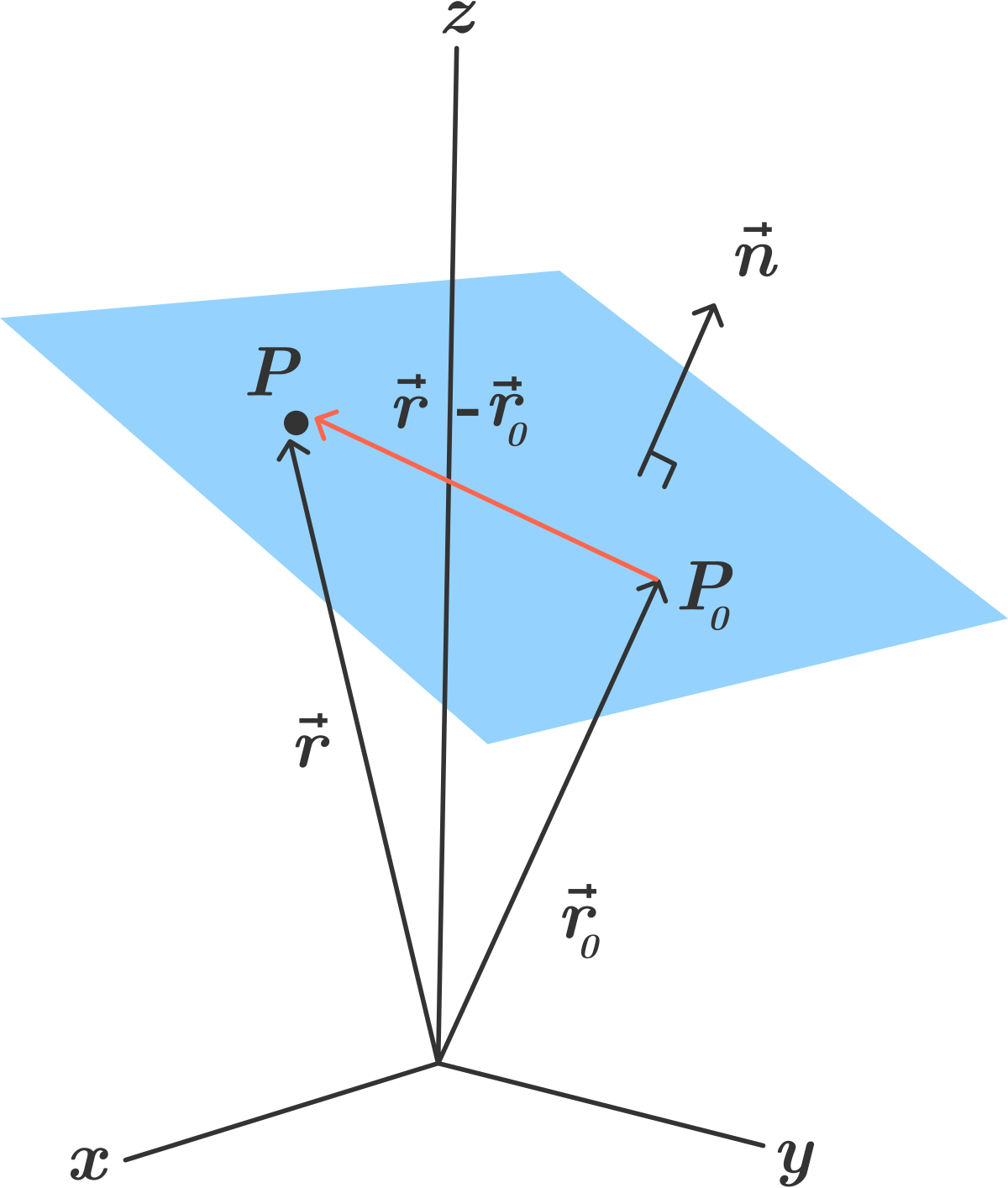
Every plane can be written as
\( ax + by + cz + d = 0 \)
- \( a, b, c \) are the components of the normal vector to the plane.
- \( d \) is a constant.
Vector Form of a Plane
If a plane passes through point \( A(x_1, y_1, z_1) \) and has normal vector \( \vec{n} = a\hat{i} + b\hat{j} + c\hat{k} \), then vector equation is
\( \vec{n} \cdot (\vec{r} – \vec{a}) = 0 \)
This means the vector from point A to any point on the plane is perpendicular to the normal vector.
Cartesian Form (Point Normal Form)
If plane passes through point \( (x_1, y_1, z_1) \) with normal vector \( (a, b, c) \), then
\( a(x – x_1) + b(y – y_1) + c(z – z_1) = 0 \)
Intercept Form of a Plane
If a plane cuts intercepts \( a, b, c \) on the x, y, z axes respectively, then equation is:
\( \dfrac{x}{a} + \dfrac{y}{b} + \dfrac{z}{c} = 1 \)
- If any intercept is infinite, the corresponding term disappears.
Plane Through Three Non Collinear Points
If plane passes through points \( A(x_1, y_1, z_1) \), \( B(x_2, y_2, z_2) \), \( C(x_3, y_3, z_3) \), then
\( \begin{vmatrix} x – x_1 & y – y_1 & z – z_1 \\ x_2 – x_1 & y_2 – y_1 & z_2 – z_1 \\ x_3 – x_1 & y_3 – y_1 & z_3 – z_1 \end{vmatrix} = 0 \)
This determinant ensures that vectors \( \overrightarrow{AB}, \overrightarrow{AC}, \overrightarrow{AP} \) are coplanar.
Important Points for JEE
- Normal vector is perpendicular to entire plane.
- Two planes are parallel if their normal vectors are proportional.
- Two planes are perpendicular if dot product of normals is zero.
- If coefficients \( a, b, c \) are given, you immediately know the normal vector.
Example
Find the equation of a plane passing through \( (2, 1, -3) \) with normal vector \( (1, -2, 4) \).
▶️ Answer / Explanation
Use point normal form.
\( 1(x – 2) – 2(y – 1) + 4(z + 3) = 0 \)
Simplify:
\( x – 2 – 2y + 2 + 4z + 12 = 0 \)
\( x – 2y + 4z + 12 = 0 \)
Example
Find the equation of the plane passing through points \( A(1, 2, 3) \), \( B(2, 3, 1) \), and \( C(3, -1, 4) \).
▶️ Answer / Explanation
Use the determinant form.
\( \begin{vmatrix} x – 1 & y – 2 & z – 3 \\ 2 – 1 & 3 – 2 & 1 – 3 \\ 3 – 1 & -1 – 2 & 4 – 3 \end{vmatrix} = 0 \)
\( \begin{vmatrix} x – 1 & y – 2 & z – 3 \\ 1 & 1 & -2 \\ 2 & -3 & 1 \end{vmatrix} = 0 \)
Expand determinant:
\( (x – 1)(1 \cdot 1 – (-2)(-3)) – (y – 2)(1 \cdot 1 – (-2)(2)) + (z – 3)(1(-3) – 1(2)) = 0 \)
\( (x – 1)(1 – 6) – (y – 2)(1 + 4) + (z – 3)(-3 – 2) = 0 \)
\( -5(x – 1) – 5(y – 2) – 5(z – 3) = 0 \)
Divide by \( -5 \):
\( x + y + z = 6 \)
Example
Find the equation of a plane perpendicular to plane \( 2x – y + 3z = 7 \) and passing through the line of intersection of planes \( x + y + z = 3 \) and \( x – 2y + z = 4 \).
▶️ Answer / Explanation
The line of intersection of planes \( P_1 \) and \( P_2 \) is represented by
\( P_1 + \lambda P_2: \quad (x + y + z – 3) + \lambda(x – 2y + z – 4) = 0 \)
Simplify:
\( (1 + \lambda)x + (1 – 2\lambda)y + (1 + \lambda)z – (3 + 4\lambda) = 0 \)
This is the required plane. We now add the condition that our plane is perpendicular to \( 2x – y + 3z = 7 \).
Normals must satisfy dot product zero.
Normal of required plane: \( (1 + \lambda,\; 1 – 2\lambda,\; 1 + \lambda) \)
Normal of given perpendicular plane: \( (2, -1, 3) \)
Apply dot product:
\( 2(1 + \lambda) – 1(1 – 2\lambda) + 3(1 + \lambda) = 0 \)
\( 2 + 2\lambda – 1 + 2\lambda + 3 + 3\lambda = 0 \)
\( 4 + 7\lambda = 0 \Rightarrow \lambda = -\dfrac{4}{7} \)
Substitute into plane equation.
\( 1 + \lambda = 1 – \dfrac{4}{7} = \dfrac{3}{7} \)
\( 1 – 2\lambda = 1 + \dfrac{8}{7} = \dfrac{15}{7} \)
\( 3 + 4\lambda = 3 – \dfrac{16}{7} = \dfrac{5}{7} \)
Thus plane is:
\( \dfrac{3}{7}x + \dfrac{15}{7}y + \dfrac{3}{7}z – \dfrac{5}{7} = 0 \)
Multiply by 7:
\( 3x + 15y + 3z – 5 = 0 \)
Equation of Line of Intersection of Two Planes
Two non parallel planes intersect in a straight line. To find the equation of this line, we need: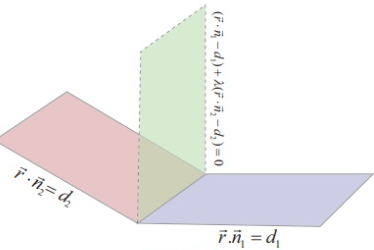
- a point lying on both planes, and
- a direction vector of the line.
Direction Vector of Line of Intersection
If planes are:
\( P_1: a_1 x + b_1 y + c_1 z + d_1 = 0 \)
\( P_2: a_2 x + b_2 y + c_2 z + d_2 = 0 \)
Then their normal vectors are:
\( \vec{n_1} = (a_1, b_1, c_1),\quad \vec{n_2} = (a_2, b_2, c_2) \)
The direction vector of the line of intersection is:
\( \vec{d} = \vec{n_1} \times \vec{n_2} \)
- Cross product of normals gives a vector perpendicular to both normals, meaning it lies along the intersection line.
Finding a Point on the Line
To find a common point of the two planes:
- Set one variable to a convenient value (usually \( z = 0 \) or \( y = 0 \)).
- Solve the two plane equations simultaneously.
- If it fails, choose another value for free variable.
Final Line Equation (Parametric Form)
If a point on intersection is \( (x_0, y_0, z_0) \) and direction vector is \( (p, q, r) \), then
\( x = x_0 + p\lambda,\quad y = y_0 + q\lambda,\quad z = z_0 + r\lambda \)
Symmetric Form
\( \dfrac{x – x_0}{p} = \dfrac{y – y_0}{q} = \dfrac{z – z_0}{r} \)
Example
Find the line of intersection of planes \( x + y + z = 6 \) and \( x – y + z = 2 \).
▶️ Answer / Explanation
Step 1: Direction vector
Normals:
\( \vec{n_1} = (1, 1, 1) \), \( \vec{n_2} = (1, -1, 1) \)
Cross product:
\( \vec{d} = \begin{vmatrix} \hat{i} & \hat{j} & \hat{k} \\ 1 & 1 & 1 \\ 1 & -1 & 1 \end{vmatrix} \)
\( = \hat{i}(1\cdot1 – 1(-1)) – \hat{j}(1\cdot1 – 1\cdot1) + \hat{k}(1(-1) – 1\cdot1) \)
\( = \hat{i}(1 + 1) – \hat{j}(1 – 1) + \hat{k}(-1 – 1) \)
\( = (2, 0, -2) = (1, 0, -1) \)
Step 2: Find a point on both planes
Set \( z = 0 \).
From first plane: \( x + y = 6 \)
From second plane: \( x – y = 2 \)
Add:
\( 2x = 8 \Rightarrow x = 4 \)
\( y = 2 \)
Point = \( (4, 2, 0) \)
Line equation:
\( x = 4 + \lambda,\quad y = 2,\quad z = -\lambda \)
Example
Find the line of intersection of planes \( 2x – y + 3z = 5 \) and \( x + 4y – z = 3 \).
▶️ Answer / Explanation
Step 1: Direction vector
Normals:
\( \vec{n_1} = (2, -1, 3) \), \( \vec{n_2} = (1, 4, -1) \)
Cross product:
\( \vec{d} = \begin{vmatrix} \hat{i} & \hat{j} & \hat{k} \\ 2 & -1 & 3 \\ 1 & 4 & -1 \end{vmatrix} \)
\( = \hat{i}((-1)(-1) – 3\cdot4) – \hat{j}(2(-1) – 3\cdot1) + \hat{k}(2\cdot4 – (-1)1) \)
\( = \hat{i}(1 – 12) – \hat{j}(-2 – 3) + \hat{k}(8 + 1) \)
\( = (-11, 5, 9) \)
Step 2: Point on both planes
Try \( z = 0 \).
\( 2x – y = 5 \) \( x + 4y = 3 \)
Solve simultaneously:
Multiply second equation by 2:
\( 2x + 8y = 6 \)
Subtract from first equation:
\( -9y = -1 \Rightarrow y = \dfrac{1}{9} \)
\( x = \dfrac{5 + y}{2} = \dfrac{5 + 1/9}{2} = \dfrac{46}{18} = \dfrac{23}{9} \)
Point = \( \left( \dfrac{23}{9}, \dfrac{1}{9}, 0 \right) \)
Line equation:
\( x = \dfrac{23}{9} – 11\lambda,\quad y = \dfrac{1}{9} + 5\lambda,\quad z = 9\lambda \)
Example
Find the line of intersection of planes \( x + 2y – 2z + 3 = 0 \) and \( 3x – y + z – 4 = 0 \). Express your answer in symmetric form.
▶️ Answer / Explanation
Step 1: Find direction vector.
Normals:
\( \vec{n_1} = (1, 2, -2) \)
\( \vec{n_2} = (3, -1, 1) \)
Cross product:
\( \vec{d} = \begin{vmatrix} \hat{i} & \hat{j} & \hat{k} \\ 1 & 2 & -2 \\ 3 & -1 & 1 \end{vmatrix} \)
\( = \hat{i}(2\cdot1 – (-2)(-1)) – \hat{j}(1\cdot1 – (-2)3) + \hat{k}(1(-1) – 2\cdot3) \)
\( = \hat{i}(2 – 2) – \hat{j}(1 + 6) + \hat{k}(-1 – 6) \)
\( = (0, -7, -7) = (0, 1, 1) \)
Step 2: Find a point on the intersection.
Set \( x = 0 \).
First plane: \( 2y – 2z + 3 = 0 \Rightarrow y – z = -\dfrac{3}{2} \)
Second plane: \( -y + z – 4 = 0 \Rightarrow y – z = -4 \)
Contradiction, so choose \( z = 0 \).
First plane: \( x + 2y + 3 = 0 \Rightarrow x = -2y – 3 \)
Second plane: \( 3x – y – 4 = 0 \)
Substitute:
\( 3(-2y – 3) – y – 4 = 0 \)
\( -6y – 9 – y – 4 = 0 \Rightarrow -7y = 13 \Rightarrow y = -\dfrac{13}{7} \)
\( x = -2\left( -\dfrac{13}{7} \right) – 3 = \dfrac{26}{7} – 3 = \dfrac{5}{7} \)
Point = \( \left( \dfrac{5}{7}, -\dfrac{13}{7}, 0 \right) \)
Step 3: Symmetric form of intersection line.
Direction vector = \( (0, 1, 1) \).
Symmetric form:
\( x = \dfrac{5}{7} \)
\( \dfrac{y + 13/7}{1} = \dfrac{z – 0}{1} \)
Thus:
\( x = \dfrac{5}{7},\quad \dfrac{y + \dfrac{13}{7}}{1} = \dfrac{z}{1} \)
