IIT JEE Main Maths -Unit 1- Relations: types and properties- Study Notes-New Syllabus
IIT JEE Main Maths -Unit 1- Relations: types and properties – Study Notes – New syllabus
IIT JEE Main Maths -Unit 1- Relations: types and properties – Study Notes -IIT JEE Main Maths – per latest Syllabus.
Key Concepts:
- Relation
- Domain, Co-domain, and Range
- Representation of Relation
- Types of Relations
Cartesian Product of Sets
If \( A \) and \( B \) are two non-empty sets, then the Cartesian product of \( A \) and \( B \), denoted by \( A \times B \), is the set of all ordered pairs \( (a, b) \) such that \( a \in A \) and \( b \in B \).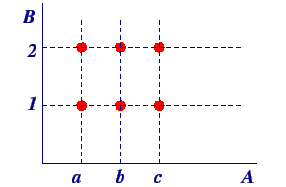
\( A \times B = \{(a,b) \mid a \in A, \, b \in B\} \)
The number of elements in \( A \times B \) is given by:
\( n(A \times B) = n(A) \times n(B) \)
Note: The order of elements in each pair matters. In general, \( A \times B \ne B \times A \).
Example
Let \( A = \{1, 2\} \) and \( B = \{x, y, z\} \). Find \( A \times B \) and \( B \times A \).
▶️ Answer / Explanation
Step 1: Form all possible ordered pairs \( (a,b) \) where \( a \in A \) and \( b \in B \).
\( A \times B = \{(1,x), (1,y), (1,z), (2,x), (2,y), (2,z)\} \)
Step 2: Reverse the order for \( B \times A \).
\( B \times A = \{(x,1), (x,2), (y,1), (y,2), (z,1), (z,2)\} \)
Conclusion: \( A \times B \ne B \times A \).
Relation
A relation from set \( A \) to set \( B \) is any subset of the Cartesian product \( A \times B \).
\( R \subseteq A \times B \)
If \( (a, b) \in R \), we say that \( a \) is related to \( b \) under the relation \( R \), and we write it as \( a \, R \, b \).
Example: If \( A = \{1, 2, 3\} \) and \( B = \{1, 4, 9\} \), a relation \( R \) can be defined by “\( b = a^2 \)”. Then, \( R = \{(1,1), (2,4), (3,9)\} \).
Thus, a relation describes how elements of one set are associated with elements of another set.
Example
Let \( A = \{2, 4, 6\} \) and \( B = \{1, 2, 3, 4, 5, 6\} \). Define a relation \( R \) from \( A \) to \( B \) as “\( a \) divides \( b \)”. Write \( R \).
▶️ Answer / Explanation
Step 1: For each \( a \in A \), find all \( b \in B \) such that \( b \) is divisible by \( a \).
- For \( a = 2 \): \( b = 2, 4, 6 \)
- For \( a = 4 \): \( b = 4 \)
- For \( a = 6 \): \( b = 6 \)
Step 2: Write the set of ordered pairs.
\( R = \{(2,2), (2,4), (2,6), (4,4), (6,6)\} \)
Step 3: Verify definition.
Each pair \( (a,b) \) satisfies \( a \) divides \( b \).
Conclusion: \( R \subseteq A \times B \) is a valid relation defined by “divides”.
Domain, Co-domain, and Range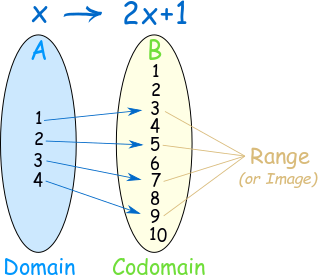
For a relation \( R \) from set \( A \) to set \( B \), i.e., \( R \subseteq A \times B \):
- Domain: The set of all first elements of the ordered pairs in \( R \). \( \text{Domain}(R) = \{a \mid (a,b) \in R\} \)
- Co-domain: The set \( B \), i.e., the second set from which elements of ordered pairs are taken.
- Range: The set of all second elements of the ordered pairs in \( R \). \( \text{Range}(R) = \{b \mid (a,b) \in R\} \)
Note: Range \( \subseteq \) Co-domain
Example
For the relation \( R = \{(1,1), (2,4), (3,9)\} \) from \( A = \{1, 2, 3\} \) to \( B = \{1, 4, 9, 16\} \), find the domain, co-domain, and range.
▶️ Answer / Explanation
Step 1: Identify sets \( A \) and \( B \).
\( A = \{1, 2, 3\} \), \( B = \{1, 4, 9, 16\} \)
Step 2: Find domain and range.
Domain = \( \{1, 2, 3\} \)
Range = \( \{1, 4, 9\} \)
Step 3: Co-domain = \( \{1, 4, 9, 16\} \)
Step 4: Verify that Range \( \subseteq \) Co-domain.
Conclusion: Domain represents inputs, Co-domain represents all possible outputs, and Range represents actual outputs related through \( R \).
Representation of Relation
A relation from a set \( A \) to a set \( B \) can be represented in different forms for better understanding. The most common methods are:
Roster (Tabular) Form:![]()
In this method, the relation is represented by listing all the ordered pairs explicitly.
Example: If \( A = \{1, 2, 3\} \) and \( B = \{2, 4, 6\} \), and \( R = \{(1,2), (2,4), (3,6)\} \), this is the roster form of relation \( R \).
Set-builder Form:
In this form, a common property is described that all ordered pairs satisfy.
Example: \( R = \{(a,b) \mid b = 2a,\, a \in A,\, b \in B\} \)
Arrow (Pictorial) Diagram:
In this representation, elements of set \( A \) and \( B \) are written in two ovals. Arrows are drawn from each element of \( A \) to its related elements in \( B \).
Example: For \( R = \{(1,a), (1,d), (2,b), (3,c)\} \):
- An arrow from 1 → a
- An arrow from 1 → d
- An arrow from 2 → b
- An arrow from 3 → c represent the relation pictorially.
Example
Let \( A = \{1, 2, 3\} \) and \( B = \{1, 2, 3\} \). Define a relation \( R \) from \( A \) to \( B \) as “\( a \) is less than \( b \)”. Represent \( R \) in roster and matrix form.
▶️ Answer / Explanation
Step 1: List all ordered pairs where \( a < b \).
\( R = \{(1,2), (1,3), (2,3)\} \)
Step 2: Write in matrix form.
Since \( A = B = \{1,2,3\} \), both have 3 elements.
| A\B | 1 | 2 | 3 |
|---|---|---|---|
| 1 | 0 | 1 | 1 |
| 2 | 0 | 0 | 1 |
| 3 | 0 | 0 | 0 |
Step 3: Interpretation:
‘1’ in position \( (i,j) \) shows that \( a_i < b_j \). For example, \( (1,2) \) and \( (2,3) \) have 1s indicating true relations.
Conclusion: The relation \( R = \{(1,2), (1,3), (2,3)\} \) is represented by the above 3×3 matrix.
Types of Relations
A relation on a set \( A \) is a subset of \( A \times A \). Depending on the properties it satisfies, a relation can be classified as Reflexive, Identity, Symmetric, Transitive, Antisymmetric, Equivalence, or Inverse relation.
Reflexive Relation
A relation \( R \) on a set \( A \) is said to be reflexive if every element of \( A \) is related to itself.
That is, \( (a,a) \in R \) for all \( a \in A \).
Mathematically: \( \forall a \in A,\, (a,a) \in R \).
Example
Let \( A = \{1,2,3\} \) and \( R = \{(1,1), (2,2), (3,3)\} \).Describe the type of Relation.
▶️ Explanation
Each element is related to itself, so \( R \) is reflexive on \( A \).
Identity Relation
The identity relation on a set \( A \) is the relation that contains only pairs where both elements are the same.
It is denoted by \( I_A = \{(a,a) \mid a \in A\} \).
Every identity relation is reflexive.
Example
If \( A = \{x, y, z\} \), then \( I_A = \{(x,x), (y,y), (z,z)\} \).Describe the type of Relation.
▶️ Explanation
This relation includes only pairs of the form \( (a,a) \), hence it’s the identity relation on \( A \).
Symmetric Relation
A relation \( R \) on \( A \) is symmetric if for every \( (a,b) \in R \), we also have \( (b,a) \in R \).
Mathematically: \( \forall a,b \in A,\ (a,b) \in R \Rightarrow (b,a) \in R \).
Example
Let \( A = \{1,2,3\} \) and \( R = \{(1,2), (2,1), (2,3), (3,2)\} \).Describe the type of Relation.
▶️ Explanation
For every pair \( (a,b) \), the pair \( (b,a) \) is also present. Hence, \( R \) is symmetric.
Transitive Relation
A relation \( R \) on \( A \) is transitive if whenever \( (a,b) \in R \) and \( (b,c) \in R \), then \( (a,c) \in R \).
Mathematically: \( \forall a,b,c \in A,\ (a,b) \in R \text{ and } (b,c) \in R \Rightarrow (a,c) \in R \).
Example
Let \( A = \{1,2,3\} \) and \( R = \{(1,2), (2,3), (1,3)\} \).Describe the type of Relation.
▶️ Explanation
Since \( (1,2) \) and \( (2,3) \) imply \( (1,3) \) is in \( R \), the relation is transitive.
Antisymmetric Relation
A relation \( R \) on \( A \) is antisymmetric if for all \( a,b \in A \), \( (a,b) \in R \) and \( (b,a) \in R \) together imply \( a = b \).
Mathematically: \( (a,b) \in R \text{ and } (b,a) \in R \Rightarrow a = b \).
Example
Let \( A = \{1,2,3\} \) and \( R = \{(1,1), (2,2), (3,3), (1,2)\} \).Describe the type of Relation.
▶️ Explanation
\( (1,2) \in R \), but \( (2,1) \notin R \). Only equal pairs like \( (1,1), (2,2), (3,3) \) have both directions, so \( R \) is antisymmetric.
Equivalence Relation
A relation \( R \) on \( A \) is an equivalence relation if it is:
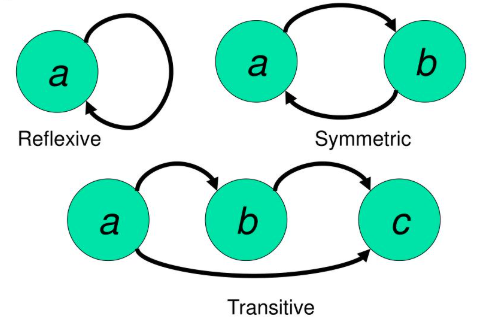
- Reflexive
- Symmetric
- Transitive
Equivalence relations partition a set into disjoint subsets called equivalence classes.
Example
Let \( A = \mathbb{Z} \) and define \( R = \{(a,b) \mid a – b \text{ is divisible by } 5\} \). Describe the type of Relation.
▶️ Explanation
Reflexive: \( a – a = 0 \) is divisible by 5.
Symmetric: If \( a – b \) divisible by 5, then \( b – a \) is also divisible by 5.
Transitive: If \( a – b \) and \( b – c \) divisible by 5, then \( a – c \) is divisible by 5.
Hence, \( R \) is an equivalence relation.
Inverse Relation
If \( R \) is a relation from set \( A \) to set \( B \), then the inverse relation \( R^{-1} \) is the relation from \( B \) to \( A \) defined as:
\( R^{-1} = \{(b,a) \mid (a,b) \in R\} \).
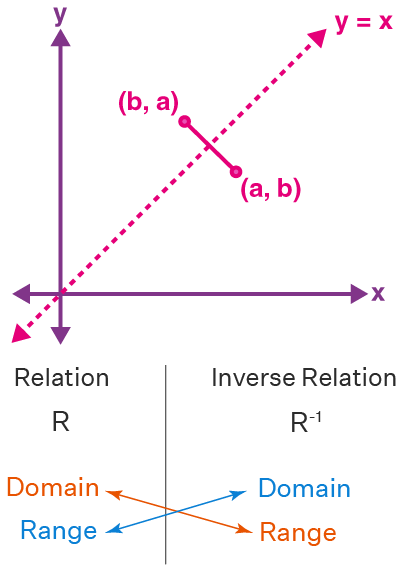
That is, all ordered pairs in \( R \) are reversed in \( R^{-1} \).
Example
Let \( R = \{(1,2), (2,3), (3,4)\} \).Find its Inverse Relation.
▶️ Explanation
Then \( R^{-1} = \{(2,1), (3,2), (4,3)\} \). The direction of relation is reversed.
