IIT JEE Main Maths -Unit 11- Skew lines and shortest distance between them- Study Notes-New Syllabus
IIT JEE Main Maths -Unit 11- Skew lines and shortest distance between them – Study Notes – New syllabus
IIT JEE Main Maths -Unit 11- Skew lines and shortest distance between them – Study Notes -IIT JEE Main Maths – per latest Syllabus.
Key Concepts:
- Shortest Distance Between Two Skew Lines
Shortest Distance Between Two Skew Lines
Two lines in 3D are called skew if they are neither parallel nor intersecting. The shortest distance (SD) between two skew lines is the length of the common perpendicular drawn between them.
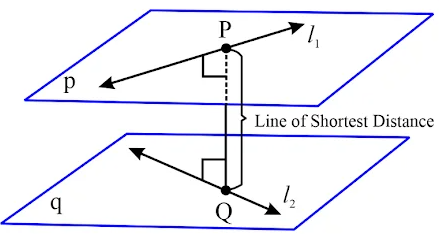
Lines in Vector Form
Let two lines be
Line 1: \( \vec{r} = \vec{a_1} + \lambda \vec{b_1} \)
Line 2: \( \vec{r} = \vec{a_2} + \mu \vec{b_2} \)
- \( \vec{a_1}, \vec{a_2} \) are position vectors of points on the lines.
- \( \vec{b_1}, \vec{b_2} \) are direction vectors.
Formula for Shortest Distance
The shortest distance between the two skew lines is given by
\( \text{SD} = \dfrac{|(\vec{a_2} – \vec{a_1}) \cdot (\vec{b_1} \times \vec{b_2})|}{|\vec{b_1} \times \vec{b_2}|} \)
Explanation of formula
- \( \vec{b_1} \times \vec{b_2} \) gives the direction of the common perpendicular.
- The scalar triple product gives volume of parallelepiped.
- Dividing volume by area of base gives height, which is the shortest distance.
Special Cases
- If \( \vec{b_1} \times \vec{b_2} = 0 \) then lines are parallel.
- If lines intersect, SD = 0.
Using Cartesian Form
If lines are
\( \dfrac{x – x_1}{a_1} = \dfrac{y – y_1}{b_1} = \dfrac{z – z_1}{c_1} \)
\( \dfrac{x – x_2}{a_2} = \dfrac{y – y_2}{b_2} = \dfrac{z – z_2}{c_2} \)
then
\( \vec{b_1} = (a_1, b_1, c_1),\quad \vec{b_2} = (a_2, b_2, c_2) \)
and
\( \vec{a_2} – \vec{a_1} = (x_2 – x_1,\; y_2 – y_1,\; z_2 – z_1) \)
Example
Find the shortest distance between the lines \( \dfrac{x}{1} = \dfrac{y}{2} = \dfrac{z}{3} \) and \( \dfrac{x – 2}{2} = \dfrac{y – 1}{1} = \dfrac{z – 3}{2} \).
▶️ Answer / Explanation
Direction vectors:
\( \vec{b_1} = (1, 2, 3),\quad \vec{b_2} = (2, 1, 2) \)
Point vectors:
\( \vec{a_1} = (0, 0, 0),\quad \vec{a_2} = (2, 1, 3) \)
Compute difference:
\( \vec{a_2} – \vec{a_1} = (2, 1, 3) \)
Compute cross product:
\( \vec{b_1} \times \vec{b_2} = \begin{vmatrix} \hat{i} & \hat{j} & \hat{k} \\ 1 & 2 & 3 \\ 2 & 1 & 2 \end{vmatrix} \)
\( = \hat{i}(2\cdot2 – 3\cdot1) – \hat{j}(1\cdot2 – 3\cdot2) + \hat{k}(1\cdot1 – 2\cdot2) \)
\( = \hat{i}(4 – 3) – \hat{j}(2 – 6) + \hat{k}(1 – 4) \)
\( = (1, 4, -3) \)
Scalar triple product:
\( (2, 1, 3) \cdot (1, 4, -3) = 2 + 4 – 9 = -3 \)
Absolute = 3.
Magnitude of cross product:
\( \sqrt{1^2 + 4^2 + (-3)^2} = \sqrt{26} \)
Shortest distance:
\( \text{SD} = \dfrac{3}{\sqrt{26}} \)
Example
Find the shortest distance between the lines \( \vec{r} = (1, 2, 3) + \lambda(2, -1, 2) \) and \( \vec{r} = (3, 1, 4) + \mu(1, 2, -2) \).
▶️ Answer / Explanation
\( \vec{a_1} = (1, 2, 3),\quad \vec{a_2} = (3, 1, 4) \)
\( \vec{b_1} = (2, -1, 2),\quad \vec{b_2} = (1, 2, -2) \)
\( \vec{a_2} – \vec{a_1} = (2, -1, 1) \)
Cross product:
\( \vec{b_1} \times \vec{b_2} = \begin{vmatrix} \hat{i} & \hat{j} & \hat{k} \\ 2 & -1 & 2 \\ 1 & 2 & -2 \end{vmatrix} \)
\( = \hat{i}((-1)(-2) – 2\cdot2) – \hat{j}(2(-2) – 2\cdot1) + \hat{k}(2\cdot2 – (-1)1) \)
\( = \hat{i}(2 – 4) – \hat{j}(-4 – 2) + \hat{k}(4 + 1) \)
\( = (-2, 6, 5) \)
Scalar triple product:
\( (2, -1, 1) \cdot (-2, 6, 5) = -4 – 6 + 5 = -5 \)
Absolute = 5.
Magnitude:
\( \sqrt{(-2)^2 + 6^2 + 5^2} = \sqrt{4 + 36 + 25} = \sqrt{65} \)
SD = \( \dfrac{5}{\sqrt{65}} \).
Example
Find the shortest distance between the lines \( \dfrac{x – 1}{3} = \dfrac{y + 2}{1} = \dfrac{z – 4}{2} \) and \( \dfrac{x – 3}{1} = \dfrac{y – 1}{2} = \dfrac{z}{3} \).
▶️ Answer / Explanation
Direction vectors:
\( \vec{b_1} = (3, 1, 2),\quad \vec{b_2} = (1, 2, 3) \)
Points:
\( A(1, -2, 4),\quad B(3, 1, 0) \)
\( \vec{a_2} – \vec{a_1} = (2, 3, -4) \)
Cross product:
\( \vec{b_1} \times \vec{b_2} = \begin{vmatrix} \hat{i} & \hat{j} & \hat{k} \\ 3 & 1 & 2 \\ 1 & 2 & 3 \end{vmatrix} \)
\( = \hat{i}(1\cdot3 – 2\cdot2) – \hat{j}(3\cdot3 – 2\cdot1) + \hat{k}(3\cdot2 – 1\cdot1) \)
\( = \hat{i}(3 – 4) – \hat{j}(9 – 2) + \hat{k}(6 – 1) \)
\( = (-1, -7, 5) \)
Scalar triple product:
\( (2, 3, -4) \cdot (-1, -7, 5) = -2 – 21 – 20 = -43 \)
Absolute = 43.
Magnitude:
\( \sqrt{(-1)^2 + (-7)^2 + 5^2} = \sqrt{1 + 49 + 25} = \sqrt{75} = 5\sqrt{3} \)
Shortest Distance:
\( \text{SD} = \dfrac{43}{5\sqrt{3}} \)
