IIT JEE Main Maths -Unit 10- Angle between two lines- Study Notes-New Syllabus
IIT JEE Main Maths -Unit 10- Angle between two lines – Study Notes – New syllabus
IIT JEE Main Maths -Unit 10- Angle between two lines – Study Notes -IIT JEE Main Maths – per latest Syllabus.
Key Concepts:
- Angle Between Two Lines
Angle Between Two Lines
In 3D geometry, each line has a direction represented by a direction vector or direction ratios (d.r.s). The angle between two lines is defined as the angle between their direction vectors.
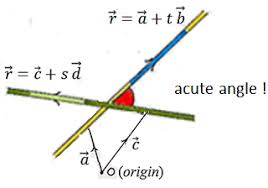
Angle Between Two Lines Using Direction Ratios
If line \( L_1 \) has direction ratios \( (a_1, b_1, c_1) \) and line \( L_2 \) has direction ratios \( (a_2, b_2, c_2) \), then the angle \( \theta \) between them is given by:
\( \cos\theta = \dfrac{a_1a_2 + b_1b_2 + c_1c_2}{\sqrt{a_1^2 + b_1^2 + c_1^2}\sqrt{a_2^2 + b_2^2 + c_2^2}} \)
- This formula is identical to the dot product formula.
- Use absolute value when asked for acute angle: \( \cos\theta = \left| \dfrac{\vec{d_1} \cdot \vec{d_2}}{|\vec{d_1}| |\vec{d_2}|} \right| \)
Angle Between Two Lines in Symmetric Form
If lines are:
\( L_1: \dfrac{x – x_1}{a_1} = \dfrac{y – y_1}{b_1} = \dfrac{z – z_1}{c_1} \)
\( L_2: \dfrac{x – x_2}{a_2} = \dfrac{y – y_2}{b_2} = \dfrac{z – z_2}{c_2} \)
Then direction ratios are simply:
- For \( L_1 \): \( (a_1, b_1, c_1) \)
- For \( L_2 \): \( (a_2, b_2, c_2) \)
Use same formula.
Angle Between Lines in Vector Form
If direction vectors are
- \( \vec{d_1} = \langle l_1, m_1, n_1 \rangle \)
- \( \vec{d_2} = \langle l_2, m_2, n_2 \rangle \)
Then
\( \cos\theta = \dfrac{\vec{d_1} \cdot \vec{d_2}}{|\vec{d_1}| |\vec{d_2}|} \)
Special Cases
- Lines are perpendicular if \( a_1a_2 + b_1b_2 + c_1c_2 = 0 \)
- Lines are parallel if \( \dfrac{a_1}{a_2} = \dfrac{b_1}{b_2} = \dfrac{c_1}{c_2} \)
Example
Find the angle between two lines whose direction ratios are \( L_1: (1, 2, 2) \) and \( L_2: (2, 1, 2) \).
▶️ Answer / Explanation
Use formula:
\( \cos\theta = \dfrac{1\cdot 2 + 2\cdot 1 + 2\cdot 2}{\sqrt{1^2 + 2^2 + 2^2}\sqrt{2^2 + 1^2 + 2^2}} \)
\( = \dfrac{2 + 2 + 4}{\sqrt{9}\sqrt{9}} = \dfrac{8}{3 \cdot 3} = \dfrac{8}{9} \)
\( \theta = \cos^{-1}\left(\dfrac{8}{9}\right) \)
Answer: \( \theta = \cos^{-1}\left(\dfrac{8}{9}\right) \)
Example
Find the acute angle between the lines:
\( L_1: \dfrac{x}{2} = \dfrac{y}{3} = \dfrac{z}{6} \)
\( L_2: \dfrac{x}{1} = \dfrac{y}{2} = \dfrac{z}{3} \)
▶️ Answer / Explanation
Direction ratios:
- L1 → (2, 3, 6)
- L2 → (1, 2, 3)
\( \cos\theta = \dfrac{2\cdot 1 + 3\cdot 2 + 6\cdot 3}{\sqrt{4 + 9 + 36}\sqrt{1 + 4 + 9}} \)
= \( \dfrac{2 + 6 + 18}{\sqrt{49}\sqrt{14}} = \dfrac{26}{7\sqrt{14}} \)
\( \theta = \cos^{-1}\left(\dfrac{26}{7\sqrt{14}}\right) \)
Answer: \( \theta = \cos^{-1}\left(\dfrac{26}{7\sqrt{14}}\right) \)
Example
Find the angle between lines given in vector form:
\( \vec{r} = (1,2,3) + \lambda(2, -1, 2) \)
\( \vec{r} = (3,0,1) + \mu(1, 2, -2) \)
▶️ Answer / Explanation
Direction vectors:
- \( \vec{d_1} = (2, -1, 2) \)
- \( \vec{d_2} = (1, 2, -2) \)
Dot product:
\( \vec{d_1} \cdot \vec{d_2} = 2\cdot 1 + (-1)\cdot 2 + 2\cdot (-2) = 2 – 2 – 4 = -4 \)
\( |\vec{d_1}| = \sqrt{2^2 + (-1)^2 + 2^2} = 3 \)
\( |\vec{d_2}| = \sqrt{1^2 + 2^2 + (-2)^2} = 3 \)
\( \cos\theta = \dfrac{-4}{9} \)
\( \theta = \cos^{-1}\left(-\dfrac{4}{9}\right) \)
Answer: \( \theta = \cos^{-1}\left(-\dfrac{4}{9}\right) \)
