IIT JEE Main Maths -Unit 10- Auxiliary circle and related properties- Study Notes-New Syllabus
IIT JEE Main Maths -Unit 10- Auxiliary circle and related properties – Study Notes – New syllabus
IIT JEE Main Maths -Unit 10- Auxiliary circle and related properties – Study Notes -IIT JEE Main Maths – per latest Syllabus.
Key Concepts:
- Ellipse: Auxiliary Circle and Related Properties
- Ellipse: Director Circle
- Ellipse: Chord of Contact
- Ellipse: Pair of Tangents
Ellipse: Auxiliary Circle and Related Properties
The auxiliary circle is a very important geometric tool used in ellipse problems involving parametric form, tangents, normals, eccentric angles, and chord problems.
Standard ellipse:
\( \dfrac{x^2}{a^2}+\dfrac{y^2}{b^2}=1,\quad a > b > 0 \)
1. Definition of Auxiliary Circle
The auxiliary circle of the ellipse is the circle: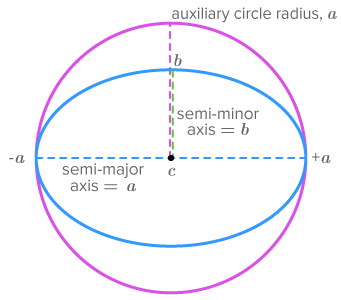
\( x^2 + y^2 = a^2 \)
It has:
- Center at origin (same as ellipse)
- Radius = semi-major axis \( a \)
The auxiliary circle is used to relate circular angles to ellipse points.
2. Parametric Representation Using Auxiliary Circle
A point on the auxiliary circle is:
\( (a\cos\theta,\ a\sin\theta) \)
This corresponds to a point on the ellipse:
\( (x,y) = (a\cos\theta,\ b\sin\theta) \)
\(\theta\) is called the eccentric angle of the ellipse.
This gives the most important ellipse parametrisation:
\( x = a\cos\theta,\quad y = b\sin\theta \)
Almost every JEE tangent-normal question uses eccentric angle.
3. Relationship Between Auxiliary Circle and Tangent
Using eccentric angle, tangent at \((a\cos\theta,\ b\sin\theta)\) is written as:
\( \dfrac{x\cos\theta}{a} + \dfrac{y\sin\theta}{b} = 1 \)
Note:
- Tangent is linear in cosθ and sinθ → simplifies many geometric problems.
- Graphical representation comes from projection of the tangent from auxiliary circle onto ellipse.
4. Relationship Between Auxiliary Circle and Normal
Normal at the parametric point is:
\( a x \sec\theta – b y \csc\theta = a^2 – b^2 \)
This also comes from differentiating the parametric representation derived using the auxiliary circle.
5. Area Property
The parametric form helps in evaluating many ellipse integrals.
Area swept by radius vector in auxiliary circle projects down to ellipse and scales by:
\( \text{Scaling factor} = \dfrac{b}{a} \)
6. Using Auxiliary Circle to Compute Chord Lengths
If two points correspond to eccentric angles \( \theta_1 \) and \( \theta_2 \):
Chord length formula using auxiliary circle:
\( PQ = \sqrt{a^2(\cos\theta_1 – \cos\theta_2)^2 + b^2(\sin\theta_1 – \sin\theta_2)^2} \)
Special case: chord through center (diameter):
\( \theta_2 = \theta_1 + \pi \)
Then \( PQ = 2a|\cos\theta_1| \) or \( PQ = 2b|\sin\theta_1| \)
7. Property: Mapping Circle Angles to Ellipse Eccentric Angles
Angle measured on auxiliary circle = eccentric angle \( \theta \). This angle does not represent the geometric polar angle of the ellipse point.
For ellipse point \( (x,y) \):
\( \tan\phi = \dfrac{y}{x} = \dfrac{b\sin\theta}{a\cos\theta} \)
Thus:
\( \tan\phi = \dfrac{b}{a}\tan\theta \)
So polar angle \( \phi \) is compressed relative to \( \theta \).
Example
Write the auxiliary circle of the ellipse \( \dfrac{x^2}{36}+\dfrac{y^2}{16}=1. \)
▶️ Answer / Explanation
Here \( a^2 = 36 \Rightarrow a = 6 \).
Auxiliary circle:
\( x^2 + y^2 = a^2 = 36 \)
Answer: \( x^2 + y^2 = 36 \)
Example
For the ellipse \( \dfrac{x^2}{25}+\dfrac{y^2}{9}=1, \) find the coordinates of the point corresponding to eccentric angle \( \theta = \dfrac{\pi}{4} \).
▶️ Answer / Explanation
Parametric form:
\( x = a\cos\theta,\ y = b\sin\theta \)
\( a = 5,\ b = 3 \)
\( x = 5\cos\dfrac{\pi}{4} = \dfrac{5}{\sqrt{2}} \)
\( y = 3\sin\dfrac{\pi}{4} = \dfrac{3}{\sqrt{2}} \)
Answer: \( \left(\dfrac{5}{\sqrt{2}},\ \dfrac{3}{\sqrt{2}}\right) \)
Example
Find the length of chord joining two ellipse points having eccentric angles \( \theta = \dfrac{\pi}{6} \) and \( \theta = \dfrac{\pi}{3} \) for ellipse \( \dfrac{x^2}{a^2}+\dfrac{y^2}{b^2}=1. \)
▶️ Answer / Explanation
Chord length formula:
\( PQ = \sqrt{a^2(\cos\theta_1 – \cos\theta_2)^2 + b^2(\sin\theta_1 – \sin\theta_2)^2} \)
Compute values:
\( \cos\frac{\pi}{6} = \frac{\sqrt{3}}{2},\quad \cos\frac{\pi}{3} = \frac{1}{2} \)
\( \sin\frac{\pi}{6} = \frac{1}{2},\quad \sin\frac{\pi}{3} = \frac{\sqrt{3}}{2} \)
Difference in x-terms: \( \frac{\sqrt{3}}{2} – \frac{1}{2} = \frac{\sqrt{3}-1}{2} \)
Difference in y-terms: \( \frac{1}{2} – \frac{\sqrt{3}}{2} = \frac{1 – \sqrt{3}}{2} \)
Now length:
\( PQ = \sqrt{\, a^2\left(\dfrac{\sqrt{3}-1}{2}\right)^2 + b^2\left(\dfrac{1-\sqrt{3}}{2}\right)^2 } \)
\( = \left|\dfrac{\sqrt{3}-1}{2}\right|\sqrt{a^2 + b^2} \)
Answer: \( PQ = \dfrac{|\sqrt{3}-1|}{2}\sqrt{a^2 + b^2} \)
Ellipse: Director Circle
The director circle of an ellipse is the locus of the point from which two perpendicular tangents can be drawn to the ellipse.
For ellipse:
\( \dfrac{x^2}{a^2}+\dfrac{y^2}{b^2}=1 \)
1. Condition for Perpendicular Tangents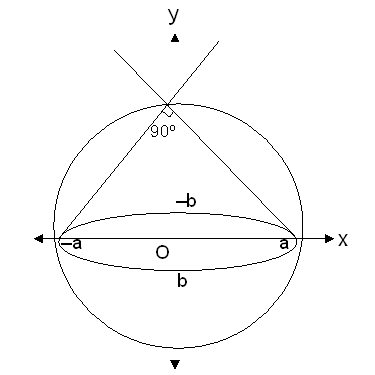
Slope form of tangent to the ellipse:
\( y = mx \pm \sqrt{a^2 m^2 + b^2} \)
Two tangents from a point are perpendicular if:
\( m_1 m_2 = -1 \)
Using tangent equation and condition, after algebraic elimination we obtain locus.
2. Director Circle Equation
For ellipse:
\( \dfrac{x^2}{a^2}+\dfrac{y^2}{b^2}=1 \)
The director circle is:
\( x^2 + y^2 = a^2 + b^2 \)
This is a circle centered at the origin with radius \( \sqrt{a^2 + b^2} \).
3. When Does Director Circle Exist?
- If \( a = b \) (i.e., the ellipse becomes a circle), director circle = actual circle.
- If \( a \ne b \), director circle always exists.
- Geometrically, it is the boundary from which real perpendicular tangents just become possible.
4. Geometrical Meaning
- Any point on the director circle has exactly two real perpendicular tangents to the ellipse.
- If a point lies inside the director circle → perpendicular tangents not possible.
- If a point lies outside → two real tangents exist but not perpendicular.
5. Special Notes
- Director circle is widely used in locus, normal intersection, and reflection problems in JEE.
- It is symmetric about both coordinate axes for ellipse centered at origin.
Example
Find the equation of the director circle of the ellipse \( \dfrac{x^2}{25}+\dfrac{y^2}{9}=1. \)
▶️ Answer / Explanation
Here \( a=5,\ b=3 \).
Director circle:
\( x^2 + y^2 = a^2 + b^2 = 25 + 9 = 34 \)
Answer: \( x^2 + y^2 = 34 \)
Example
Check whether the point \( (7,1) \) lies inside, on or outside the director circle of \( \dfrac{x^2}{16}+\dfrac{y^2}{4}=1. \)
▶️ Answer / Explanation
\( a=4,\ b=2 \)
Director circle:
\( x^2 + y^2 = 20 \)
Compute:
\( 7^2 + 1^2 = 49 + 1 = 50 \)
Since 50 > 20 → point lies outside the director circle.
Answer: Outside (no perpendicular tangents possible)
Example
From point \( P(6,8) \), can two perpendicular tangents be drawn to the ellipse \( \dfrac{x^2}{9}+\dfrac{y^2}{4}=1? \)
▶️ Answer / Explanation
Ellipse parameters: \( a=3,\ b=2 \)
Director circle:
\( x^2 + y^2 = 9 + 4 = 13 \)
Check if point lies on or outside director circle:
\( 6^2 + 8^2 = 36 + 64 = 100 \)
100 > 13 → point lies outside.
Thus perpendicular tangents DO exist.
Ellipse: Chord of Contact
If two tangents are drawn from an external point \( P(x_1,y_1) \) to the ellipse, the line joining their points of contact is called the chord of contact.
Standard ellipse:
\( \dfrac{x^2}{a^2}+\dfrac{y^2}{b^2}=1 \)
1. Equation of Chord of Contact
For ellipse \( \dfrac{x^2}{a^2}+\dfrac{y^2}{b^2}=1, \) the chord of contact from point \( (x_1,y_1) \) is found by writing the tangent in point form and replacing: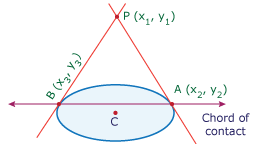
- \( x \to \dfrac{x+x_1}{2} \)
- \( y \to \dfrac{y+y_1}{2} \)
This gives the elegant formula:
\( \dfrac{x x_1}{a^2} + \dfrac{y y_1}{b^2} = 1 \)
This is exactly the same as tangent form but with \((x_1,y_1)\) as the external point.
This is the MOST important JEE formula for chord of contact of ellipse.
2. When Does Chord of Contact Exist?
Tangents must exist → point must lie outside the ellipse.
Condition:
\( \dfrac{x_1^2}{a^2} + \dfrac{y_1^2}{b^2} > 1 \)
3. Chord of Contact for Vertical Ellipse
Ellipse:
\( \dfrac{x^2}{b^2}+\dfrac{y^2}{a^2}=1 \)
Chord of contact from point \( (x_1,y_1) \):
\( \dfrac{x x_1}{b^2} + \dfrac{y y_1}{a^2} = 1 \)
4. Geometric Meaning
- The two tangents touch the ellipse at points \( T_1 \) and \( T_2 \).
- The line joining \( T_1 \) and \( T_2 \) is chord of contact.
- It represents the polar of point \( (x_1,y_1) \) with respect to ellipse.
5. Relation to Polar and Pole
- The chord of contact is the polar of point P.
- The external point P is the pole of that chord.
- Very important for conics theory problems.
Example
Find the chord of contact from point \( (6,4) \) to ellipse \( \dfrac{x^2}{25}+\dfrac{y^2}{9}=1. \)
▶️ Answer / Explanation
Chord of contact:
\( \dfrac{x x_1}{a^2} + \dfrac{y y_1}{b^2} = 1 \)
Here \( x_1=6,\ y_1=4,\ a^2=25,\ b^2=9 \).
\( \dfrac{6x}{25} + \dfrac{4y}{9} = 1 \)
Answer: \( \dfrac{6x}{25} + \dfrac{4y}{9} = 1 \)
Example
Find the chord of contact from point \( (3,-5) \) to ellipse \( \dfrac{x^2}{16}+\dfrac{y^2}{4}=1. \)
▶️ Answer / Explanation
Chord of contact:
\( \dfrac{3x}{16} + \dfrac{-5y}{4} = 1 \)
Simplify:
\( \dfrac{3x}{16} – \dfrac{5y}{4} = 1 \)
Answer: \( \dfrac{3x}{16} – \dfrac{5y}{4} = 1 \)
Example
Determine whether the point \( (2,1) \) can have a chord of contact with the ellipse \( \dfrac{x^2}{9}+\dfrac{y^2}{4}=1. \)
▶️ Answer / Explanation
Check if point lies outside ellipse:
\( \dfrac{2^2}{9} + \dfrac{1^2}{4} = \dfrac{4}{9} + \dfrac{1}{4} \)
\( = \dfrac{16 + 9}{36} = \dfrac{25}{36} \)
Since \( \dfrac{25}{36} < 1 \), point is inside ellipse.
Therefore, tangents cannot be drawn.
No chord of contact exists.
Ellipse: Pair of Tangents
If from a point \( P(x_1,y_1) \) two tangents can be drawn to the ellipse, the combined equation of those two tangents is called the pair of tangents from that point.
Ellipse:
\( \dfrac{x^2}{a^2}+\dfrac{y^2}{b^2}=1 \)
1. Combined Equation of Pair of Tangents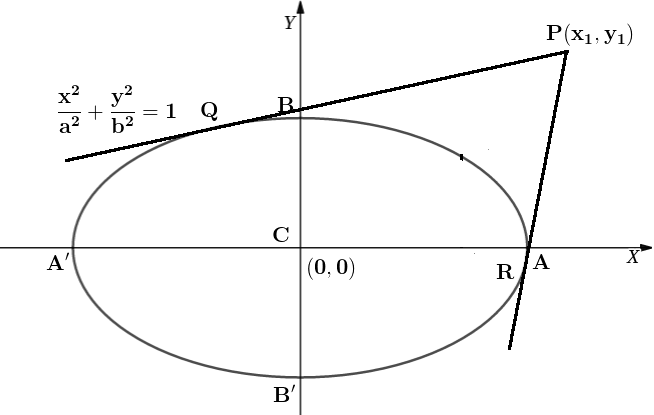
If \( P(x_1,y_1) \) lies outside the ellipse, i.e.,
\( \dfrac{x_1^2}{a^2} + \dfrac{y_1^2}{b^2} > 1, \)
then the equation of the pair of tangents from P is:
\( T^2 = SS_1 \)
2. Meaning of T, S, S₁
S: Original conic
\( S = \dfrac{x^2}{a^2} + \dfrac{y^2}{b^2} – 1 \)
T: Tangent in point form (replace \( x^2 \to xx_1,\ y^2 \to yy_1 \))
\( T = \dfrac{xx_1}{a^2} + \dfrac{yy_1}{b^2} – 1 \)
S₁: Value of S at the point \( (x_1,y_1) \)
\( S_1 = \dfrac{x_1^2}{a^2} + \dfrac{y_1^2}{b^2} – 1 \)
Formula:
\( \left(\dfrac{xx_1}{a^2} + \dfrac{yy_1}{b^2} – 1\right)^2 = \left(\dfrac{x^2}{a^2} + \dfrac{y^2}{b^2} – 1\right)\left(\dfrac{x_1^2}{a^2} + \dfrac{y_1^2}{b^2} – 1\right) \)
3. Condition for Tangents to Be Real
Real tangents exist only if:
\( S_1 > 0 \Rightarrow \dfrac{x_1^2}{a^2} + \dfrac{y_1^2}{b^2} > 1 \)
If \( S_1 = 0 \), point lies ON ellipse → both tangents coincide. If \( S_1 < 0 \), point lies INSIDE ellipse → no tangents exist.
4. Special Case
If point P lies on the director circle \( x^2 + y^2 = a^2 + b^2 \), then the two tangents are perpendicular.
5. Connection with Chord of Contact
- Pair of tangents meet ellipse at points T₁, T₂.
- Chord of contact = line joining T₁ and T₂.
- Equation is obtained by homogenising ellipse with chord of contact.
Example
Write the combined equation of pair of tangents from point \( (6,0) \) to the ellipse \( \dfrac{x^2}{25}+\dfrac{y^2}{9}=1. \)
▶️ Answer / Explanation
Here \( x_1 = 6,\ y_1 = 0 \).
\( T = \dfrac{6x}{25} – 1 \)
\( S = \dfrac{x^2}{25} + \dfrac{y^2}{9} – 1 \)
\( S_1 = \dfrac{36}{25} – 1 = \dfrac{11}{25} \)
Pair of tangents:
\( \left(\dfrac{6x}{25}-1\right)^2 = \left(\dfrac{x^2}{25} + \dfrac{y^2}{9} – 1\right)\left(\dfrac{11}{25}\right) \)
Answer: \( \left(\dfrac{6x}{25}-1\right)^2 = \dfrac{11}{25}\left(\dfrac{x^2}{25} + \dfrac{y^2}{9} – 1\right) \)
Example
Determine whether two tangents from point \( (2,3) \) to ellipse \( \dfrac{x^2}{16}+\dfrac{y^2}{9}=1 \) are real or imaginary.
▶️ Answer / Explanation
Check:
\( S_1 = \dfrac{4}{16} + \dfrac{9}{9} – 1 = \dfrac{1}{4} + 1 – 1 = \dfrac{1}{4} \)
Since \( S_1 > 0 \), tangents are real.
Answer: Real pair of tangents exists.
Example
For the ellipse \( \dfrac{x^2}{9}+\dfrac{y^2}{4}=1, \) find the locus of points from which two tangents drawn to the ellipse are perpendicular.
▶️ Answer / Explanation
Two tangents are perpendicular iff point lies on director circle.
Director circle for ellipse:
\( x^2 + y^2 = a^2 + b^2 \)
Here \( a=3,\ b=2 \):
\( x^2 + y^2 = 9 + 4 = 13 \)
Answer: Locus is the circle \( x^2 + y^2 = 13 \)
