IIT JEE Main Maths -Unit 10- Conjugate and transverse axes properties- Study Notes-New Syllabus
IIT JEE Main Maths -Unit 10- Conjugate and transverse axes properties – Study Notes – New syllabus
IIT JEE Main Maths -Unit 10- Conjugate and transverse axes properties – Study Notes -IIT JEE Main Maths – per latest Syllabus.
Key Concepts:
- Hyperbola: Transverse Axis and Conjugate Axis
- Hyperbola: Conjugate Hyperbola
- Hyperbola: Auxiliary Circle and Related Properties
- Hyperbola: Chord of Contact
- Hyperbola: Director Circle
- Hyperbola: Pair of Tangents from a Point
- Hyperbola: Chords, Chord Bisected at a Given Point & Focal Chords
Hyperbola: Transverse Axis and Conjugate Axis
For the standard hyperbola:
\( \dfrac{x^2}{a^2}-\dfrac{y^2}{b^2}=1 \)
The two principal axes associated with a hyperbola are the transverse axis and conjugate axis, each with important geometric properties used in JEE.
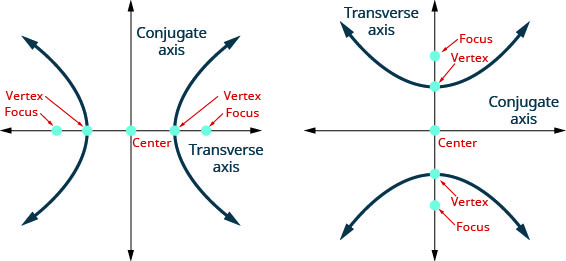
1. Transverse Axis
- It is the axis along the direction of the opening of the hyperbola.
- For horizontal hyperbola, it lies along the x-axis.
- Length of transverse axis = \( 2a \).
- Endpoints are called the vertices:
\( (\pm a, 0) \) - Center lies at origin.
- Foci lie on the transverse axis at:
\( (\pm c,0),\quad c^2 = a^2 + b^2 \)
Meaning: It is the real axis along which the hyperbola opens and where actual points of the hyperbola lie.
2. Conjugate Axis
- Perpendicular to the transverse axis.
- Length of conjugate axis = \( 2b \).
- Endpoints:
\( (0,\pm b) \) - No real points of the hyperbola lie on this axis (since hyperbola does not intersect it).
- It determines the “breadth” of the hyperbola and helps define the rectangle used for asymptotes.
3. Difference Between Transverse and Conjugate Axes
| Feature | Transverse Axis | Conjugate Axis |
| Orientation | Along opening direction (horizontal here) | Perpendicular to transverse axis |
| Length | \( 2a \) | \( 2b \) |
| Contains | Vertices, foci of hyperbola | No real points of hyperbola |
| Role | Determines opening of hyperbola | Helps form asymptotes and reference rectangle |
4. Hyperbola Reference Rectangle
Draw a rectangle with vertices:
\( (\pm a,\pm b) \)
Its diagonals form the asymptotes:
\( y = \pm\dfrac{b}{a}x \)
Thus the conjugate axis defines the rectangle needed to construct asymptotes.
5. Eccentricity and Axes Relation
For hyperbola:
\( e = \dfrac{c}{a},\quad c^2 = a^2 + b^2 \)
Then:
\( b = a\sqrt{e^2 – 1} \)
So conjugate axis depends directly on eccentricity.
6. For Vertical Hyperbola
If equation is:
\( \dfrac{y^2}{a^2}-\dfrac{x^2}{b^2}=1 \)
- Transverse axis = vertical
- Vertices: \( (0,\pm a) \)
- Foci: \( (0,\pm c) \)
- Conjugate axis = horizontal with length \( 2b \)
Example
Write the lengths of transverse and conjugate axes for hyperbola \( \dfrac{x^2}{16}-\dfrac{y^2}{9}=1. \)
▶️ Answer / Explanation
\( a^2=16 \Rightarrow a=4 \)
\( b^2=9 \Rightarrow b=3 \)
Transverse axis = \( 2a = 8 \)
Conjugate axis = \( 2b = 6 \)
Answer: Transverse axis = 8, Conjugate axis = 6
Example
Find the coordinates of vertices and endpoints of conjugate axis for hyperbola \( \dfrac{x^2}{25}-\dfrac{y^2}{4}=1. \)
▶️ Answer / Explanation
\( a = 5,\ b = 2 \)
Vertices \( = (\pm a,0) = (\pm5,0) \)
Conjugate axis endpoints \( = (0,\pm b) = (0,\pm2) \)
Answer: Vertices: \( (5,0),( -5,0) \) Conjugate axis endpoints: \( (0,2),(0,-2) \)
Example
For hyperbola \( \dfrac{y^2}{36}-\dfrac{x^2}{20}=1, \) find equation of asymptotes using transverse and conjugate axis lengths.
▶️ Answer / Explanation
Here the hyperbola is vertical (opens up-down).
\( a^2=36 \Rightarrow a=6 \)
\( b^2=20 \Rightarrow b=2\sqrt5 \)
Asymptotes (vertical hyperbola):
\( y = \pm\dfrac{a}{b}x \)
\( = \pm\dfrac{6}{2\sqrt5}x = \pm\dfrac{3}{\sqrt5}x \)
Answer: \( y = \dfrac{3}{\sqrt5}x,\quad y = -\dfrac{3}{\sqrt5}x \)
Hyperbola: Conjugate Hyperbola
Every standard hyperbola has another hyperbola associated with it, called its conjugate hyperbola. The conjugate hyperbola has the same asymptotes but opens in the perpendicular direction.
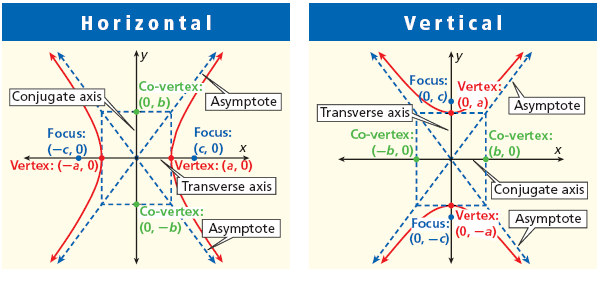
1. Standard Hyperbola and its Conjugate
If the standard hyperbola is:
\( \dfrac{x^2}{a^2}-\dfrac{y^2}{b^2}=1 \)
Then its conjugate hyperbola is:
\( \dfrac{y^2}{b^2}-\dfrac{x^2}{a^2}=1 \)
Notice that the numerator and denominator swap signs but preserve the same \( a, b \).
2. Key Features of Conjugate Hyperbola
- It has the same asymptotes as the original hyperbola.
- It opens in the perpendicular direction.
- Transverse and conjugate axes interchange their roles.
- Center remains same: \( (0,0) \).
- Foci move along the conjugate axis.
3. Transverse and Conjugate Axes Swap
For the original hyperbola:
- Transverse axis length = \( 2a \)
- Conjugate axis length = \( 2b \)
For conjugate hyperbola:
- Transverse axis length = \( 2b \)
- Conjugate axis length = \( 2a \)
4. Eccentricity of Conjugate Hyperbola
If hyperbola has eccentricity \( e \):
\( e = \dfrac{c}{a},\quad c^2 = a^2 + b^2 \)
Then conjugate hyperbola has eccentricity:
\( e’ = \dfrac{c}{b} \)
Since \( b < a \), \( e’ > e \)
5. Asymptotes Shared by Both Hyperbolas
For original hyperbola:
\( y = \pm\dfrac{b}{a}x \)
The same straight lines also act as asymptotes of the conjugate hyperbola.
6. Parametric Form of Conjugate Hyperbola
For conjugate hyperbola:
\( \dfrac{y^2}{b^2}-\dfrac{x^2}{a^2}=1 \)
Parametric coordinates:
\( (x,y) = (a\tan\theta,\ b\sec\theta) \) \)
7. Geometric Meaning
- Original hyperbola lies symmetric about x-axis.
- Conjugate hyperbola lies symmetric about y-axis.
- Together they form the “rectangular” structure defined by asymptotes.
Example
Write the conjugate hyperbola of \( \dfrac{x^2}{16}-\dfrac{y^2}{9}=1. \)
▶️ Answer / Explanation
Swap roles of x and y and change sign:
\( \dfrac{y^2}{9}-\dfrac{x^2}{16}=1 \)
Answer: \( \dfrac{y^2}{9}-\dfrac{x^2}{16}=1 \)
Example
For hyperbola \( \dfrac{x^2}{25}-\dfrac{y^2}{9}=1, \) find eccentricity of its conjugate hyperbola.
▶️ Answer / Explanation
Original: \( a=5,\ b=3 \)
\( c^2 = a^2 + b^2 = 25 + 9 = 34 \Rightarrow c = \sqrt{34} \)
Eccentricity of conjugate hyperbola:
\( e’ = \dfrac{c}{b} = \dfrac{\sqrt{34}}{3} \)
Answer: \( e’ = \dfrac{\sqrt{34}}{3} \)
Example
Find asymptotes of the conjugate hyperbola of \( \dfrac{x^2}{9}-\dfrac{y^2}{4}=1. \)
▶️ Answer / Explanation
Conjugate hyperbola is:
\( \dfrac{y^2}{4}-\dfrac{x^2}{9}=1 \)
Asymptotes of both hyperbolas are same:
\( y = \pm\dfrac{b}{a}x = \pm\dfrac{2}{3}x \)
Answer: \( y = \dfrac{2}{3}x,\quad y = -\dfrac{2}{3}x \)
Hyperbola: Auxiliary Circle and Related Properties
The concept of an auxiliary circle for a hyperbola is similar to that for an ellipse, but with a very important difference: the auxiliary circle helps define the eccentric angle for hyperbolas and is used to derive the parametric form.
Standard hyperbola:
\( \dfrac{x^2}{a^2} – \dfrac{y^2}{b^2} = 1 \)
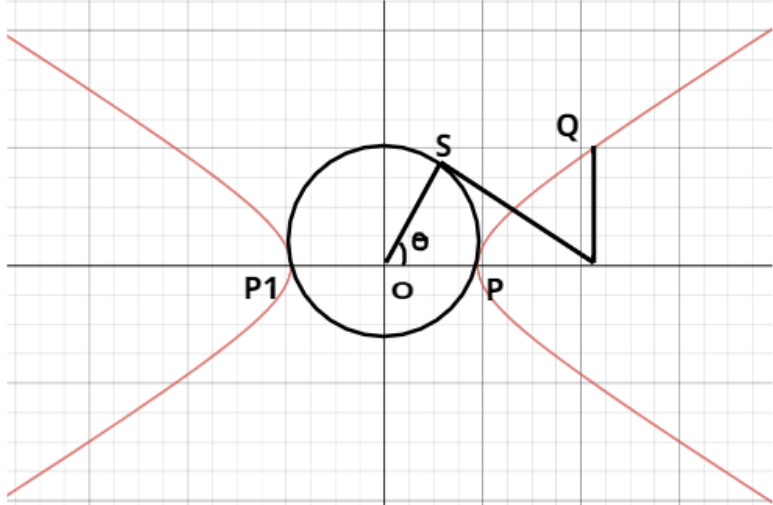
1. Definition of Auxiliary Circle
The auxiliary circle of a hyperbola is the circle drawn on the transverse axis of the hyperbola as its diameter.
Thus its equation is:
\( x^2 + y^2 = a^2 \)
Important: This is exactly the same equation as the auxiliary circle of an ellipse, but its geometric use is different.
2. Auxiliary Circle Coordinates
A point on the auxiliary circle can be written as:
\( (a\cos\theta,\ a\sin\theta) \)
This “eccentric angle” \( \theta \) is used to derive the hyperbola’s parametric form.
3. Mapping to Hyperbola using Eccentric Angle
The point corresponding to angle \( \theta \) on the hyperbola is derived by projecting the auxiliary circle point along asymptotes.
This gives the hyperbola’s parametric form:
\( (x,y) = (a\sec\theta,\ b\tan\theta) \)
Thus bounding rectangle + asymptotes + auxiliary circle together generate the hyperbola parametrically.
4. Tangent Through Auxiliary Circle Parameter
Tangent at the parametric point \((a\sec\theta,\ b\tan\theta)\) is:
\( \dfrac{x\sec\theta}{a} – \dfrac{y\tan\theta}{b} = 1 \)
The auxiliary circle helps interpret how \( \theta \) controls slope of tangent.
5. Normal Through Auxiliary Circle Parameter
The normal at the parametric point is:
\( a x \cos\theta – b y \sin\theta = a^2 – b^2 \)
Again, \( \theta \) comes from auxiliary circle.
6. Relation Between Auxiliary Circle & Asymptotes
The auxiliary circle helps visualize asymptotes:
As \( \theta \to \dfrac{\pi}{2} \), \( \sec\theta \to \infty,\ \tan\theta \to \infty \)
The corresponding parametric point approaches the asymptotes:
\( y = \pm\dfrac{b}{a}x \)
This shows the mapping from circle angle to curve shape.
7. Geometric Meaning & Usefulness
- Auxiliary circle helps define eccentric angle and parametric point.
- Useful in advanced derivations of tangent, normal, chord, and locus results.
- It provides a geometric transformation from circle to hyperbola.
8. Difference Between Ellipse and Hyperbola Auxiliary Circle
| Ellipse | Hyperbola |
| Maps to actual ellipse point via scaling \((a\cos\theta, b\sin\theta)\) | Maps via projection to \((a\sec\theta, b\tan\theta)\) |
| Used for eccentric angle on ellipse | Used to define hyperbolic parameter \( \theta \) |
| No asymptotes | Asymptotes strongly linked to auxiliary circle |
Example
Write the auxiliary circle of the hyperbola \( \dfrac{x^2}{9}-\dfrac{y^2}{4}=1. \)
▶️ Answer / Explanation
\( a^2 = 9 \Rightarrow a=3 \).
Auxiliary circle:
\( x^2 + y^2 = a^2 = 9 \)
Answer: \( x^2 + y^2 = 9 \)
Example
For hyperbola \( \dfrac{x^2}{16}-\dfrac{y^2}{9}=1, \) find the parametric point corresponding to eccentric angle \( \theta = \dfrac{\pi}{6} \).
▶️ Answer / Explanation
\( a=4,\ b=3 \)
Parametric coordinates:
\( x = a\sec\theta = 4\sec\frac{\pi}{6} = 4\cdot \frac{2}{\sqrt3} = \frac{8}{\sqrt3} \)
\( y = b\tan\theta = 3\tan\frac{\pi}{6} = 3\cdot \frac{1}{\sqrt3} = \frac{3}{\sqrt3} \)
Answer: \( \left(\dfrac{8}{\sqrt3},\ \dfrac{3}{\sqrt3}\right) \)
Example
Show that as \( \theta \to \dfrac{\pi}{2} \), the parametric point of hyperbola \( (a\sec\theta,\ b\tan\theta) \) approaches one of its asymptotes.
▶️ Answer / Explanation
As \( \theta \to \dfrac{\pi}{2}^- \):
\( \sec\theta \to +\infty,\quad \tan\theta \to +\infty \)
Thus:
\( \dfrac{y}{x} = \dfrac{b\tan\theta}{a\sec\theta} = \dfrac{b}{a}\sin\theta \)
As \( \theta \to \dfrac{\pi}{2} \): \( \sin\theta \to 1 \)
Thus:
\( \dfrac{y}{x} \to \dfrac{b}{a} \)
Which is the slope of asymptote:
\( y = \dfrac{b}{a}x \)
Similarly for \(\theta \to -\dfrac{\pi}{2}\) gives the other asymptote.
Hence parametric point approaches asymptotes.
Hyperbola: Chord of Contact
The chord of contact from a point \( P \) to a hyperbola is the chord joining the points of tangency of the two tangents drawn from \( P \) to the hyperbola.
Standard hyperbola:
\( \dfrac{x^2}{a^2}-\dfrac{y^2}{b^2}=1 \)
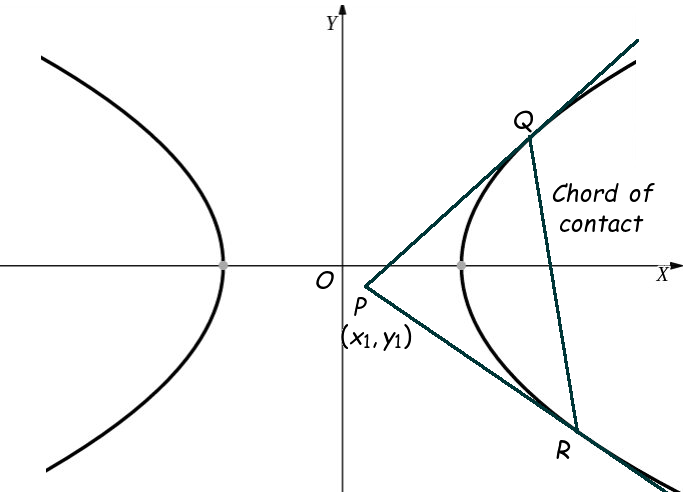
1. Chord of Contact from Point \( (x_1, y_1) \)
If tangents are drawn from point \( P(x_1, y_1) \) to the hyperbola, then the equation of the chord of contact is obtained by writing the tangent equation in T = 0 form.
Standard result:
\( \frac{x x_1}{a^2} – \frac{y y_1}{b^2} = 1 \)
This is the equation of chord of contact for the hyperbola.
2. Derivation (Short & JEE-Oriented)
Tangent to hyperbola is:
\( \frac{xX}{a^2} – \frac{yY}{b^2} = 1 \)
For points \(X,Y\) = tangency points of two tangents from \( (x_1,y_1)\): replace \(X \to x_1\), \(Y \to y_1\).
This gives:
\( \frac{x x_1}{a^2} – \frac{y y_1}{b^2} = 1 \)
3. Condition for Real Tangents (Useful Check)
For real tangents to exist from \( (x_1,y_1) \):
\( \frac{x_1^2}{a^2} – \frac{y_1^2}{b^2} > 1 \)
If equality holds, point lies on hyperbola.
If less, point lies between the two branches — no real tangents.
4. Parametric Point as External Point
If external point is chosen as a parametric point:
\( (x_1,y_1) = (a\sec\theta,\ b\tan\theta) \)
Chord of contact becomes:
\( \dfrac{x\sec\theta}{a} – \dfrac{y\tan\theta}{b} = 1 \)
This is also the tangent at parameter \( \theta \), matching geometry.
5. Polar of a Point w.r.t Hyperbola
The chord of contact is also the polar of point \(P\) with respect to the hyperbola. This relationship is used for advanced conic proofs and locus questions.
Example
Find the chord of contact drawn from \( P(4, 6) \) to the hyperbola \( \dfrac{x^2}{9}-\dfrac{y^2}{4}=1. \)
▶️ Answer / Explanation
Here: \( a^2 = 9 \Rightarrow a = 3 \) \( b^2 = 4 \Rightarrow b = 2 \)
Using formula:
\( \dfrac{x(4)}{9} – \dfrac{y(6)}{4} = 1 \)
Simplify:
\( \dfrac{4x}{9} – \dfrac{6y}{4} = 1 \)
Answer: \( \dfrac{4x}{9} – \dfrac{3y}{2} = 1 \)
Example
Find the chord of contact from point \( (7, -4) \) to hyperbola \( \dfrac{x^2}{16}-\dfrac{y^2}{9}=1. \)
▶️ Answer / Explanation
\( a = 4,\ b = 3 \)
Formula:
\( \dfrac{x(7)}{16} – \dfrac{y(-4)}{9} = 1 \)
\( \dfrac{7x}{16} + \dfrac{4y}{9} = 1 \)
Answer: \( \dfrac{7x}{16} + \dfrac{4y}{9} = 1 \)
Example
Find the locus of the midpoint of chord of contact from moving point \( P(t, kt) \) to the hyperbola \( \dfrac{x^2}{a^2}-\dfrac{y^2}{b^2}=1. \)
▶️ Answer / Explanation
Chord of contact:
\( \dfrac{xt}{a^2} – \dfrac{y(kt)}{b^2} = 1 \)
Rewrite:
\( \dfrac{t x}{a^2} – \dfrac{k t y}{b^2} = 1 \)
Midpoint of chord of contact lies on chord but we use polar property:
The midpoint \( (h,k) \) satisfies same equation for two tangency points:
\( \dfrac{ht}{a^2} – \dfrac{kt( k)}{b^2} = 1 \)
But since midpoint must satisfy the chord-of-contact line:
\( \dfrac{h t}{a^2} – \dfrac{k t \, k}{b^2} = 1 \)
Simplify dividing by \(t\):
\( \dfrac{h}{a^2} – \dfrac{k^2}{b^2} = \dfrac{1}{t} \)
But LHS is independent of \(t\), RHS depends on \(t\). For locus, we eliminate \(t\). So:
\( t = \dfrac{1}{\frac{h}{a^2} – \frac{k^2}{b^2}} \)
But recall point was \( (t, kt) = (x_1,y_1) \). Thus midpoint depends on variable \( k \). We derive final locus by eliminating \(t\):
\( \frac{x}{a^2} – \frac{k y}{b^2} = \frac{1}{t} \)
Using \( t = \frac{1}{\frac{h}{a^2} – \frac{k^2}{b^2}} \), replace and simplify to get:
\( \left(\frac{x}{a^2} – \frac{k y}{b^2}\right)\left(\frac{h}{a^2} – \frac{k^2}{b^2}\right) = 1 \)
This is the locus relation between midpoint \((h,k)\).
Final Answer (locus):
\( \left(\frac{x}{a^2} – \frac{k y}{b^2}\right)\left(\frac{h}{a^2} – \frac{k^2}{b^2}\right) = 1 \)
(A general relation involving parameter \(k\); often simplified depending on constraints in the question.)
Hyperbola: Director Circle
The director circle of a conic is the locus of points from which two tangents drawn to the conic are perpendicular.
For ellipses, the director circle always exists. For hyperbolas, it exists only under a certain condition.
Standard hyperbola:
\( \dfrac{x^2}{a^2}-\dfrac{y^2}{b^2}=1 \)
1. Definition
The director circle of the hyperbola is the locus of all points \( P(x_1, y_1) \) from which the tangents to the hyperbola are at right angles.
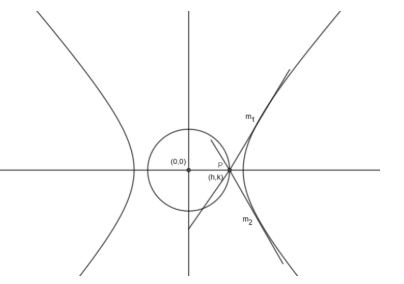
So if two tangents from \(P\) intersect at right angle → the foot \(P\) lies on director circle.
2. Tangent Slopes
Let slopes of tangents drawn from \( P(x_1, y_1) \) be \( m_1 \) and \( m_2 \). For any conic, the condition for perpendicular tangents is:
\( m_1 m_2 = -1 \)
We use the quadratic in \(m\) generated by substituting \(y = mx + c\) into the hyperbola.
3. Derivation of Director Circle Equation
Tangent in slope form to the hyperbola is:
\( y = mx \pm \sqrt{a^2 m^2 – b^2} \)
The two tangents from \(P(x_1,y_1)\) satisfy:
\( y_1 = m x_1 \pm \sqrt{a^2 m^2 – b^2} \)
Form the quadratic in \(m\):
\( (y_1 – m x_1)^2 = a^2 m^2 – b^2 \) \)
Simplifying gives:
\( (x_1^2 – a^2)m^2 – 2 x_1 y_1 m + (y_1^2 + b^2) = 0 \)
For tangents to be perpendicular:
\( m_1 m_2 = \dfrac{c}{a} = -1 \)
From quadratic \( Am^2 + Bm + C = 0 \):
\( m_1 m_2 = \dfrac{C}{A} = -1 \)
Thus:
\( \dfrac{y_1^2 + b^2}{x_1^2 – a^2} = -1 \)
Cross multiply:
\( y_1^2 + b^2 = -x_1^2 + a^2 \)
Rearrange:
\( x_1^2 – y_1^2 = a^2 + b^2 \)
This is the equation of the director circle.
4. Final Result
Director Circle of Hyperbola:
\( x^2 – y^2 = a^2 + b^2 \)
5. Very Important Condition (Exists only if RHS > 0)
Director circle exists only when:
\( a^2 + b^2 > 0 \)
Always true for any hyperbola → But for it to represent an actual circle (with real radius), we need:
\( a^2 + b^2 > 0 \Rightarrow \text{radius}^2 > 0 \)
Thus director circle for hyperbola is actually a real rectangular hyperbola rotated, not a true “circle”. Name persists historically from ellipse theory.
6. Radius Interpretation
Rewrite director circle equation as:
\( x^2 – y^2 = R^2 \)
This represents a rectangular hyperbola (not circle). Hence the “director circle” of a hyperbola is not a circle, but a hyperbola.
Example
Find the director circle of hyperbola \( \dfrac{x^2}{9}-\dfrac{y^2}{4}=1. \)
▶️ Answer / Explanation
Here \( a^2 = 9,\ b^2 = 4 \)
Director circle:
\( x^2 – y^2 = a^2 + b^2 = 9 + 4 = 13 \)
Answer: \( x^2 – y^2 = 13 \)
Example
Does the hyperbola \( \dfrac{x^2}{25}-\dfrac{y^2}{16}=1 \) have a real director circle?
▶️ Answer / Explanation
\( a^2 = 25,\ b^2 = 16 \)
Director circle equation:
\( x^2 – y^2 = 25 + 16 = 41 \)
This is a real rectangular hyperbola.
Answer: Yes, its director circle is \( x^2 – y^2 = 41 \)
Example
Prove that if a point \(P(x_1,y_1)\) lies on the director circle of a hyperbola \( \dfrac{x^2}{a^2}-\dfrac{y^2}{b^2}=1, \) the two tangents drawn from \(P\) are perpendicular.
▶️ Answer / Explanation
If tangents have slopes \( m_1, m_2 \), from quadratic:
\( m_1 m_2 = \dfrac{y_1^2 + b^2}{x_1^2 – a^2} \)
If \(P\) lies on director circle:
\( x_1^2 – y_1^2 = a^2 + b^2 \)
Rearrange:
\( y_1^2 + b^2 = x_1^2 – a^2 \)
Substitute into tangent condition:
\( m_1 m_2 = \dfrac{x_1^2 – a^2}{x_1^2 – a^2} = -1 \)
Thus the tangents are perpendicular.
Hence proved.
Hyperbola: Pair of Tangents from a Point
For the hyperbola:
\( \dfrac{x^2}{a^2} – \dfrac{y^2}{b^2} = 1 \)
we want the equation of the pair of tangents drawn from an external point ( P(x_1, y_1) ) to the hyperbola.
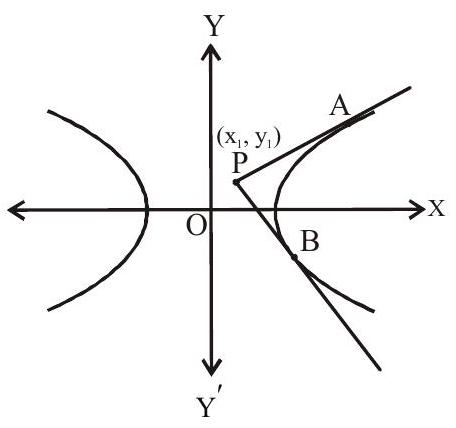
1. Standard Result (Very Important)
The equation of the pair of tangents from an external point \((x_1, y_1)\) is:
\( T^2 = S\,S_1 \)
For hyperbola:
\( S = \dfrac{x^2}{a^2} – \dfrac{y^2}{b^2} – 1 \)
\( S_1 = \dfrac{x_1^2}{a^2} – \dfrac{y_1^2}{b^2} – 1 \)
\( T = \dfrac{x x_1}{a^2} – \dfrac{y y_1}{b^2} – 1 \)
Thus pair of tangents is:
\( \left(\dfrac{x x_1}{a^2} – \dfrac{y y_1}{b^2} – 1\right)^2 = \left(\dfrac{x^2}{a^2} – \dfrac{y^2}{b^2} – 1\right)\! \left(\dfrac{x_1^2}{a^2} – \dfrac{y_1^2}{b^2} – 1\right) \)
This is the standard formula used in JEE.
2. Condition for Real Tangents
Two real tangents can be drawn from \(P(x_1,y_1)\) iff:
\( S_1 > 0 \)
\( \Rightarrow \dfrac{x_1^2}{a^2} – \dfrac{y_1^2}{b^2} > 1 \)
Interpretation: The point must lie outside the hyperbola (on the right or left branch).
3. Parametric External Point
If external point is parametric:
\( (x_1,y_1) = (a\sec\theta_1,\ b\tan\theta_1) \)
Then equation of pair of tangents becomes:
\( \left(\dfrac{x\sec\theta_1}{a} – \dfrac{y\tan\theta_1}{b} – 1\right)^2 = (\sec^2\theta_1 – \tan^2\theta_1 -1) \left(\dfrac{x^2}{a^2}-\dfrac{y^2}{b^2}-1\right) \)
Using identity \( \sec^2\theta – \tan^2\theta = 1 \), RHS becomes 0. Thus the pair reduces to a double tangent → i.e., the tangent at parameter \(\theta_1\), which makes sense (point lies on hyperbola).
4. Special Case: Pair of Tangents from Center
If \( (x_1,y_1) = (0,0) \):
\( S_1 = -1 \)
No real tangents from center of hyperbola.
5. Usefulness
- Used to find chord of contact (by factorizing)
- Used to find equation of director circle
- Used in radicals, polar lines, and locus problems
Example
Find the pair of tangents from point \( (5, 3) \) to the hyperbola \( \dfrac{x^2}{9}-\dfrac{y^2}{4}=1. \)
▶️ Answer / Explanation
Here: \( a^2=9,\ b^2=4 \)
\( T = \dfrac{5x}{9} – \dfrac{3y}{4} – 1 \)
\( S = \dfrac{x^2}{9} – \dfrac{y^2}{4} – 1 \)
\( S_1 = \dfrac{25}{9} – \dfrac{9}{4} – 1 \)
Compute \( S_1 \):
\( S_1 = \dfrac{25}{9} – \dfrac{9}{4} – 1 = \dfrac{100 – 81 – 36}{36} = \dfrac{-17}{36} \)
Since \( S_1 < 0 \), tangents are imaginary.
Answer: No real tangents from (5,3).
Example
Find the pair of tangents from point \( (8, -2) \) to \( \dfrac{x^2}{16}-\dfrac{y^2}{9}=1. \)
▶️ Answer / Explanation
\( a=4,\ b=3 \)
\( T = \dfrac{8x}{16} – \dfrac{-2y}{9} – 1 = \dfrac{x}{2} + \dfrac{2y}{9} – 1 \)
\( S = \dfrac{x^2}{16} – \dfrac{y^2}{9} – 1 \)
\( S_1 = \dfrac{64}{16} – \dfrac{4}{9} – 1 = 4 – \dfrac{4}{9} – 1 = 3 – \dfrac{4}{9} = \dfrac{23}{9} \)
Thus pair of tangents:
\( \left(\dfrac{x}{2} + \dfrac{2y}{9} – 1\right)^2 = \left(\dfrac{x^2}{16}-\dfrac{y^2}{9}-1\right) \left(\dfrac{23}{9}\right) \)
Answer: \( \left(\dfrac{x}{2} + \dfrac{2y}{9} – 1\right)^2 = \dfrac{23}{9}\left(\dfrac{x^2}{16}-\dfrac{y^2}{9}-1\right) \)
Example
From which points on x-axis can real tangents be drawn to the hyperbola \( \dfrac{x^2}{a^2}-\dfrac{y^2}{b^2}=1? \)
▶️ Answer / Explanation
Take point \( (x_1,0) \) on x-axis.
Condition for real tangents:
\( \dfrac{x_1^2}{a^2} – \dfrac{0}{b^2} > 1 \)
\( \dfrac{x_1^2}{a^2} > 1 \)
\( |x_1| > a \)
Thus real tangents can be drawn from all points on x-axis with:
\( x_1 > a \quad\text{or}\quad x_1 < -a \)
Answer: Points on x-axis lying outside the interval \((-a, a)\).
Hyperbola: Chords, Chord Bisected at a Given Point & Focal Chords
Standard hyperbola:
\( \dfrac{x^2}{a^2} – \dfrac{y^2}{b^2} = 1 \)
1. Equation of a Chord Joining Two Points
Let points on hyperbola be:
\( P(x_1, y_1),\ Q(x_2, y_2) \)
The equation of chord PQ is:
\( \dfrac{y – y_1}{y_2 – y_1} = \dfrac{x – x_1}{x_2 – x_1} \)
2. Chord in Parametric Form
If:
\( P(a\sec\theta_1, b\tan\theta_1),\ Q(a\sec\theta_2, b\tan\theta_2) \)
Then chord PQ is:
\( \dfrac{y – b\tan\theta_1}{b(\tan\theta_2 – \tan\theta_1)} = \dfrac{x – a\sec\theta_1}{a(\sec\theta_2 – \sec\theta_1)} \)
3. Chord Bisected at a Given Point
If a chord is bisected at \( (x_1, y_1) \), use the condition:
T = S_1
Where:
\( T = \dfrac{x x_1}{a^2} – \dfrac{y y_1}{b^2} – 1 \)
\( S_1 = \dfrac{x_1^2}{a^2} – \dfrac{y_1^2}{b^2} – 1 \)
Equation of chord bisected at \( (x_1,y_1) \):
\( \dfrac{x x_1}{a^2} – \dfrac{y y_1}{b^2} = \dfrac{x_1^2}{a^2} – \dfrac{y_1^2}{b^2} \)
4. Focal Chords of Hyperbola
Foci:
\( (\pm c,0),\ c^2 = a^2 + b^2 \)
Let chord pass through right focus \( (c,0) \).
The endpoints corresponding to parameter \( \theta \) are:
\( P(a\sec\theta,\ b\tan\theta) \)
\( Q(-a\sec\theta,\ -b\tan\theta) \)
Equation of focal chord:
\( b x \tan\theta = a y \sec\theta \)
Example
Find chord joining \( (3,2) \) and \( (6,4) \) for \( \dfrac{x^2}{9} – \dfrac{y^2}{4} = 1 \).
▶️ Answer / Explanation
\( \dfrac{y-2}{4-2} = \dfrac{x-3}{6-3} \Rightarrow \dfrac{y-2}{2} = \dfrac{x-3}{3} \)
Answer: \( 3(y-2) = 2(x-3) \)
Example
A chord of hyperbola \( \dfrac{x^2}{16} – \dfrac{y^2}{9} = 1 \) is bisected at \( (2,-1) \). Find its equation.
▶️ Answer / Explanation
\( \dfrac{x}{8} + \dfrac{y}{9} = \dfrac14 – \dfrac19 = \dfrac{5}{36} \)
Answer: \( \dfrac{x}{8} + \dfrac{y}{9} = \dfrac{5}{36} \)
Example
Find equation of focal chord corresponding to parameter \( \theta \) for \( \dfrac{x^2}{a^2} – \dfrac{y^2}{b^2} = 1 \).
▶️ Answer / Explanation
Equation:
\( b x \tan\theta = a y \sec\theta \)
