IIT JEE Main Maths -Unit 10- Equation of tangent, chord, and pair of tangents- Study Notes-New Syllabus
IIT JEE Main Maths -Unit 10- Equation of tangent, chord, and pair of tangents – Study Notes – New syllabus
IIT JEE Main Maths -Unit 10- Equation of tangent, chord, and pair of tangents – Study Notes -IIT JEE Main Maths – per latest Syllabus.
Key Concepts:
- Circle: Equation of Tangent, Chord, and Pair of Tangents
- Condition for Tangency + Length of Tangent
Circle: Equation of Tangent, Chord, and Pair of Tangents
For a circle \( S \equiv x^2 + y^2 + 2gx + 2fy + c = 0 \), the standard method used is the transformation:
Replace \( x^2 + y^2 + 2gx + 2fy + c \) by \( S \) and replace \( x^2 \) by \( xx_1 \), \( y^2 \) by \( yy_1 \), etc. This gives the tangent/chord/pair of tangents equation.
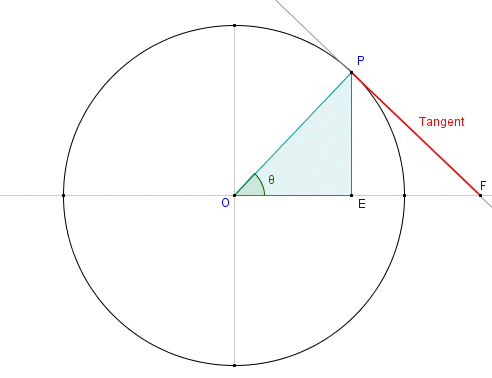
1. Equation of Tangent to a Circle
(A) Tangent at Point \( (x_1, y_1) \) on the Circle
If point \( (x_1, y_1) \) lies on the circle \( x^2 + y^2 + 2gx + 2fy + c = 0 \), then tangent is:
\( xx_1 + yy_1 + g(x + x_1) + f(y + y_1) + c = 0 \)
For circle centered at origin \( x^2+y^2=r^2 \):
\( xx_1 + yy_1 = r^2 \)
(B) Tangent in Slope Form
For circle \( x^2 + y^2 = r^2 \), tangent with slope \( m \):
\( y = mx \pm \sqrt{r^2(1 + m^2)} \)
(C) Condition for Tangency for Line \( y = mx + c \)
The line \( y = mx + c \) is tangent to \( x^2 + y^2 = r^2 \) if:
\( \dfrac{|c|}{\sqrt{1 + m^2}} = r \)
2. Equation of Chord Joining Two Points
If \( P(x_1, y_1) \) and \( Q(x_2, y_2) \) lie on the circle, the chord \( PQ \) equation is:
\( (x_1 – x_2)x + (y_1 – y_2)y = \dfrac{x_1^2 – x_2^2 + y_1^2 – y_2^2}{2} \)
3. Equation of Chord with Midpoint Given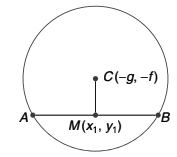
If midpoint of chord is \( M(h, k) \), equation of chord is:
\( T = S_1 \)
Where \( T = xx_1 + yy_1 + g(x + x_1) + f(y + y_1) + c \), using \( x_1 = h,\ y_1 = k \).
Thus, chord with midpoint \( (h,k) \):
\( xx_1 + yy_1 + g(x + x_1) + f(y + y_1) + c = 0 \)
4. Equation of Pair of Tangents from a Point
For circle \( S \equiv x^2 + y^2 + 2gx + 2fy + c = 0 \), pair of tangents from point \( (x_1, y_1) \) is given by:
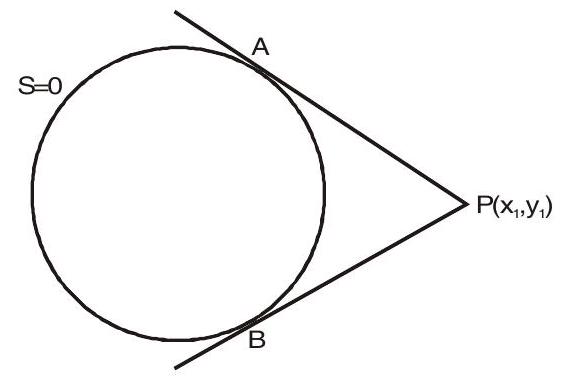
\( T^2 = SS_1 \)
Where
- \( T = xx_1 + yy_1 + g(x + x_1) + f(y + y_1) + c \)
- \( S_1 = x_1^2 + y_1^2 + 2gx_1 + 2fy_1 + c \)
This represents two tangents if \( S_1 > 0 \).
Special case (circle at origin):
For \( x^2 + y^2 = r^2 \), pair of tangents from \( (x_1, y_1) \):
\( (xx_1 + yy_1)^2 = (x_1^2 + y_1^2 – r^2)(x^2 + y^2) \)
Example
Find the tangent to the circle \( x^2 + y^2 = 25 \) at point \( (3,4) \).
▶️ Answer / Explanation
Use formula for circle centered at origin:
\( xx_1 + yy_1 = r^2 \)
\( 3x + 4y = 25 \)
Answer: \( 3x + 4y = 25 \)
Example
Find the equation of the chord of the circle \( x^2 + y^2 = 13 \) joining points \( (2, -3) \) and \( (3, 2) \).
▶️ Answer / Explanation
Use chord formula:
\( (x_1 – x_2)x + (y_1 – y_2)y = \dfrac{x_1^2 – x_2^2 + y_1^2 – y_2^2}{2} \)
Compute LHS:
\( (2 – 3)x + (-3 – 2)y = -x – 5y \)
RHS:
\( \dfrac{4 – 9 + 9 – 4}{2} = 0 \)
So equation is:
\( -x – 5y = 0 \)
Or \( x + 5y = 0 \)
Answer: \( x + 5y = 0 \)
Example
Find the equation of the pair of tangents drawn from point \( (4,6) \) to the circle \( x^2 + y^2 – 4x – 6y – 3 = 0 \).
▶️ Answer / Explanation
Step 1: Identify S and T
\( S = x^2 + y^2 – 4x – 6y – 3 \)
Point: \( (x_1, y_1) = (4, 6) \)
Step 2: Compute \( S_1 \)
\( S_1 = 4^2 + 6^2 – 4(4) – 6(6) – 3 \)
= \( 16 + 36 – 16 – 36 – 3 = -3 \)
Step 3: Write T
\( T = xx_1 + yy_1 – 2(x + x_1) – 3(y + y_1) – 3 \)
Substitute:
\( T = 4x + 6y – 4(x + 4) – 3(y + 6) – 3 \)
= \( 4x + 6y – 4x – 16 – 3y – 18 – 3 = 3y – 37 \)
Step 4: Apply formula
\( T^2 = SS_1 \)
\( (3y – 37)^2 = -3(x^2 + y^2 – 4x – 6y – 3) \)
This is the required pair of tangents.
Answer: \( (3y – 37)^2 = -3(x^2 + y^2 – 4x – 6y – 3) \)
Condition for Tangency + Length of Tangent
For a circle \( S \equiv x^2 + y^2 + 2gx + 2fy + c = 0 \), and a line \( L \equiv lx + my + n = 0 \), we want to know:
- When is the line tangent to the circle?
- What is the length of tangent from a point to the circle?
1. Condition for Tangency of a General Line to a General Circle
A line \( lx + my + n = 0 \) is tangent to circle \( x^2 + y^2 + 2gx + 2fy + c = 0 \) if perpendicular distance from center to line = radius.
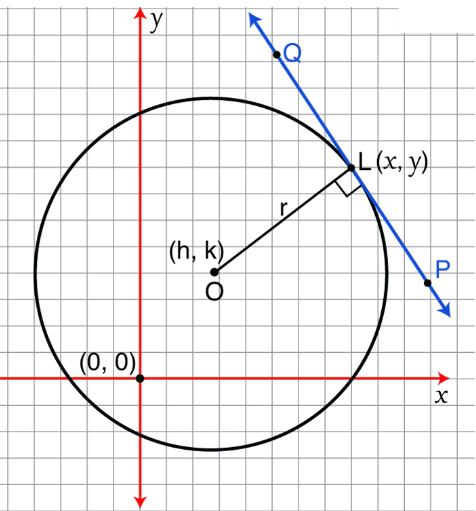
Center: \( (-g, -f) \)
Radius: \( r = \sqrt{g^2 + f^2 – c} \)
Distance from center to line:
\( d = \dfrac{| -gl – fm + n |}{\sqrt{l^2 + m^2}} \)
Condition for tangency:
\( d = r \)
Thus, the line is tangent to the circle iff:
\( \dfrac{| -gl – fm + n |}{\sqrt{l^2 + m^2}} = \sqrt{g^2 + f^2 – c} \)
Or squared form (JEE-friendly):
\( (-gl – fm + n)^2 = (g^2 + f^2 – c)(l^2 + m^2) \)
2. Condition of Tangency in Slope Form
For circle \( x^2 + y^2 = r^2 \) and line \( y = mx + c \):
Line is tangent ⟺ \( \dfrac{|c|}{\sqrt{1 + m^2}} = r \)
That is:
\( c^2 = r^2(1 + m^2) \)
3. Length of Tangent From a Point to a Circle
If point \( P(x_1, y_1) \) is outside the circle \( x^2 + y^2 + 2gx + 2fy + c = 0 \), then the length of tangent \( PT \) drawn from \( P \) is:
\( PT = \sqrt{S_1} \)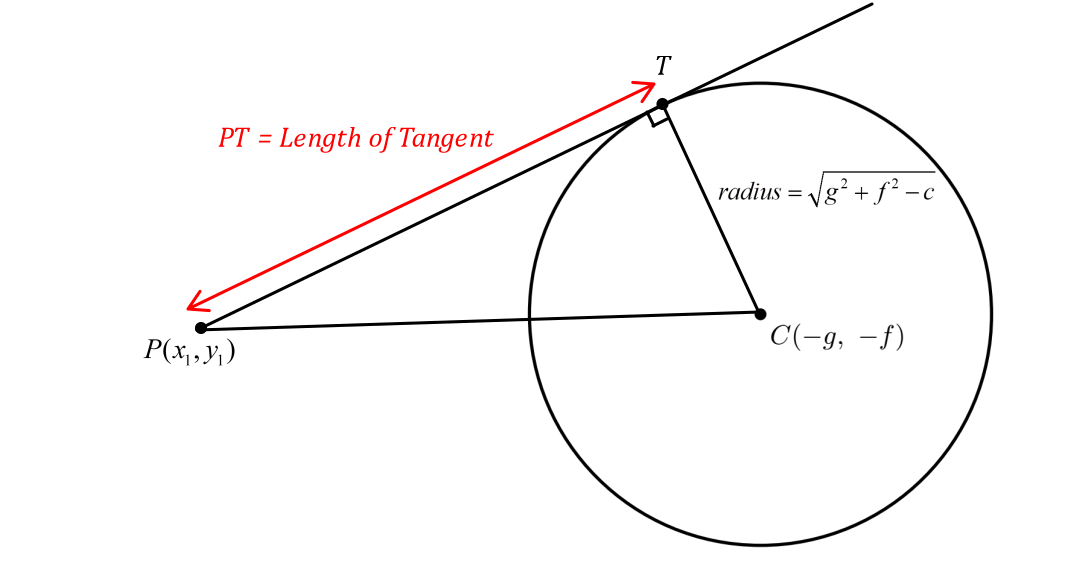
Where:
\( S_1 = x_1^2 + y_1^2 + 2gx_1 + 2fy_1 + c \)
Meaning:
- If \( S_1 > 0 \) → two tangents exist
- If \( S_1 = 0 \) → point lies on circle → 1 tangent (touching)
- If \( S_1 < 0 \) → no tangent possible
This result is used VERY frequently in JEE Main.
4. Relationship Between Both Concepts
If the line from point \( P(x_1, y_1) \) is tangent to circle, then:
Length of tangent squared = power of point \( S_1 \)
This helps in quickly checking tangency without distance formula.
Example
Find the condition that the line \( y = 2x + c \) is tangent to \( x^2 + y^2 = 25 \).
▶️ Answer / Explanation
Use slope-form condition:
\( \dfrac{|c|}{\sqrt{1 + 2^2}} = 5 \)
\( \dfrac{|c|}{\sqrt{5}} = 5 \)
\( |c| = 5\sqrt{5} \)
Answer: \( c = \pm 5\sqrt{5} \)
Example
Find the length of the tangent from point \( (6,8) \) to the circle \( x^2 + y^2 – 4x – 6y – 12 = 0 \).
▶️ Answer / Explanation
Step 1: Compute \( S_1 \)
\( S_1 = 6^2 + 8^2 – 4(6) – 6(8) – 12 \)
\( = 36 + 64 – 24 – 48 – 12 = 16 \)
Step 2: Length of tangent
\( PT = \sqrt{S_1} = 4 \)
Answer: 4
Example
Find the value of \( k \) such that the line \( 3x + 4y + k = 0 \) is tangent to the circle \( x^2 + y^2 – 2x + 4y – 20 = 0 \).
▶️ Answer / Explanation
Step 1: Identify center and radius
Center: \( (1, -2) \)
Radius: \( r = \sqrt{1^2 + (-2)^2 – (-20)} = \sqrt{1 + 4 + 20} = 5 \)
Step 2: Apply tangency condition
Distance from center to line = radius
\( \dfrac{|3(1) + 4(-2) + k|}{5} = 5 \)
\( |3 – 8 + k| = 25 \)
\( |k – 5| = 25 \)
Cases:
\( k – 5 = 25 \Rightarrow k = 30 \)
\( k – 5 = -25 \Rightarrow k = -20 \)
Answer: \( k = 30 \) or \( k = -20 \)
