IIT JEE Main Maths -Unit 10- Hyperbola : Tangent and normal equation- Study Notes-New Syllabus
IIT JEE Main Maths -Unit 10- Hyperbola : Tangent and normal equation – Study Notes – New syllabus
IIT JEE Main Maths -Unit 10- Hyperbola : Tangent and normal equation – Study Notes -IIT JEE Main Maths – per latest Syllabus.
Key Concepts:
Hyperbola: Equation of Tangent
Hyperbola: Equation of Normal
Hyperbola: Asymptotes
Hyperbola: Equation of Tangent
For the standard hyperbola:
\( \dfrac{x^2}{a^2} – \dfrac{y^2}{b^2} = 1 \)
The tangent can be written in three important forms:
(1) Point form, (2) Parametric form, (3) Slope form.
1. Tangent at a Point on Hyperbola (Point Form)
If \( (x_1, y_1) \) lies on the hyperbola, then the tangent is:
\( \dfrac{x x_1}{a^2} – \dfrac{y y_1}{b^2} = 1 \)
This is obtained by replacing:
- \(x^2 \to xx_1\)
- \(y^2 \to yy_1\)
2. Tangent in Parametric Form
Parametric point on hyperbola:
\( (x_1,y_1) = (a\sec\theta,\ b\tan\theta) \)
Substitute in point form to get:
\( \dfrac{x\sec\theta}{a} – \dfrac{y\tan\theta}{b} = 1 \)
This form is used extensively in JEE locus and tangent–normal questions.
3. Tangent in Slope Form
If tangent has slope \( m \), write line as \( y = mx + c \). For tangency, the equation must satisfy:
\( c = \pm\sqrt{a^2 m^2 – b^2} \)
Thus tangent in slope form is:
\( y = mx \pm\sqrt{a^2 m^2 – b^2} \)
Condition for real tangent:
\( a^2 m^2 – b^2 \ge 0 \Rightarrow |m| \ge \dfrac{b}{a} \)
This relates slope of tangent with asymptotes.
4. Condition of Tangency for General Line
Given line:
\( y = mx + c \)
It touches the hyperbola iff:
\( c^2 = a^2 m^2 – b^2 \)
This is one of the most important formulas for JEE MCQs.
5. Tangent to Vertical Hyperbola
For:
\( \dfrac{y^2}{a^2} – \dfrac{x^2}{b^2} = 1 \)
Tangent at \( (x_1,y_1) \):
\( \dfrac{y y_1}{a^2} – \dfrac{x x_1}{b^2} = 1 \)
Parametric form becomes:
\( \dfrac{y\sec\theta}{a} – \dfrac{x\tan\theta}{b} = 1 \)
6. Special Tangents
- At vertex \( (a,0) \): tangent is \( x = a \)
- At vertex \( (-a,0) \): tangent is \( x = -a \)
- Asymptotes behave like tangents at infinity
Example
Find the tangent to hyperbola \( \dfrac{x^2}{9}-\dfrac{y^2}{4}=1 \) at point \( (3,\ 2) \).
▶️ Answer / Explanation
Use point-form tangent:
\( \dfrac{x x_1}{a^2} – \dfrac{y y_1}{b^2} = 1 \)
Here \( a^2 = 9,\ b^2 = 4 \).
\( \dfrac{3x}{9} – \dfrac{2y}{4} = 1 \)
\( \dfrac{x}{3} – \dfrac{y}{2} = 1 \)
Answer: \( \dfrac{x}{3} – \dfrac{y}{2} = 1 \)
Example
Find tangent at parametric point \( \theta = \dfrac{\pi}{6} \) for hyperbola \( \dfrac{x^2}{25}-\dfrac{y^2}{16}=1. \)
▶️ Answer / Explanation
Parametric tangent:
\( \dfrac{x\sec\theta}{a} – \dfrac{y\tan\theta}{b} = 1 \)
Here \( a=5,\ b=4 \).
\( \sec\frac{\pi}{6} = \frac{2}{\sqrt{3}},\quad \tan\frac{\pi}{6} = \frac{1}{\sqrt{3}} \)
Substitute:
\( \dfrac{x \cdot \frac{2}{\sqrt{3}}}{5} – \dfrac{y \cdot \frac{1}{\sqrt{3}}}{4} = 1 \)
Simplify:
\( \dfrac{2x}{5\sqrt{3}} – \dfrac{y}{4\sqrt{3}} = 1 \)
Answer: \( \dfrac{2x}{5\sqrt{3}} – \dfrac{y}{4\sqrt{3}} = 1 \)
Example
Find the slope(s) of tangent(s) to hyperbola \( \dfrac{x^2}{16}-\dfrac{y^2}{9}=1 \) that pass through point \( (0,5) \).
▶️ Answer / Explanation
Assume tangent through (0,5) is: \( y – 5 = m(x – 0) \Rightarrow y = mx + 5 \)
Condition of tangency:
\( c^2 = a^2 m^2 – b^2 \)
Here \( c = 5,\ a=4,\ b=3 \).
\( 5^2 = 16 m^2 – 9 \)
\( 25 = 16 m^2 – 9 \)
\( 16 m^2 = 34 \Rightarrow m^2 = \dfrac{34}{16} = \dfrac{17}{8} \)
\( m = \pm\sqrt{\dfrac{17}{8}} \)
Answer: \( m = \pm\dfrac{\sqrt{17}}{2\sqrt{2}} \)
Hyperbola: Equation of Normal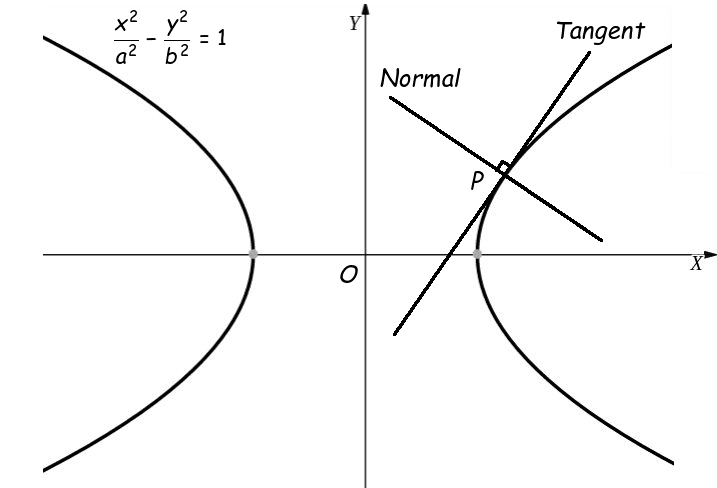
For the standard hyperbola:
\( \dfrac{x^2}{a^2}-\dfrac{y^2}{b^2}=1 \)
The normal is the line perpendicular to the tangent at the point of contact.
1. Normal at a Point on Hyperbola (Point Form)
If \( (x_1,y_1) \) lies on the hyperbola, slope of tangent is:
\( m_t = \dfrac{b^2 x_1}{a^2 y_1} \)
Thus slope of normal is negative reciprocal:
\( m_n = -\dfrac{a^2 y_1}{b^2 x_1} \)
Normal equation:
\( y – y_1 = -\dfrac{a^2 y_1}{b^2 x_1}(x – x_1) \)
2. Normal in Parametric Form (Most Important for JEE)
Parametric point on hyperbola:
\( (x_1,y_1) = (a\sec\theta,\ b\tan\theta) \)
The equation of normal is:
\( a x \cos\theta – b y \sin\theta = a^2 – b^2 \)
This is the most used formula in JEE advanced-style problems.
3. Normal in Slope Form
If normal has slope \( m \), then the contact point satisfies:
\( m = -\dfrac{a^2 y_1}{b^2 x_1} \)
Using substitution from parametric form gives nonlinear equations. But the final slope form of normal can be written as:
\( y = mx \pm\sqrt{a^2 + b^2 m^2} \)
This is used for locus problems.
4. Number of Normals from a Point
- From most external points, one real normal can be drawn.
- From some points, three normals can exist (similar to ellipse).
- From points on asymptotes, behavior must be checked via limits.
5. Key Identities Involving Normal
- Normal parameter \( \theta \) for hyperbola typically solves a cubic equation → leads to 1 or 3 solutions.
- Normal is very powerful for advanced coordinate geometry and locus questions.
Example
Find the equation of normal to the hyperbola \( \dfrac{x^2}{9}-\dfrac{y^2}{4}=1 \) at point \( (3,2) \).
▶️ Answer / Explanation
Slope of normal:
\( m_n = -\dfrac{a^2 y_1}{b^2 x_1} = -\dfrac{9\cdot 2}{4\cdot 3} = -\dfrac{18}{12} = -\dfrac{3}{2} \)
Normal equation:
\( y – 2 = -\dfrac{3}{2}(x – 3) \)
Answer: \( y – 2 = -\dfrac{3}{2}(x – 3) \)
Example
Find the equation of normal at parametric point \( \theta = \dfrac{\pi}{4} \) on \( \dfrac{x^2}{25}-\dfrac{y^2}{16}=1. \)
▶️ Answer / Explanation
Parametric normal:
\( a x \cos\theta – b y \sin\theta = a^2 – b^2 \)
Here \( a=5,\ b=4 \).
\( \cos\frac{\pi}{4}=\frac{1}{\sqrt{2}},\quad \sin\frac{\pi}{4}=\frac{1}{\sqrt{2}} \)
Thus:
\( 5x\cdot\dfrac{1}{\sqrt{2}} – 4y\cdot\dfrac{1}{\sqrt{2}} = 25 – 16 = 9 \)
Multiply both sides by \( \sqrt{2} \):
\( 5x – 4y = 9\sqrt{2} \)
Answer: \( 5x – 4y = 9\sqrt{2} \)
Example
Find the locus of foot of normal drawn from point \( P(0,c) \) to the hyperbola \( \dfrac{x^2}{a^2}-\dfrac{y^2}{b^2}=1. \)
▶️ Answer / Explanation
Let foot of normal be parametric point:
\( (a\sec\theta,\ b\tan\theta) \)
Normal equation:
\( a x \cos\theta – b y \sin\theta = a^2 – b^2 \)
Point \( P(0,c) \) lies on normal → substitute:
\( a(0)\cos\theta – b(c)\sin\theta = a^2 – b^2 \)
\( -bc\sin\theta = a^2 – b^2 \)
\( \sin\theta = -\dfrac{a^2 – b^2}{bc} \)
Using point coordinates:
\( x = a\sec\theta,\quad y = b\tan\theta \)
Thus:
\( \sec\theta = \dfrac{x}{a} \)
And:
\( \tan\theta = \dfrac{y}{b} \)
Using identity: \( \sin\theta = \dfrac{\tan\theta}{\sec\theta} = \dfrac{y/a}{x/b} = \dfrac{by}{ax} \)
Now equate with earlier value:
\( \dfrac{by}{ax} = -\dfrac{a^2 – b^2}{bc} \)
Cross multiply:
\( b^2 y = -a x (a^2 – b^2)/c \)
Final locus:
\( b^2 y + \dfrac{a(a^2 – b^2)}{c} x = 0 \)
Answer: Locus is a straight line \( b^2 y + \dfrac{a(a^2 – b^2)}{c} x = 0 \)
Hyperbola: Asymptotes
Asymptotes are straight lines that the branches of a hyperbola approach infinitely but never touch. They give the hyperbola its characteristic shape and are extremely important in curve sketching and tangent problems.
Standard hyperbola: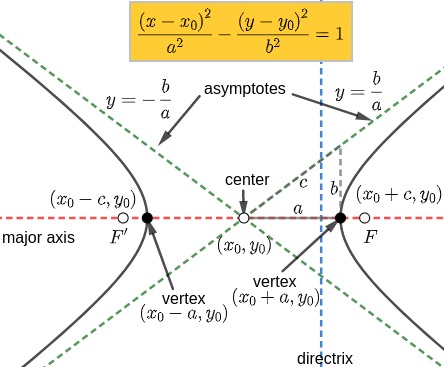
\( \dfrac{x^2}{a^2}-\dfrac{y^2}{b^2}=1 \)
1. Finding Asymptotes of Standard Hyperbola
Start from:
\( \dfrac{x^2}{a^2}-\dfrac{y^2}{b^2}=1 \)
As \( x \to \infty \): the “1” on right-hand side becomes negligible. So approximately:
\( \dfrac{x^2}{a^2}-\dfrac{y^2}{b^2} \approx 0 \)
Multiply by \(a^2 b^2\):
\( b^2 x^2 – a^2 y^2 = 0 \)
Factor:
\( (bx – ay)(bx + ay) = 0 \)
Thus asymptotes are:
\( y = \pm\dfrac{b}{a}x \)
2. Asymptotes of Vertical Hyperbola
For hyperbola:
\( \dfrac{y^2}{a^2}-\dfrac{x^2}{b^2}=1 \)
Asymptotes become:
\( y = \pm\dfrac{a}{b}x \)
3. Asymptotes of Shifted Hyperbola
If center is shifted to \( (h,k) \), equation becomes:
\( \dfrac{(x-h)^2}{a^2}-\dfrac{(y-k)^2}{b^2}=1 \)
Asymptotes are simply lines passing through \( (h,k) \):
\( y-k = \pm \dfrac{b}{a}(x-h) \)
4. Asymptotes of General Second-Degree Hyperbola
For conic:
\( Ax^2 + Bxy + Cy^2 + Dx + Ey + F = 0 \)
Asymptotes are found from the second-degree part:
\( Ax^2 + Bxy + Cy^2 = 0 \)
This gives two straight lines passing through center.
5. Relation Between Asymptotes and Eccentricity
If asymptote slope is \( \pm\dfrac{b}{a} \), eccentricity of hyperbola is:
\( e = \sqrt{1 + \dfrac{b^2}{a^2}} \)
since \( c^2 = a^2 + b^2 \) implies \( e = \dfrac{c}{a} = \sqrt{1 + \dfrac{b^2}{a^2}} \)
6. Angle Between Asymptotes
Let slopes be \( m_1 = \dfrac{b}{a} \) and \( m_2 = -\dfrac{b}{a} \).
Angle between them:
\( \theta = 2\tan^{-1}\left(\dfrac{b}{a}\right) \)
Important for JEE theory questions.
Example
Find asymptotes of hyperbola \( \dfrac{x^2}{9}-\dfrac{y^2}{4}=1. \)
▶️ Answer / Explanation
Here \( a=3,\ b=2 \).
Asymptotes:
\( y = \pm\dfrac{b}{a}x = \pm\dfrac{2}{3}x \)
Answer: \( y = \frac{2}{3}x,\quad y = -\frac{2}{3}x \)
Example
Find asymptotes of the vertical hyperbola \( \dfrac{y^2}{16}-\dfrac{x^2}{25}=1. \)
▶️ Answer / Explanation
\( a = 4,\ b = 5 \)
Asymptotes:
\( y = \pm\dfrac{a}{b}x = \pm\dfrac{4}{5}x \)
Answer: \( y = \frac{4}{5}x,\quad y = -\frac{4}{5}x \)
Example
Find the asymptotes of the hyperbola \( 4x^2 – 9y^2 – 40x + 54y – 84 = 0. \)
▶️ Answer / Explanation
Only the second-degree terms determine asymptotes:
\( 4x^2 – 9y^2 = 0 \)
Factor:
\( (2x – 3y)(2x + 3y) = 0 \)
Thus two asymptotes:
\( 2x – 3y = 0 \)
\( 2x + 3y = 0 \)
Or slope form:
\( y = \frac{2}{3}x,\quad y = -\frac{2}{3}x \)
Answer: Asymptotes are \( 2x – 3y = 0 \) and \( 2x + 3y = 0 \)
