IIT JEE Main Maths -Unit 11- Direction ratios and cosines- Study Notes-New Syllabus
IIT JEE Main Maths -Unit 11- Direction ratios and cosines – Study Notes – New syllabus
IIT JEE Main Maths -Unit 11- Direction ratios and cosines – Study Notes -IIT JEE Main Maths – per latest Syllabus.
Key Concepts:
- Direction Ratios and Direction Cosines
- Foot of Perpendicular From a Point to a Plane
- Projection of a Line on a Plane
- Reflection of a Point in a Plane
Direction Ratios and Direction Cosines
In three dimensional geometry, a line in space has a specific orientation. This orientation is represented using either direction ratios or direction cosines. Both play a fundamental role in constructing equations of lines and planes.
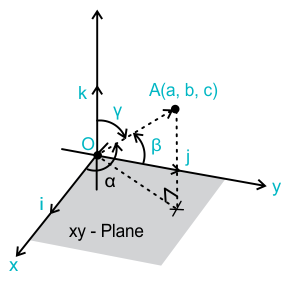
Direction Ratios (DRs)
If a line is parallel to a vector having components \( (a, b, c) \), then numbers proportional to \( a,\; b,\; c \) are called its direction ratios.
- Direction ratios need not be unique.
- If \( (a, b, c) \) are direction ratios, then \( (ka, kb, kc) \) are also direction ratios for any non zero constant \( k \).
- Direction ratios only give direction, not magnitude.
Direction Cosines (DCs)
Let a line make angles \( \alpha,\; \beta,\; \gamma \) with the positive \( X,\; Y,\; Z \) axes respectively. Then
- \( \cos\alpha \) is called direction cosine along X axis.
- \( \cos\beta \) is called direction cosine along Y axis.
- \( \cos\gamma \) is called direction cosine along Z axis.
If direction cosines are denoted by \( l,\; m,\; n \), then
\( l = \cos\alpha,\quad m = \cos\beta,\quad n = \cos\gamma \)
Relation Among Direction Cosines
The direction cosines satisfy the identity
\( l^2 + m^2 + n^2 = 1 \)
This comes from the property of a unit vector representing the direction of the line.
Relation Between Direction Ratios and Direction Cosines
If \( (a, b, c) \) are DRs and \( (l, m, n) \) are DCs of the same line, then
\( l = \dfrac{a}{\sqrt{a^2 + b^2 + c^2}},\quad m = \dfrac{b}{\sqrt{a^2 + b^2 + c^2}},\quad n = \dfrac{c}{\sqrt{a^2 + b^2 + c^2}} \)
Thus DRs give the vector and DCs give the unit vector in the same direction.
Converting DCs to DRs
If direction cosines are \( l, m, n \) then direction ratios are any proportional set
\( (a, b, c) = (kl,\; km,\; kn) \) for any non zero constant \( k \).
Important Notes for JEE
- DCs are unique but DRs are not.
- A line has infinite DR sets but only one set of DCs.
- If any of the direction cosines is negative, it means the line forms an obtuse angle with that axis.
- DCs always satisfy \( l^2 + m^2 + n^2 = 1 \).
- DRs of a line joining two points \( A(x_1, y_1, z_1) \) and \( B(x_2, y_2, z_2) \) are \( (x_2 – x_1,\; y_2 – y_1,\; z_2 – z_1) \).
Examples
Example
Find the direction ratios of the line joining points \( A(2, 3, 5) \) and \( B(7, 11, 8) \).
▶️ Answer / Explanation
DRs are differences of coordinates.
\( a = 7 – 2 = 5 \)
\( b = 11 – 3 = 8 \)
\( c = 8 – 5 = 3 \)
Thus DRs are \( (5,\; 8,\; 3) \).
Example
If the direction ratios of a line are \( (6, -3, 2) \), find its direction cosines.
▶️ Answer / Explanation
First find the magnitude.
\( \sqrt{6^2 + (-3)^2 + 2^2} = \sqrt{36 + 9 + 4} = \sqrt{49} = 7 \)
So direction cosines are
\( l = \dfrac{6}{7},\quad m = \dfrac{-3}{7},\quad n = \dfrac{2}{7} \)
Example
Direction cosines of a line are \( l = \dfrac{3}{7},\; m = \dfrac{2}{7} \). Find \( n \) and also find one possible set of direction ratios.
▶️ Answer / Explanation
Use the identity
\( l^2 + m^2 + n^2 = 1 \)
\( \left( \dfrac{3}{7} \right)^2 + \left( \dfrac{2}{7} \right)^2 + n^2 = 1 \)
\( \dfrac{9}{49} + \dfrac{4}{49} + n^2 = 1 \)
\( \dfrac{13}{49} + n^2 = 1 \Rightarrow n^2 = \dfrac{36}{49} \)
\( n = \pm\dfrac{6}{7} \)
Now to find direction ratios choose any constant \( k \). Let \( k = 7 \).
If \( n = \dfrac{6}{7} \), DRs are \( (3,\; 2,\; 6) \)
If \( n = -\dfrac{6}{7} \), DRs are \( (3,\; 2,\; -6) \)
Foot of Perpendicular From a Point to a Plane
The foot of perpendicular is the point on a plane such that the line joining the given point and this point is perpendicular to the plane. This foot point is extremely useful in 3D geometry, vector projection problems, shortest distance questions, and coordinate geometry proofs.
Concept
You are given:
- A point \( P(x_1, y_1, z_1) \)
- A plane \( ax + by + cz + d = 0 \)
The foot of perpendicular \( F(x_0, y_0, z_0) \) lies on the plane and satisfies:
- The vector \( \overrightarrow{PF} \) is parallel to the normal vector \( (a, b, c) \).
Formula for Foot of Perpendicular
The coordinates of the foot of perpendicular from \( P(x_1, y_1, z_1) \) to plane \( ax + by + cz + d = 0 \) are
\( x_0 = x_1 – \dfrac{a(ax_1 + by_1 + cz_1 + d)}{a^2 + b^2 + c^2} \)
\( y_0 = y_1 – \dfrac{b(ax_1 + by_1 + cz_1 + d)}{a^2 + b^2 + c^2} \)
\( z_0 = z_1 – \dfrac{c(ax_1 + by_1 + cz_1 + d)}{a^2 + b^2 + c^2} \)
Vector Form (Quick Idea)
\( \vec{OF} = \vec{OP} – \dfrac{\vec{n} \cdot \vec{OP} + d}{|\vec{n}|^2} \vec{n} \)
Very useful in vector-based JEE questions.
Important Notes
- Foot point lies on the plane, so it satisfies plane equation.
- Direction from \( P \) to the foot point is parallel to normal vector.
- Used in reflection questions, distance questions, and plane geometry problems.
Example
Find the foot of perpendicular from point \( P(2, 3, 4) \) to the plane \( x + y + z – 6 = 0 \).
▶️ Answer / Explanation
Compute:
\( ax_1 + by_1 + cz_1 + d = 2 + 3 + 4 – 6 = 3 \)
\( a^2 + b^2 + c^2 = 1 + 1 + 1 = 3 \)
Coordinates:
\( x_0 = 2 – \dfrac{1\cdot3}{3} = 1 \)
\( y_0 = 3 – \dfrac{1\cdot3}{3} = 2 \)
\( z_0 = 4 – \dfrac{1\cdot3}{3} = 3 \)
Foot point = \( (1, 2, 3) \)
Example
Find the foot of perpendicular from point \( P(1, -2, 3) \) to plane \( 2x – y + 2z + 1 = 0 \).
▶️ Answer / Explanation
Compute:
\( ax_1 + by_1 + cz_1 + d = 2(1) -1(-2) + 2(3) + 1 = 2 + 2 + 6 + 1 = 11 \)
\( a^2 + b^2 + c^2 = 4 + 1 + 4 = 9 \)
Coordinates:
\( x_0 = 1 – \dfrac{2\cdot11}{9} = 1 – \dfrac{22}{9} = -\dfrac{13}{9} \)
\( y_0 = -2 – \dfrac{-1\cdot11}{9} = -2 + \dfrac{11}{9} = -\dfrac{7}{9} \)
\( z_0 = 3 – \dfrac{2\cdot11}{9} = 3 – \dfrac{22}{9} = \dfrac{5}{9} \)
Foot point = \( \left( -\dfrac{13}{9}, -\dfrac{7}{9}, \dfrac{5}{9} \right) \)
Example
Find the foot of perpendicular from point \( P(4, -1, 2) \) to the plane passing through points \( A(1, 0, 2) \), \( B(3, -1, 4) \), \( C(5, 2, 1) \).
▶️ Answer / Explanation
Step 1: Find plane normal using cross product.
\( \overrightarrow{AB} = (2, -1, 2) \)
\( \overrightarrow{AC} = (4, 2, -1) \)
\( \vec{n} = \overrightarrow{AB} \times \overrightarrow{AC} = \begin{vmatrix} \hat{i} & \hat{j} & \hat{k} \\ 2 & -1 & 2 \\ 4 & 2 & -1 \end{vmatrix} \)
\( = \hat{i}((-1)(-1) – 2\cdot2) – \hat{j}(2(-1) – 2\cdot4) + \hat{k}(2\cdot2 – (-1)4) \)
\( = (1 – 4,\; -(-2 – 8),\; 4 + 4) = (-3,\; 10,\; 8) \)
Step 2: Find plane equation using point A.
\( -3(x – 1) + 10(y – 0) + 8(z – 2) = 0 \)
\( -3x + 3 + 10y + 8z – 16 = 0 \)
\( -3x + 10y + 8z – 13 = 0 \)
Step 3: Use foot of perpendicular formula.
Compute:
\( ax_1 + by_1 + cz_1 + d = -3(4) + 10(-1) + 8(2) – 13 \)
\( = -12 – 10 + 16 – 13 = -19 \)
\( a^2 + b^2 + c^2 = 9 + 100 + 64 = 173 \)
Coordinates:
\( x_0 = 4 – \dfrac{-3(-19)}{173} = 4 – \dfrac{57}{173} = \dfrac{692 – 57}{173} = \dfrac{635}{173} \)
\( y_0 = -1 – \dfrac{10(-19)}{173} = -1 + \dfrac{190}{173} = \dfrac{17}{173} \)
\( z_0 = 2 – \dfrac{8(-19)}{173} = 2 + \dfrac{152}{173} = \dfrac{346 + 152}{173} = \dfrac{498}{173} \)
Foot point = \( \left( \dfrac{635}{173},\; \dfrac{17}{173},\; \dfrac{498}{173} \right) \)
Projection of a Line on a Plane
The projection of a line on a plane is the line you get when every point on the line is dropped perpendicularly onto the plane. The direction of this projected line depends on how the original line is oriented relative to the plane.
If a line has direction vector \( \vec{d} = (a, b, c) \), and the plane has normal vector \( \vec{n} = (A, B, C) \), then the component of \( \vec{d} \) along the plane is the projection of \( \vec{d} \) on the plane.
Direction Vector of the Projected Line
The direction vector of the projection of a line on a plane is
\( \vec{d_{\text{proj}}} = \vec{d} – \dfrac{\vec{d} \cdot \vec{n}}{|\vec{n}|^2}\, \vec{n} \)
- This formula removes the component of the vector perpendicular to the plane.
- The remaining component lies inside the plane, giving the direction of projection.
Angle Use: Projection Length
Angle between line and plane = \( \theta \). If the line has length \( L \), then its projection on the plane has length:
\( L_{\text{proj}} = L \cos\theta \)
Since
\( \sin\theta = \dfrac{| \vec{d} \cdot \vec{n} |}{|\vec{d}|\, |\vec{n}|} \)
we get
\( \cos\theta = \sqrt{1 – \sin^2\theta} \)
Equation of the Projected Line
Once you get the projected direction vector \( \vec{d_{\text{proj}}} \), choose any point from the original line (usually its given point). Use parametric or symmetric form:
Projected Line: \( x = x_1 + p\lambda,\; y = y_1 + q\lambda,\; z = z_1 + r\lambda \)
where \( (p, q, r) = \vec{d_{\text{proj}}} \).
Example
Find the direction vector of projection of line \( \vec{d} = (1, 2, 3) \) on the plane with normal vector \( \vec{n} = (1, 1, 1) \).
▶️ Answer / Explanation
Compute dot product:
\( \vec{d} \cdot \vec{n} = 1 + 2 + 3 = 6 \)
\( |\vec{n}|^2 = 1^2 + 1^2 + 1^2 = 3 \)
Projected vector:
\( \vec{d_{\text{proj}}} = (1, 2, 3) – \dfrac{6}{3}(1, 1, 1) \)
\( = (1, 2, 3) – 2(1, 1, 1) = (-1, 0, 1) \)
Projection direction vector = \( (-1, 0, 1) \).
Example
Find the projection of the line \( \vec{r} = (2, -1, 3) + \lambda(2, 1, -2) \) on the plane \( x – 2y + 2z = 5 \).
▶️ Answer / Explanation
Direction vector of line:
\( \vec{d} = (2, 1, -2) \)
Normal vector of plane:
\( \vec{n} = (1, -2, 2) \)
Compute dot product:
\( \vec{d} \cdot \vec{n} = 2(1) + 1(-2) + (-2)2 = 2 – 2 – 4 = -4 \)
\( |\vec{n}|^2 = 1^2 + (-2)^2 + 2^2 = 9 \)
Projection direction vector:
\( \vec{d_{\text{proj}}} = (2, 1, -2) – \dfrac{-4}{9}(1, -2, 2) \)
\( = (2, 1, -2) + \left( \dfrac{4}{9}, -\dfrac{8}{9}, \dfrac{8}{9} \right) \)
\( = \left( \dfrac{22}{9}, \dfrac{1}{9}, -\dfrac{10}{9} \right) \)
Thus projected line is
\( x = 2 + \dfrac{22}{9}\lambda,\quad y = -1 + \dfrac{1}{9}\lambda,\quad z = 3 – \dfrac{10}{9}\lambda \)
Example
Find the equation of the projection of the line \( \dfrac{x – 1}{3} = \dfrac{y + 2}{2} = \dfrac{z – 4}{1} \) on the plane \( 2x + y – 2z + 3 = 0 \).
▶️ Answer / Explanation
Step 1: Identify components.
Direction vector of line:
\( \vec{d} = (3, 2, 1) \)
Normal vector of plane:
\( \vec{n} = (2, 1, -2) \)
Point on line:
\( P(1, -2, 4) \)
Step 2: Find projection direction vector.
\( \vec{d} \cdot \vec{n} = 3(2) + 2(1) + 1(-2) = 6 + 2 – 2 = 6 \)
\( |\vec{n}|^2 = 2^2 + 1^2 + (-2)^2 = 9 \)
\( \vec{d_{\text{proj}}} = (3, 2, 1) – \dfrac{6}{9}(2, 1, -2) \)
\( = (3, 2, 1) – \left( \dfrac{4}{3}, \dfrac{2}{3}, -\dfrac{4}{3} \right) \)
\( = \left( \dfrac{5}{3}, \dfrac{4}{3}, \dfrac{7}{3} \right) \)
Step 3: Write projected line equation.
Use point \( P(1, -2, 4) \) and projected direction vector.
\( x = 1 + \dfrac{5}{3}\lambda \)
\( y = -2 + \dfrac{4}{3}\lambda \)
\( z = 4 + \dfrac{7}{3}\lambda \)
This is the equation of the projected line.
Reflection of a Point in a Plane
The reflection of a point across a plane is the point obtained by moving the original point perpendicularly across the plane by the same distance. The plane acts like a mirror.
Concept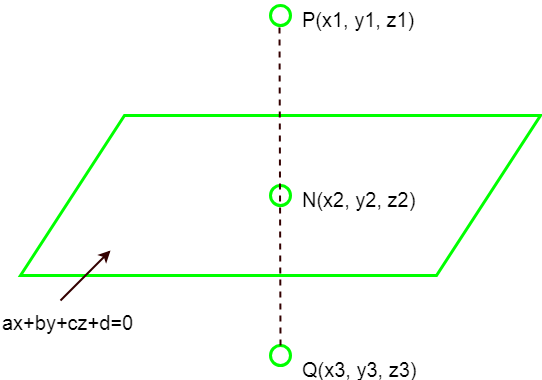
Let a point be \( P(x_1, y_1, z_1) \). Let the plane be
\( ax + by + cz + d = 0 \)
The foot of perpendicular from \( P \) to the plane is \( F(x_0, y_0, z_0) \).
The reflected point \( P’ \) is such that:
- \( F \) is the midpoint of segment \( PP’ \)
- \( \overrightarrow{PF} \) is parallel to normal vector \( (a, b, c) \)
Reflection Formula
First compute
\( k = \dfrac{ax_1 + by_1 + cz_1 + d}{a^2 + b^2 + c^2} \)
Then reflected point \( P'(x’, y’, z’) \) is
\( x’ = x_1 – 2ak \)
\( y’ = y_1 – 2bk \)
\( z’ = z_1 – 2ck \)
Key Notes
- If point lies on plane, reflection is same point.
- Reflection preserves perpendicular distance to plane.
- Useful in locus, geometry proofs, and vector transformations.
- Reflection can also be done by doubling the displacement from foot.
Example
Find the reflection of point \( P(2, 3, 4) \) in the plane \( x + y + z – 6 = 0 \).
▶️ Answer / Explanation
Compute:
\( k = \dfrac{2 + 3 + 4 – 6}{1 + 1 + 1} = \dfrac{3}{3} = 1 \)
Reflection:
\( x’ = 2 – 2(1)(1) = 0 \)
\( y’ = 3 – 2(1)(1) = 1 \)
\( z’ = 4 – 2(1)(1) = 2 \)
Reflected point = \( (0, 1, 2) \)
Example
Find the reflection of point \( P(1, -2, 3) \) in plane \( 2x – y + 2z + 1 = 0 \).
▶️ Answer / Explanation
\( k = \dfrac{2(1) -(-2) + 2(3) + 1}{4 + 1 + 4} = \dfrac{2 + 2 + 6 + 1}{9} = \dfrac{11}{9} \)
Compute reflected coordinates:
\( x’ = 1 – 2(2)\left( \dfrac{11}{9} \right) = 1 – \dfrac{44}{9} = -\dfrac{35}{9} \)
\( y’ = -2 – 2(-1)\left( \dfrac{11}{9} \right) = -2 + \dfrac{22}{9} = \dfrac{4}{9} \)
\( z’ = 3 – 2(2)\left( \dfrac{11}{9} \right) = 3 – \dfrac{44}{9} = -\dfrac{17}{9} \)
Reflected point = \( \left( -\dfrac{35}{9},\; \dfrac{4}{9},\; -\dfrac{17}{9} \right) \)
Example
Find the reflection of point \( P(4, -1, 2) \) across the plane passing through points \( A(1, 0, 2) \), \( B(3, -1, 4) \), \( C(5, 2, 1) \).
▶️ Answer / Explanation
Step 1: Find plane equation
\( \overrightarrow{AB} = (2, -1, 2) \)
\( \overrightarrow{AC} = (4, 2, -1) \)
Normal vector:
\( \vec{n} = \begin{vmatrix} \hat{i} & \hat{j} & \hat{k} \\ 2 & -1 & 2 \\ 4 & 2 & -1 \end{vmatrix} = (-3, 10, 8) \)
Plane through A:
\( -3(x – 1) + 10(y – 0) + 8(z – 2) = 0 \)
\( -3x + 10y + 8z – 13 = 0 \)
Step 2: Find k
\( k = \dfrac{-3(4) + 10(-1) + 8(2) – 13}{9 + 100 + 64} \)
\( = \dfrac{-12 – 10 + 16 – 13}{173} = \dfrac{-19}{173} \)
Step 3: Reflection coordinates
\( x’ = 4 – 2(-3)\left( \dfrac{-19}{173} \right) = 4 – \dfrac{114}{173} = \dfrac{692 – 114}{173} = \dfrac{578}{173} \)
\( y’ = -1 – 2(10)\left( \dfrac{-19}{173} \right) = -1 + \dfrac{380}{173} = \dfrac{207}{173} \)
\( z’ = 2 – 2(8)\left( \dfrac{-19}{173} \right) = 2 + \dfrac{304}{173} = \dfrac{650}{173} \)
Reflected point = \( \left( \dfrac{578}{173},\; \dfrac{207}{173},\; \dfrac{650}{173} \right) \)
