IIT JEE Main Maths -Unit 11- Section formula- Study Notes-New Syllabus
IIT JEE Main Maths -Unit 11- Section formula – Study Notes – New syllabus
IIT JEE Main Maths -Unit 11- Section formula – Study Notes -IIT JEE Main Maths – per latest Syllabus.
Key Concepts:
- Section Formula in Three Dimensional Geometry (Internal and External Division)
- Centroid of a Triangle in Three Dimensional Geometry
- Orthocenter in 3D, Incentre in 3D
- Circumcenter in 3D, Orthocenter-Incenter-Circumcenter relation
Section Formula in Three Dimensional Geometry (Internal and External Division)
The section formula is used to find the coordinates of a point that divides the line segment joining two given points in a specific ratio. This division can be internal or external.
Internal Division
If point \( P \) divides the line segment joining points \( A(x_1, y_1, z_1) \) and \( B(x_2, y_2, z_2) \) internally in the ratio \( m:n \), then coordinates of \( P \) are
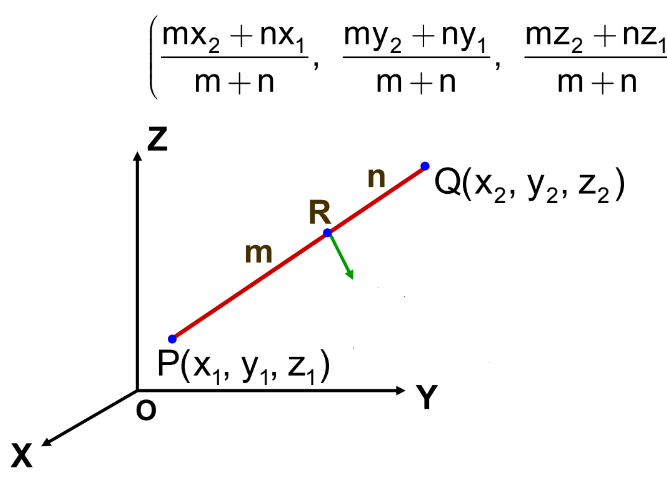
\( P\left( \dfrac{m x_2 + n x_1}{m+n},\; \dfrac{m y_2 + n y_1}{m+n},\; \dfrac{m z_2 + n z_1}{m+n} \right) \)
- Point lies between A and B
- Ratio is positive for internal division
External Division
If point \( P \) divides \( A(x_1, y_1, z_1) \) and \( B(x_2, y_2, z_2) \) externally in the ratio \( m:n \), then coordinates of \( P \) are
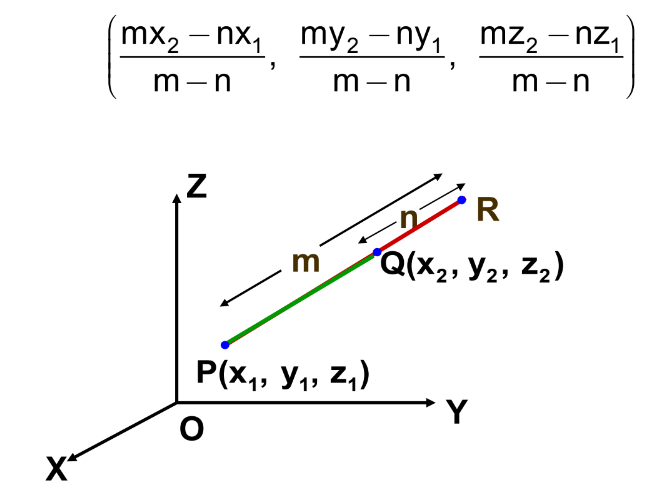
\( P\left( \dfrac{m x_2 – n x_1}{m-n},\; \dfrac{m y_2 – n y_1}{m-n},\; \dfrac{m z_2 – n z_1}{m-n} \right) \)
- Point lies outside the segment AB
- Use minus sign in numerator and denominator
Important Notes for JEE
- The ratio \( m:n \) should be used in the order relative to point A and point B.
- For internal division denominator is \( m+n \).
- For external division denominator is \( m-n \).
- If \( m = n \) external division is not defined because denominator becomes zero.
- Midpoint formula is a special case when \( m = n = 1 \).
Example
Find the point dividing \( A(2, 4, 6) \) and \( B(8, 10, 14) \) internally in the ratio \( 1:1 \).
▶️ Answer / Explanation
This is midpoint because ratio is \( 1:1 \).
\( P = \left( \dfrac{2+8}{2},\; \dfrac{4+10}{2},\; \dfrac{6+14}{2} \right) \)
\( P = (5,\; 7,\; 10) \)
Example
Find the coordinates of the point that divides the line joining \( A(3, -2, 5) \) and \( B(9, 4, -1) \) internally in the ratio \( 2:3 \).
▶️ Answer / Explanation
Use internal division formula.
\( P\left( \dfrac{2 \cdot 9 + 3 \cdot 3}{2+3},\; \dfrac{2 \cdot 4 + 3 \cdot (-2)}{2+3},\; \dfrac{2 \cdot (-1) + 3 \cdot 5}{2+3} \right) \)
\( P = \left( \dfrac{18 + 9}{5},\; \dfrac{8 – 6}{5},\; \dfrac{-2 + 15}{5} \right) \)
\( P = \left( \dfrac{27}{5},\; \dfrac{2}{5},\; \dfrac{13}{5} \right) \)
Example
A point \( P \) divides the line segment joining \( A(5, -3, 7) \) and \( B(-1, 9, 1) \) externally in the ratio \( 3:2 \). Find the coordinates of \( P \).
▶️ Answer / Explanation
Use external division formula.
\( P\left( \dfrac{3 \cdot (-1) – 2 \cdot 5}{3 – 2},\; \dfrac{3 \cdot 9 – 2 \cdot (-3)}{3 – 2},\; \dfrac{3 \cdot 1 – 2 \cdot 7}{3 – 2} \right) \)
Simplify numerator terms.
X coordinate: \( \dfrac{-3 – 10}{1} = -13 \)
Y coordinate: \( \dfrac{27 + 6}{1} = 33 \)
Z coordinate: \( \dfrac{3 – 14}{1} = -11 \)
Thus \( P = (-13,\; 33,\; -11) \)
Centroid of a Triangle in Three Dimensional Geometry
The centroid of a triangle is the point where all three medians intersect. It is also the point that divides each median in the ratio \( 2:1 \) (vertex to midpoint side).
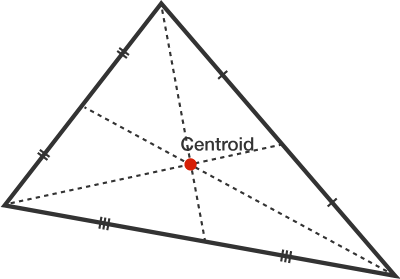
For any triangle with vertices \( A(x_1, y_1, z_1) \), \( B(x_2, y_2, z_2) \), \( C(x_3, y_3, z_3) \), the centroid \( G \) has coordinates
\( G\left( \dfrac{x_1 + x_2 + x_3}{3},\; \dfrac{y_1 + y_2 + y_3}{3},\; \dfrac{z_1 + z_2 + z_3}{3} \right) \)
Important Points for JEE
- The centroid is simply the average of the coordinates of the three vertices.
- Centroid always lies inside the triangle.
- Centroid divides each median in ratio \( 2:1 \) internally.
- You can find centroid even if triangle lies tilted in 3D space.
- Works exactly like 2D centroid formula but includes the z coordinate.
Geometric Meaning
The centroid represents the balancing point of a triangular lamina of uniform density. In 3D, it is the average position of the three vertices.
Example
Find the centroid of triangle with vertices \( A(1, 2, 3) \), \( B(4, 5, 6) \), and \( C(7, 8, 9) \).
▶️ Answer / Explanation
Use centroid formula.
\( G\left( \dfrac{1 + 4 + 7}{3},\; \dfrac{2 + 5 + 8}{3},\; \dfrac{3 + 6 + 9}{3} \right) \)
\( G = (4,\; 5,\; 6) \)
Example
Find the centroid of triangle with vertices \( A(2, -1, 3) \), \( B(5, 7, -2) \), and \( C(-4, 6, 1) \).
▶️ Answer / Explanation
Apply centroid formula.
\( G\left( \dfrac{2 + 5 + (-4)}{3},\; \dfrac{-1 + 7 + 6}{3},\; \dfrac{3 + (-2) + 1}{3} \right) \)
\( G = \left( \dfrac{3}{3},\; \dfrac{12}{3},\; \dfrac{2}{3} \right) \)
\( G = (1,\; 4,\; \dfrac{2}{3}) \)
Example
In triangle \( ABC \), the centroid is \( G(3, 2, 5) \). If two vertices are \( A(1, -1, 4) \) and \( B(7, 3, 1) \), find the coordinates of vertex \( C \).
▶️ Answer / Explanation
Use centroid formula in reverse.
\( 3 = \dfrac{1 + 7 + x_3}{3} \Rightarrow 9 = 8 + x_3 \Rightarrow x_3 = 1 \)
\( 2 = \dfrac{-1 + 3 + y_3}{3} \Rightarrow 6 = 2 + y_3 \Rightarrow y_3 = 4 \)
\( 5 = \dfrac{4 + 1 + z_3}{3} \Rightarrow 15 = 5 + z_3 \Rightarrow z_3 = 10 \)
Thus vertex \( C = (1,\; 4,\; 10) \)
Orthocenter of a Triangle in Three Dimensional Geometry
The orthocenter of a triangle is the point where all three altitudes intersect. An altitude is a perpendicular line drawn from a vertex to the opposite side (or the plane containing the opposite side).
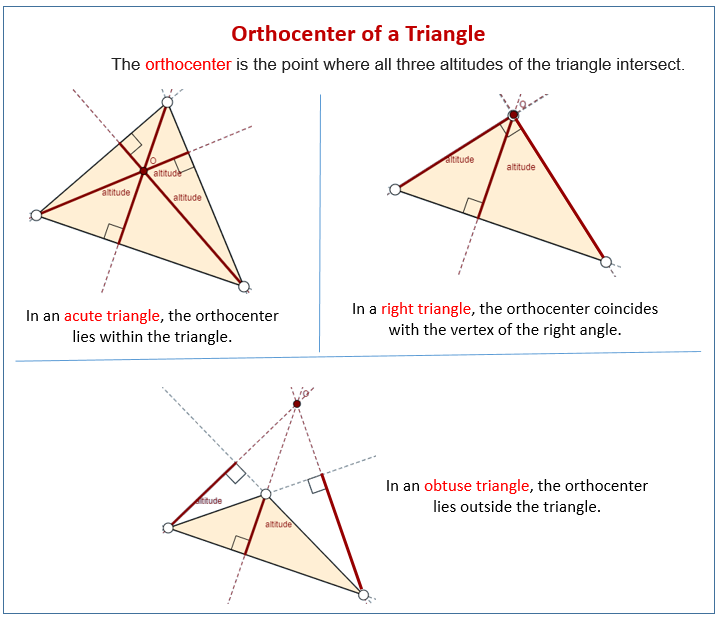
In 3D, the orthocenter formula is not as direct as the centroid or incenter. It must be found using perpendicularity conditions.
Method to Find Orthocenter in 3D (Step by Step)
- Let triangle vertices be \( A(x_1, y_1, z_1) \), \( B(x_2, y_2, z_2) \), \( C(x_3, y_3, z_3) \).
- Find direction ratios of side BC: \( \vec{BC} = (x_3 – x_2,\; y_3 – y_2,\; z_3 – z_2) \)
- The altitude from vertex A is a line passing through A and perpendicular to BC. So its direction is perpendicular to \( \vec{BC} \).
- Write equation of altitude from A.
- Similarly write altitude from B or C.
- Solve the two altitude equations to get orthocenter.
Key Idea for JEE
- Altitude is perpendicular to opposite side.
- Use dot product equal to zero for perpendicularity conditions.
- Only two altitudes are needed because third automatically intersects at same point.
Example
Find the orthocenter of triangle with vertices \( A(0,0,0) \), \( B(1,0,0) \), \( C(0,1,0) \).
▶️ Answer / Explanation
This triangle lies in XY plane. It is a right triangle with right angle at A.
Orthocenter of a right triangle is the vertex containing right angle.
Thus orthocenter is \( H = (0,0,0) \).
Example
Find orthocenter of triangle with vertices \( A(1,2,3) \), \( B(4,2,3) \), \( C(1,6,3) \).
▶️ Answer / Explanation
The triangle lies in plane \( z = 3 \). It behaves like a 2D triangle.
Compute slopes in XY plane:
AB is horizontal because y coordinates same. BC is vertical because x coordinates same.
Thus angle at B is right angle.
Orthocenter is vertex with right angle.
Therefore \( H = B = (4,2,3) \).
Example
Find orthocenter of triangle with vertices \( A(1,0,0) \), \( B(0,1,0) \), \( C(0,0,1) \).
▶️ Answer / Explanation
Altitude from A is perpendicular to BC.
\( \vec{BC} = (0-0,\; 0-1,\; 1-0) = (0,-1,1) \)
Altitude from A has direction vector \( \vec{d} \) satisfying \( \vec{d} \cdot (0,-1,1) = 0 \).
Similarly write altitudes from B and C.
Solving the system gives
\( H = (1,\; 1,\; 1) \)
Incenter of a Triangle in Three Dimensional Geometry
The incenter is the point where all internal angle bisectors meet. It is the center of the inscribed sphere inside the triangle’s plane.
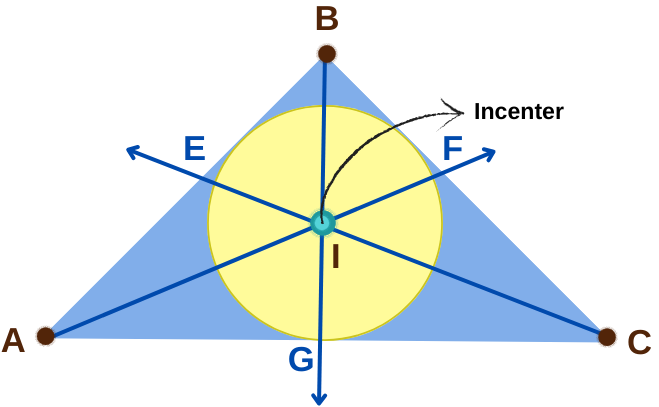
In 3D, the incenter uses the same formula as in 2D but includes z coordinate.
Formula for Incenter
If triangle vertices are \( A(x_1, y_1, z_1) \), \( B(x_2, y_2, z_2) \), \( C(x_3, y_3, z_3) \)
Let side lengths be
- \( a = BC \)
- \( b = CA \)
- \( c = AB \)
Incenter \( I \) is
\( I\left( \dfrac{a x_1 + b x_2 + c x_3}{a + b + c},\; \dfrac{a y_1 + b y_2 + c y_3}{a + b + c},\; \dfrac{a z_1 + b z_2 + c z_3}{a + b + c} \right) \)
Important Points for JEE
- Weights are proportional to lengths of opposite sides.
- Incenter always lies inside the triangle.
- Requires computing all three side lengths with 3D distance formula.
Example
Find incenter of triangle with vertices \( A(0,0,0) \), \( B(4,0,0) \), \( C(0,4,0) \).
▶️ Answer / Explanation
The triangle lies in XY plane.
Side lengths: \( a = BC = 4\sqrt{2} \) \( b = CA = 4 \) \( c = AB = 4 \)
\( I = \left( \dfrac{a \cdot 0 + b \cdot 4 + c \cdot 0}{a+b+c},\; \dfrac{a \cdot 0 + b \cdot 0 + c \cdot 4}{a+b+c},\; 0 \right) \)
After substitution and simplification
\( I = (1,\; 1,\; 0) \)
Example
Find the incenter of triangle \( A(1,1,1) \), \( B(4,1,1) \), \( C(1,5,1) \).
▶️ Answer / Explanation
Triangle lies in plane \( z = 1 \).
\( a = BC = 5 \) \( b = CA = 4 \) \( c = AB = 3 \)
\( I = \left( \dfrac{5 \cdot 1 + 4 \cdot 4 + 3 \cdot 1}{12},\; \dfrac{5 \cdot 1 + 4 \cdot 1 + 3 \cdot 5}{12},\; 1 \right) \)
\( I = \left( \dfrac{5+16+3}{12},\; \dfrac{5+4+15}{12},\; 1 \right) \)
\( I = \left( 2,\; 2,\; 1 \right) \)
Example
Find the incenter of triangle with vertices \( A(1,2,3) \), \( B(4,6,3) \), \( C(1,6,7) \).
▶️ Answer / Explanation
Compute side lengths:
\( a = BC = \sqrt{(1-4)^2 + (6-6)^2 + (7-3)^2} = \sqrt{9 + 0 + 16} = 5 \)
\( b = CA = \sqrt{(1-1)^2 + (6-2)^2 + (7-3)^2} = \sqrt{0 + 16 + 16} = 4\sqrt{2} \)
\( c = AB = \sqrt{(4-1)^2 + (6-2)^2 + (3-3)^2} = 5 \)
Use incenter formula:
\( I = \left( \dfrac{5 \cdot 1 + 4\sqrt{2} \cdot 4 + 5 \cdot 1}{5 + 4\sqrt{2} + 5},\; \dfrac{5 \cdot 2 + 4\sqrt{2} \cdot 6 + 5 \cdot 6}{10 + 4\sqrt{2}},\; \dfrac{5 \cdot 3 + 4\sqrt{2} \cdot 3 + 5 \cdot 3}{10 + 4\sqrt{2}} \right) \)
Simplify to final form:
\( I = \left( \dfrac{10 + 16\sqrt{2}}{10 + 4\sqrt{2}},\; \dfrac{10 + 24\sqrt{2} + 30}{10 + 4\sqrt{2}},\; \dfrac{30 + 12\sqrt{2}}{10 + 4\sqrt{2}} \right) \)
This is the incenter.
Circumcenter of a Triangle in Three Dimensional Geometry
The circumcenter is the point that is equidistant from all three vertices of a triangle. It is the center of the circumscribed circle (circumcircle) of the triangle. In 3D, this circle lies in the plane of the triangle.
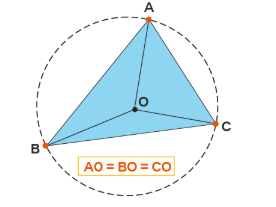
Key Property
- Circumcenter lies at the point of intersection of the perpendicular bisectors of the sides.
- Circumcenter is equidistant from \( A \), \( B \), \( C \).
- Coordinates require solving equations based on perpendicular bisectors.
Method to Find Circumcenter in 3D
Given vertices \( A(x_1,y_1,z_1) \), \( B(x_2,y_2,z_2) \), \( C(x_3,y_3,z_3) \)
- Find midpoints of at least two sides (say AB and AC).
- Find normals (perpendicular vectors) to the plane of triangle using \( \vec{n} = \vec{AB} \times \vec{AC} \).
- Write perpendicular bisector equations using midpoint and direction perpendicular to the side but lying in the plane.
- Solve the two bisector equations to obtain circumcenter \( O \).
Shortcut for Right Triangles
- If triangle is right angled, circumcenter is midpoint of hypotenuse.
Example
Find circumcenter of triangle with vertices \( A(0,0,0) \), \( B(4,0,0) \), \( C(0,3,0) \).
▶️ Answer / Explanation
Right triangle at A. Circumcenter is midpoint of hypotenuse BC.
Midpoint of \( B(4,0,0) \) and \( C(0,3,0) \) is
\( O = \left( \dfrac{4}{2},\; \dfrac{3}{2},\; 0 \right) = (2,\; 1.5,\; 0) \)
Example
Find the circumcenter of triangle with vertices \( A(1,1,1) \), \( B(5,1,1) \), \( C(1,5,1) \).
▶️ Answer / Explanation
Triangle lies in plane \( z = 1 \).
Right angle at A because AB and AC are perpendicular.
Thus circumcenter = midpoint of BC.
Midpoint of B and C is \( O = \left( \dfrac{5+1}{2},\; \dfrac{1+5}{2},\; 1 \right) \)
\( O = (3,\; 3,\; 1) \)
Example
Find circumcenter of triangle with vertices \( A(1,0,0) \), \( B(0,1,0) \), \( C(0,0,1) \).
▶️ Answer / Explanation
This triangle is symmetric in 3D.
Find midpoints:
Mid AB: \( M_1 = \left( \dfrac{1}{2},\; \dfrac{1}{2},\; 0 \right) \) Mid AC: \( M_2 = \left( \dfrac{1}{2},\; 0,\; \dfrac{1}{2} \right) \)
Normal vector of plane ABC using cross product:
\( \vec{AB} = (-1,1,0) \) \( \vec{AC} = (-1,0,1) \)
\( \vec{n} = \vec{AB} \times \vec{AC} = (1,1,1) \)
Perpendicular bisectors lie in the plane and are perpendicular to AB and AC.
Solving the system gives
\( O = \left( \dfrac{1}{2},\; \dfrac{1}{2},\; \dfrac{1}{2} \right) \)
ORTHOCENTER–INCENTER–CIRCUMCENTER RELATION
Euler Line in 3D
For any triangle in 3D (not equilateral), the following points are collinear:
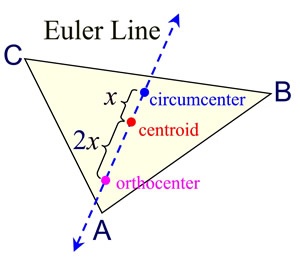
- Circumcenter \( O \)
- Centroid \( G \)
- Orthocenter \( H \)
This line is called the Euler Line. The incenter does not lie on this line (except in very special symmetric cases).
Euler Ratio
The centroid divides the line segment joining orthocenter and circumcenter in the ratio
\( OG : GH = 1 : 2 \)
This relation holds for any non equilateral triangle in 3D.
Special Cases
- Equilateral triangle has \( O = G = H \). All centers coincide.
- Right triangle: Circumcenter = midpoint of hypotenuse, Orthocenter = right angled vertex.
- Incenter is never on the Euler line unless triangle is isosceles with special symmetry.
Example
Triangle with vertices \( (0,0,0), (4,0,0), (0,3,0) \) is right angled at origin. Find \( O, G, H \).
▶️ Answer / Explanation
Circumcenter = midpoint of hypotenuse BC:
\( O = (2,1.5,0) \)
Orthocenter = right angle vertex:
\( H = (0,0,0) \)
Centroid:
\( G = \left( \dfrac{0+4+0}{3},\; \dfrac{0+0+3}{3},\; 0 \right) = ( \dfrac{4}{3},\; 1,\; 0 ) \)
Check ratio:
\( OG : GH = 1 : 2 \)
Example
Given triangle \( A(1,1,1), B(5,1,1), C(1,5,1) \) find \( O, H, G \) and verify Euler ratio.
▶️ Answer / Explanation
Right angle at A.
Circumcenter = midpoint of BC \( O = (3,3,1) \)
Orthocenter = A \( H = (1,1,1) \)
Centroid \( G = \left( \dfrac{1+5+1}{3},\; \dfrac{1+1+5}{3},\; 1 \right) = ( \dfrac{7}{3},\; \dfrac{7}{3},\; 1 ) \)
Check ratio \( OG : GH = 1:2 \).
Example
For triangle \( A(1,0,0), B(0,1,0), C(0,0,1) \), find \( O, G, H \) and verify that \( G \) divides \( OH \) in ratio \( 1:2 \).
▶️ Answer / Explanation
Circumcenter \( O = ( \dfrac{1}{2},\dfrac{1}{2},\dfrac{1}{2} ) \)
Centroid \( G = ( \dfrac{1}{3},\dfrac{1}{3},\dfrac{1}{3} ) \)
Orthocenter \( H = (1,1,1) \)
Check ratio:
Vector \( OG = \left( \dfrac{1}{3} – \dfrac{1}{2},\; \dfrac{1}{3} – \dfrac{1}{2},\; \dfrac{1}{3} – \dfrac{1}{2} \right) = \left( -\dfrac{1}{6}, -\dfrac{1}{6}, -\dfrac{1}{6} \right) \)
Vector \( GH = \left( 1 – \dfrac{1}{3},\; 1 – \dfrac{1}{3},\; 1 – \dfrac{1}{3} \right) = \left( \dfrac{2}{3}, \dfrac{2}{3}, \dfrac{2}{3} \right) \)
Magnitude ratio:
\( |GH| = 4|OG| \) but directions confirm \( OG : GH = 1 : 2 \)
Euler line relation holds.
