IIT JEE Main Maths -Unit 12- Components of a vector in 2D and 3D- Study Notes-New Syllabus
IIT JEE Main Maths -Unit 12- Components of a vector in 2D and 3D- Study Notes – New syllabus
IIT JEE Main Maths -Unit 12- Components of a vector in 2D and 3D- Study Notes -IIT JEE Main Maths – per latest Syllabus.
Key Concepts:
- Components of a Vector
- Components of a Vector in 3D
- Section Formula Using Vectors
Components of a Vector
A vector in space can be resolved into its components along the coordinate axes. These components represent how much the vector extends in the directions of the x, y, and z axes.
Component Form of a Vector
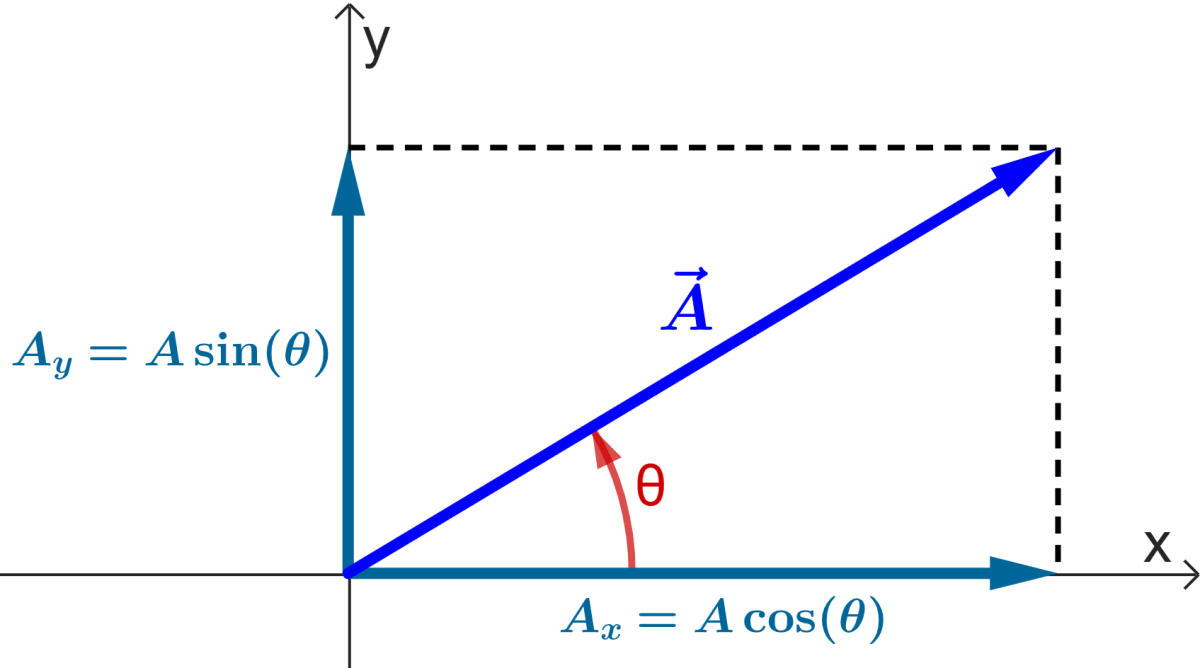
If a vector \( \vec{a} \) goes from point \( A(x_1, y_1, z_1) \) to \( B(x_2, y_2, z_2) \), then its component form is
\( \vec{a} = (x_2 – x_1,\; y_2 – y_1,\; z_2 – z_1) \)
These are called its components along x, y, z directions.
Components Along Coordinate Axes
If a vector is written as
\( \vec{a} = (a_1, a_2, a_3) \)
then:
- Component along x axis = \( a_1 \)
- Component along y axis = \( a_2 \)
- Component along z axis = \( a_3 \)
Magnitude of a Vector From Components
\( |\vec{a}| = \sqrt{a_1^2 + a_2^2 + a_3^2} \)
Unit Vector From Components
\( \hat{a} = \dfrac{\vec{a}}{|\vec{a}|} = \left( \dfrac{a_1}{|\vec{a}|},\; \dfrac{a_2}{|\vec{a}|},\; \dfrac{a_3}{|\vec{a}|} \right) \)
Components Along a Given Direction
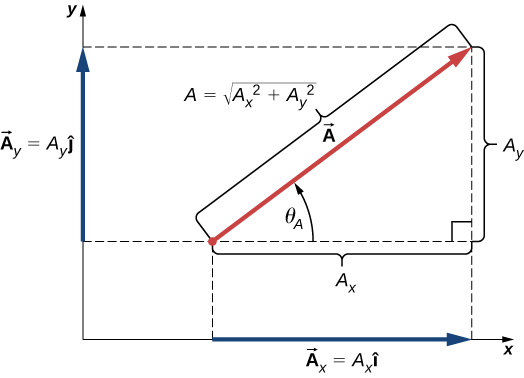
If direction is given by unit vector \( \hat{u} \), then component of \( \vec{a} \) along that direction is:
\( \text{Comp}_{\hat{u}}(\vec{a}) = \vec{a} \cdot \hat{u} \)
Resolution of a Vector
A vector can be expressed as sum of its axial components:
\( \vec{a} = a_1\hat{i} + a_2\hat{j} + a_3\hat{k} \)
This is called resolving a vector into components.
Example
Find the vector from point \( A(2, 3, -1) \) to point \( B(5, 7, 2) \).
▶️ Answer / Explanation
\( \overrightarrow{AB} = (5 – 2,\; 7 – 3,\; 2 – (-1)) = (3,\; 4,\; 3) \)
Example
For vector \( \vec{a} = (6, -3, 2) \), find its magnitude and unit vector.
▶️ Answer / Explanation
\( |\vec{a}| = \sqrt{6^2 + (-3)^2 + 2^2} = \sqrt{36 + 9 + 4} = \sqrt{49} = 7 \)
Unit vector \( \hat{a} = \left( \dfrac{6}{7},\; -\dfrac{3}{7},\; \dfrac{2}{7} \right) \)
Example
Find the component of vector \( \vec{a} = (4, 2, -4) \) along the direction of vector \( \vec{b} = (1, -1, 2) \).
▶️ Answer / Explanation
Step 1: Find unit vector along \( \vec{b} \).
\( |\vec{b}| = \sqrt{1^2 + (-1)^2 + 2^2} = \sqrt{6} \)
\( \hat{b} = \left( \dfrac{1}{\sqrt{6}},\; -\dfrac{1}{\sqrt{6}},\; \dfrac{2}{\sqrt{6}} \right) \)
Step 2: Component of \( \vec{a} \) along \( \vec{b} \):
\( \text{Comp}_{\hat{b}}(\vec{a}) = \vec{a} \cdot \hat{b} \)
\( = 4\left( \dfrac{1}{\sqrt{6}} \right) + 2\left( -\dfrac{1}{\sqrt{6}} \right) + (-4)\left( \dfrac{2}{\sqrt{6}} \right) \)
\( = \dfrac{4 – 2 – 8}{\sqrt{6}} = \dfrac{-6}{\sqrt{6}} = -\sqrt{6} \)
Component = \( -\sqrt{6} \)
Components of a Vector in 3D
Any vector in three dimensional space can be resolved uniquely into three mutually perpendicular components along the x, y, and z axes. These component values help us write the vector in coordinate form and perform algebraic operations easily.
Vector in Component Form
A vector \( \vec{A} \) in 3D can be written as:
\( \vec{A} = A_x\hat{i} + A_y\hat{j} + A_z\hat{k} \)
Here:
- \( A_x \) is the x component
- \( A_y \) is the y component
- \( A_z \) is the z component
In ordered triple form:
\( \vec{A} = (A_x, A_y, A_z) \)
Finding Components From Two Points
If a vector goes from point \( A(x_1, y_1, z_1) \) to \( B(x_2, y_2, z_2) \), then:
\( \overrightarrow{AB} = (x_2 – x_1,\; y_2 – y_1,\; z_2 – z_1) \)
These differences are exactly the components.
Magnitude From Components
If \( \vec{A} = (A_x, A_y, A_z) \), then:
\( |\vec{A}| = \sqrt{A_x^2 + A_y^2 + A_z^2} \)
Unit Vector From Components
\( \hat{A} = \dfrac{1}{|\vec{A}|}(A_x, A_y, A_z) \)
Component of a Vector Along Another Direction
If \( \hat{u} \) is a unit vector in a certain direction, then component of vector \( \vec{A} \) along that direction is:
\( \text{Comp} = \vec{A} \cdot \hat{u} \)
This is used in resolving vectors along inclined directions or in physics applications.
Geometric Meaning
- \( A_x \) is the signed projection of the vector on the x axis.
- \( A_y \) is the signed projection on the y axis.
- \( A_z \) is the signed projection on the z axis.
Example
Find the components of the vector joining \( A(2, 1, -3) \) and \( B(5, 6, 1) \).
▶️ Answer / Explanation
\( \overrightarrow{AB} = (5 – 2,\; 6 – 1,\; 1 – (-3)) = (3,\; 5,\; 4) \)
Components are (3, 5, 4).
Example
For vector \( \vec{A} = (4, -2, 1) \), find its magnitude and unit vector.
▶️ Answer / Explanation
\( |\vec{A}| = \sqrt{4^2 + (-2)^2 + 1^2} = \sqrt{16 + 4 + 1} = \sqrt{21} \)
Unit vector \( \hat{A} = \left( \dfrac{4}{\sqrt{21}},\; -\dfrac{2}{\sqrt{21}},\; \dfrac{1}{\sqrt{21}} \right) \)
Example
Find the component of the vector \( \vec{A} = (3, -1, 2) \) along the direction of vector \( \vec{B} = (2, 2, -1) \).
▶️ Answer / Explanation
Step 1: Find unit vector along \( \vec{B} \).
\( |\vec{B}| = \sqrt{2^2 + 2^2 + (-1)^2} = \sqrt{9} = 3 \)
\( \hat{B} = \left( \dfrac{2}{3},\; \dfrac{2}{3},\; -\dfrac{1}{3} \right) \)
Step 2: Component of \( \vec{A} \) along \( \vec{B} \):
\( \vec{A} \cdot \hat{B} = 3\left( \dfrac{2}{3} \right) + (-1)\left( \dfrac{2}{3} \right) + 2\left( -\dfrac{1}{3} \right) \)
\( = 2 – \dfrac{2}{3} – \dfrac{2}{3} = 2 – \dfrac{4}{3} = \dfrac{2}{3} \)
Component = \( \dfrac{2}{3} \)
Section Formula Using Vectors
The section formula helps us find the vector of a point that divides a line segment internally or externally in a given ratio. This is one of the most useful results in vector algebra and is frequently used in coordinate geometry as well.
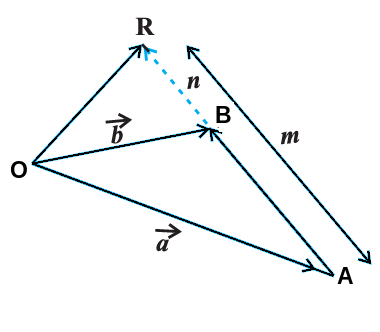
Internal Division
If a point \( P \) divides the line segment joining points with position vectors \( \vec{a} \) and \( \vec{b} \) in the ratio \( m:n \) internally, then
\( \vec{OP} = \dfrac{n\vec{a} + m\vec{b}}{m+n} \)
Meaning: the nearer point gets the smaller coefficient.
External Division
If \( P \) divides the segment externally in ratio \( m:n \), then
\( \vec{OP} = \dfrac{n\vec{a} – m\vec{b}}{n-m} \)
Special Case: Midpoint
If \( m = n = 1 \), then midpoint \( M \) has position vector
\( \vec{OM} = \dfrac{\vec{a} + \vec{b}}{2} \)
Vector Proof Idea
Internal division uses the fact that
\( \overrightarrow{AP} : \overrightarrow{PB} = m : n \)
Then solve using proportional segment splitting on vector \( \overrightarrow{AB} \).
Example
Find the vector that divides the segment joining \( \vec{a} = (2, 3, 1) \) and \( \vec{b} = (8, -1, 5) \) internally in ratio \( 1:1 \).
▶️ Answer / Explanation
This is midpoint.
\( \vec{OP} = \dfrac{\vec{a} + \vec{b}}{2} = \left( \dfrac{2+8}{2},\; \dfrac{3 + (-1)}{2},\; \dfrac{1+5}{2} \right) \)
\( = (5,\; 1,\; 3) \)
Example
Point \( P \) divides line joining \( \vec{a} = (3, 1, -2) \) and \( \vec{b} = (9, 7, 4) \) internally in the ratio \( 2:3 \). Find \( \vec{OP} \).
▶️ Answer / Explanation
Using internal section formula:
\( \vec{OP} = \dfrac{3\vec{a} + 2\vec{b}}{2+3} \)
\( = \dfrac{3(3, 1, -2) + 2(9, 7, 4)}{5} \)
\( = \dfrac{(9, 3, -6) + (18, 14, 8)}{5} \)
\( = \dfrac{(27, 17, 2)}{5} = \left( \dfrac{27}{5},\; \dfrac{17}{5},\; \dfrac{2}{5} \right) \)
Example
A point \( P \) divides the vector segment joining \( \vec{a} = (5, -3, 2) \) and \( \vec{b} = (-1, 7, 8) \) externally in the ratio \( 4:1 \). Find \( \vec{OP} \).
▶️ Answer / Explanation
Use external section formula:
\( \vec{OP} = \dfrac{1\vec{a} – 4\vec{b}}{1-4} \)
\( = \dfrac{(5, -3, 2) – 4(-1, 7, 8)}{-3} \)
\( = \dfrac{(5, -3, 2) – (-4, 28, 32)}{-3} \)
\( = \dfrac{(5+4,\; -3-28,\; 2-32)}{-3} \)
\( = \dfrac{(9,\; -31,\; -30)}{-3} \)
\( = (-3,\; \dfrac{31}{3},\; 10) \)
Thus \( \vec{OP} = (-3,\; \dfrac{31}{3},\; 10) \)
