IIT JEE Main Maths -Unit 12- Vector (cross) product- Study Notes-New Syllabus
IIT JEE Main Maths -Unit 12- Vector (cross) product – Study Notes – New syllabus
IIT JEE Main Maths -Unit 12- Vector (cross) product – Study Notes -IIT JEE Main Maths – per latest Syllabus.
Key Concepts:
- Cross Product (Vector Product)
- Properties of Vector (Cross) Product
Cross Product (Vector Product)
The cross product of two vectors is a vector that is perpendicular to both the given vectors. It is extremely important in 3D geometry, physics, torque, moment, area, and determining direction of perpendicular.
If \( \vec{a} = (a_1, a_2, a_3) \) and \( \vec{b} = (b_1, b_2, b_3) \), then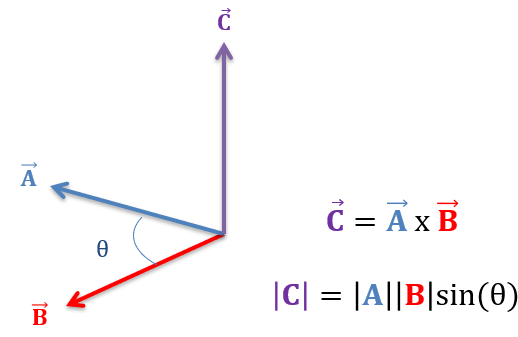
\( \vec{a} \times \vec{b} = \begin{vmatrix} \hat{i} & \hat{j} & \hat{k} \\ a_1 & a_2 & a_3 \\ b_1 & b_2 & b_3 \end{vmatrix} \)
Formula for Cross Product
\( \vec{a} \times \vec{b} = \left( a_2b_3 – a_3b_2,\; a_3b_1 – a_1b_3,\; a_1b_2 – a_2b_1 \right) \)
Magnitude of Cross Product
\( |\vec{a} \times \vec{b}| = |\vec{a}|\,|\vec{b}|\sin\theta \)
- It gives area of parallelogram formed by vectors \( \vec{a} \) and \( \vec{b} \).
- Half of this gives area of triangle.
Direction of Cross Product
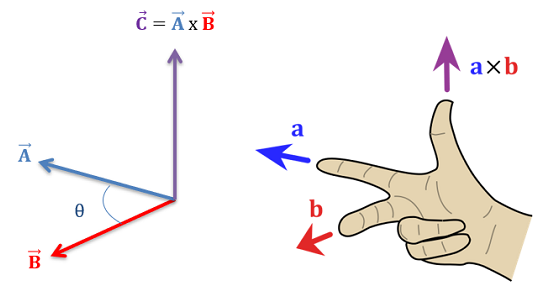
- Direction is perpendicular to both vectors.
- Direction is given by right hand rule.
Important Properties
- \( \vec{a} \times \vec{b} = -(\vec{b} \times \vec{a}) \)
- \( \vec{a} \times \vec{a} = \vec{0} \)
- Distributive: \( \vec{a} \times (\vec{b} + \vec{c}) = \vec{a} \times \vec{b} + \vec{a} \times \vec{c} \)
- Not associative
Condition for Parallel Vectors
\( \vec{a} \times \vec{b} = \vec{0} \quad \text{if and only if vectors are parallel} \)
Geometric Interpretation
- Magnitude gives area of parallelogram.
- Direction is perpendicular normal to the plane of vectors.
Example
Find \( \vec{a} \times \vec{b} \), where \( \vec{a} = (1, 2, 3) \) and \( \vec{b} = (2, -1, 1) \).
▶️ Answer / Explanation
\( \vec{a} \times \vec{b} = \begin{vmatrix} \hat{i} & \hat{j} & \hat{k} \\ 1 & 2 & 3 \\ 2 & -1 & 1 \end{vmatrix} \)
\( = \hat{i}(2\cdot1 – 3(-1)) – \hat{j}(1\cdot1 – 3\cdot2) + \hat{k}(1(-1) – 2\cdot2) \)
\( = \hat{i}(2 + 3) – \hat{j}(1 – 6) + \hat{k}(-1 – 4) \)
\( = (5, 5, -5) \)
Result: \( (5, 5, -5) \)
Example
Find the area of the triangle whose vertices have position vectors \( \vec{A} = (1, 0, 2) \), \( \vec{B} = (3, -1, 4) \), \( \vec{C} = (2, 1, 0) \).
▶️ Answer / Explanation
Step 1: Compute vectors
\( \overrightarrow{AB} = (2, -1, 2) \)
\( \overrightarrow{AC} = (1, 1, -2) \)
Step 2: Cross product
\( \overrightarrow{AB} \times \overrightarrow{AC} = \begin{vmatrix} \hat{i} & \hat{j} & \hat{k} \\ 2 & -1 & 2 \\ 1 & 1 & -2 \end{vmatrix} \)
\( = \hat{i}((-1)(-2) – 2\cdot1) – \hat{j}(2(-2) – 2\cdot1) + \hat{k}(2\cdot1 – (-1)1) \)
\( = \hat{i}(2 – 2) – \hat{j}(-4 – 2) + \hat{k}(2 + 1) \)
\( = (0, 6, 3) \)
Step 3: Area of triangle
Area \( = \dfrac{1}{2}|\overrightarrow{AB} \times \overrightarrow{AC}| = \dfrac{1}{2}\sqrt{0^2 + 6^2 + 3^2} \)
\( = \dfrac{1}{2}\sqrt{36 + 9} = \dfrac{\sqrt{45}}{2} = \dfrac{3\sqrt{5}}{2} \)
Area = \( \dfrac{3\sqrt{5}}{2} \)
Example
Show that vectors \( \vec{a} = (2, -1, 3) \), \( \vec{b} = (1, 4, -2) \), and \( \vec{c} = (3, 3, 1) \) are coplanar using cross product.
▶️ Answer / Explanation
Vectors are coplanar if
\( \vec{c} \cdot (\vec{a} \times \vec{b}) = 0 \)
Step 1: Compute \( \vec{a} \times \vec{b} \)
\( \vec{a} \times \vec{b} = \begin{vmatrix} \hat{i} & \hat{j} & \hat{k} \\ 2 & -1 & 3 \\ 1 & 4 & -2 \end{vmatrix} \)
\( = \hat{i}((-1)(-2) – 3\cdot4) – \hat{j}(2(-2) – 3\cdot1) + \hat{k}(2\cdot4 – (-1)1) \)
\( = (2 – 12,\; -(-4 – 3),\; 8 + 1) \)
\( = (-10, 7, 9) \)
Step 2: Triple product with \( \vec{c} \)
\( \vec{c} \cdot (\vec{a} \times \vec{b}) = (3)(-10) + (3)(7) + (1)(9) \)
\( = -30 + 21 + 9 = 0 \)
Thus vectors are coplanar.
Properties of Vector (Cross) Product
The vector cross product of two vectors gives another vector that is perpendicular to both. It is widely used in JEE for finding area, normal vectors, torque, vector identities and geometry.
If \( \vec{a} = (a_1,a_2,a_3) \), \( \vec{b} = (b_1,b_2,b_3) \), then
\( \vec{a} \times \vec{b} = \begin{vmatrix} \hat{i} & \hat{j} & \hat{k} \\ a_1 & a_2 & a_3 \\ b_1 & b_2 & b_3 \end{vmatrix} \)
Geometrically,
\( |\vec{a} \times \vec{b}| = |\vec{a}|\,|\vec{b}| \sin\theta \)
Direction is perpendicular to both vectors.
Anti Commutative Property
\( \vec{a} \times \vec{b} = -(\vec{b} \times \vec{a}) \)
- Reversing order changes the sign.
Distributive Property
\( \vec{a} \times (\vec{b} + \vec{c}) = \vec{a} \times \vec{b} + \vec{a} \times \vec{c} \)
- Useful for expanding geometry expressions.
Scalar Multiplication Property
\( (k\vec{a}) \times \vec{b} = k(\vec{a} \times \vec{b}) = \vec{a} \times (k\vec{b}) \)
5. Perpendicularity Property
\( \vec{a} \times \vec{b} \) is perpendicular to both \( \vec{a} \) and \( \vec{b} \)
- Used to find normal vectors to planes.
6. Zero Cross Product Condition
\( \vec{a} \times \vec{b} = \vec{0} \quad \text{if and only if vectors are parallel} \)
Magnitude Property
\( |\vec{a} \times \vec{b}| = |\vec{a}|\,|\vec{b}| \sin\theta \)
- Maximum magnitude when vectors are perpendicular.
Area Interpretation
Area of parallelogram = \( |\vec{a} \times \vec{b}| \)
Area of triangle = \( \dfrac{1}{2}|\vec{a} \times \vec{b}| \)
Cross Product With Itself
\( \vec{a} \times \vec{a} = \vec{0} \)
- Because angle is zero so \( \sin 0 = 0 \).
Cyclic Properties
\( \hat{i} \times \hat{j} = \hat{k} \)
\( \hat{j} \times \hat{k} = \hat{i} \)
\( \hat{k} \times \hat{i} = \hat{j} \)
Reversed order gives negative:
\( \hat{j} \times \hat{i} = -\hat{k} \), etc.
Vector Triple Product Expansion
\( \vec{a} \times (\vec{b} \times \vec{c}) = \vec{b}(\vec{a} \cdot \vec{c}) – \vec{c}(\vec{a} \cdot \vec{b}) \)
- Known as BAC CAB rule.
Scalar Triple Product Relation
\( [\vec{a}\ \vec{b}\ \vec{c}] = \vec{a} \cdot (\vec{b} \times \vec{c}) \)
- Volume of parallelepiped.
Cross Product Is Not Associative
\( \vec{a} \times (\vec{b} \times \vec{c}) \neq (\vec{a} \times \vec{b}) \times \vec{c} \)
Example
Given vectors \( \vec{a} = (2, 1, -1) \) \( \vec{b} = (1, -3, 4) \), compute:
(i) \( \vec{a} \times \vec{b} \)
(ii) Verify that \( \vec{a} \times \vec{b} \) is perpendicular to both vectors.
▶️ Answer / Explanation
(i) Cross product
\( \vec{a} \times \vec{b} = \begin{vmatrix} \hat{i} & \hat{j} & \hat{k} \\ 2 & 1 & -1 \\ 1 & -3 & 4 \end{vmatrix} \)
\( = \hat{i}(1\cdot4 – (-1)(-3)) – \hat{j}(2\cdot4 – (-1)(1)) + \hat{k}(2(-3) – 1(1)) \)
\( = (4 – 3,\; -(8 + 1),\; (-6 – 1)) = (1,\; -9,\; -7) \)
(ii) Perpendicularity check
\( \vec{a} \cdot (\vec{a} \times \vec{b}) = 2(1) + 1(-9) + (-1)(-7) = 2 – 9 + 7 = 0 \)
\( \vec{b} \cdot (\vec{a} \times \vec{b}) = 1(1) + (-3)(-9) + 4(-7) = 1 + 27 – 28 = 0 \)
Since both dot products are zero, cross product is perpendicular to both vectors.
Example
Given \( \vec{a} = (3, -2, 1) \), \( \vec{b} = (1, 0, -1) \), find the area of the triangle formed by these two vectors.
▶️ Answer / Explanation
Step 1: Cross product
\( \vec{a} \times \vec{b} = \begin{vmatrix} \hat{i} & \hat{j} & \hat{k} \\ 3 & -2 & 1 \\ 1 & 0 & -1 \end{vmatrix} \)
\( = \hat{i}((-2)(-1) – 1\cdot0) – \hat{j}(3(-1) – 1\cdot1) + \hat{k}(3\cdot0 – (-2)(1)) \)
\( = (2,\; 4,\; 2) \)
Step 2: Magnitude
\( |\vec{a} \times \vec{b}| = \sqrt{2^2 + 4^2 + 2^2} = \sqrt{24} = 2\sqrt{6} \)
Step 3: Area of triangle
Area \( = \dfrac{1}{2}|\vec{a} \times \vec{b}| = \sqrt{6} \)
Final Answer: \( \sqrt{6} \)
