IIT JEE Main Maths -Unit 12- Vector Triple Product- Study Notes-New Syllabus
IIT JEE Main Maths -Unit 12- Vector Triple Product – Study Notes – New syllabus
IIT JEE Main Maths -Unit 12- Vector Triple Product – Study Notes -IIT JEE Main Maths – per latest Syllabus.
Key Concepts:
- Vector Triple Product
Vector Triple Product
The vector triple product involves the cross product of a vector with another cross product. It appears frequently in JEE in questions related to vector identities, perpendicularity, geometry of lines and planes, and simplifying vector expressions.
The vector triple product is an expression of the form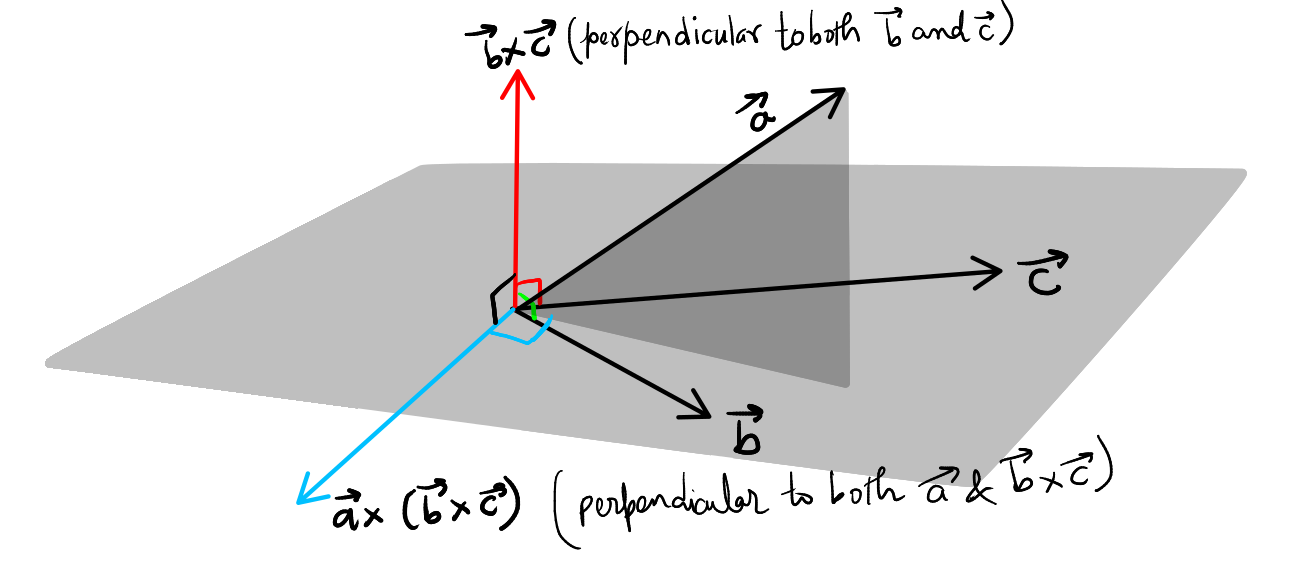
\( \vec{a} \times (\vec{b} \times \vec{c}) \)
This results in a vector.
BAC–CAB Rule (Main Formula)
The most important identity is
\( \vec{a} \times (\vec{b} \times \vec{c}) = \vec{b}(\vec{a} \cdot \vec{c}) – \vec{c}(\vec{a} \cdot \vec{b}) \)
This is known as the BAC–CAB rule and must be memorized for JEE.
Key Observations
- The resulting vector is a linear combination of \( \vec{b} \) and \( \vec{c} \).
- It never contains any component along \( \vec{a} \).
- Order of vectors matters.
Important Result
If we swap vectors in the first cross product:
\( (\vec{a} \times \vec{b}) \times \vec{c} = \vec{b}(\vec{a} \cdot \vec{c}) – \vec{a}(\vec{b} \cdot \vec{c}) \)
Condition for Parallel Vectors
If \( \vec{b} \parallel \vec{c} \), then \( \vec{b} \times \vec{c} = \vec{0} \) and the triple product becomes zero.
Uses in JEE
- Simplifying vector expressions
- Checking perpendicularity
- Finding vector equations of planes
- Proving identities
Example
Simplify \( \vec{a} \times (\vec{b} \times \vec{c}) \) for \( \vec{a} = (1, 2, 3) \), \( \vec{b} = (2, 0, 1) \), \( \vec{c} = (1, -1, 2) \).
▶️ Answer / Explanation
Step 1: Compute dot products
\( \vec{a} \cdot \vec{c} = 1(1) + 2(-1) + 3(2) = 1 – 2 + 6 = 5 \)
\( \vec{a} \cdot \vec{b} = 1(2) + 2(0) + 3(1) = 2 + 0 + 3 = 5 \)
Step 2: Apply BAC–CAB rule
\( \vec{a} \times (\vec{b} \times \vec{c}) = \vec{b}(\vec{a} \cdot \vec{c}) – \vec{c}(\vec{a} \cdot \vec{b}) \)
\( = 5\vec{b} – 5\vec{c} = 5(\vec{b} – \vec{c}) \)
\( = 5[(2, 0, 1) – (1, -1, 2)] = 5(1, 1, -1) = (5, 5, -5) \)
Result: \( (5, 5, -5) \)
Example
Simplify the expression \( (\vec{x} \times \vec{y}) \times \vec{z} \) using the VTP identity.
▶️ Answer / Explanation
Using the identity
\( (\vec{a} \times \vec{b}) \times \vec{c} = \vec{b}(\vec{a} \cdot \vec{c}) – \vec{a}(\vec{b} \cdot \vec{c}) \)
Replace:
- \( \vec{a} = \vec{x} \)
- \( \vec{b} = \vec{y} \)
- \( \vec{c} = \vec{z} \)
So
\( (\vec{x} \times \vec{y}) \times \vec{z} = \vec{y}(\vec{x} \cdot \vec{z}) – \vec{x}(\vec{y} \cdot \vec{z}) \)
Example
Given vectors \( \vec{a} = (2, -1, 3) \), \( \vec{b} = (1, 4, -2) \), \( \vec{c} = (0, 2, 1) \), show that \( \vec{a} \times (\vec{b} \times \vec{c}) \) lies in the plane containing vectors \( \vec{b} \) and \( \vec{c} \).
▶️ Answer / Explanation
Using BAC–CAB rule:
\( \vec{a} \times (\vec{b} \times \vec{c}) = \vec{b}(\vec{a} \cdot \vec{c}) – \vec{c}(\vec{a} \cdot \vec{b}) \)
Step 1: Compute necessary dot products
\( \vec{a} \cdot \vec{c} = 2(0) + (-1)(2) + 3(1) = -2 + 3 = 1 \)
\( \vec{a} \cdot \vec{b} = 2(1) + (-1)(4) + 3(-2) = 2 – 4 – 6 = -8 \)
Step 2: Substitute
\( \vec{a} \times (\vec{b} \times \vec{c}) = 1\vec{b} – (-8)\vec{c} = \vec{b} + 8\vec{c} \)
Step 3: Interpretation
The expression is a linear combination of \( \vec{b} \) and \( \vec{c} \).
So the result vector lies in the plane spanned by \( \vec{b} \) and \( \vec{c} \).
Hence proved.
