IIT JEE Main Maths -Unit 13- Addition and multiplication theorems- Study Notes-New Syllabus

Addition and Multiplication Theorems of Probability

These two theorems are the foundation of probability. Nearly every JEE probability problem uses these formulas.

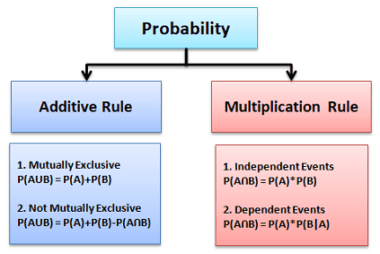
Addition Theorem of Probability

(a) For Mutually Exclusive Events

If two events cannot occur together (like getting 2 or 5 on a die):

\( P(A \cup B) = P(A) + P(B) \)

Because

\( P(A \cap B) = 0 \)

(b) General Addition Rule (Events may occur together)

\( P(A \cup B) = P(A) + P(B) – P(A \cap B) \)

This is the most frequently used rule in JEE.

(c) Extension to Three Events

\( P(A \cup B \cup C) = P(A) + P(B) + P(C)\newline – P(A \cap B) – P(B \cap C) – P(C \cap A) + P(A \cap B \cap C) \)

Multiplication Theorem of Probability

The multiplication theorem connects intersection of events with independence or conditional probability.

(a) General Multiplication Theorem

For any two events:

\( P(A \cap B) = P(A)\cdot P(B|A) \)

And also:

\( P(A \cap B) = P(B)\cdot P(A|B) \)

(b) Independent Events

Two events are independent if occurrence of one does not affect the other.

\( P(A \cap B) = P(A)P(B) \)

This special case is used heavily in JEE.

(c) Extension to Three Independent Events

\( P(A \cap B \cap C) = P(A)P(B)P(C) \)

Valid only when all three are mutually independent.

Useful Identities

• \( P(A \cup B)’ = P(A’ \cap B’) \)
• \( P(A \cap B)’ = P(A’ \cup B’) \)
• \( P(A \cup B) = 1 – P(A’ \cap B’) \)
• \( P(\text{none}) = 1 – P(\text{at least one}) \)