IIT JEE Main Maths -Unit 13- Bayes’ theorem- Study Notes-New Syllabus
IIT JEE Main Maths -Unit 13- Bayes’ theorem – Study Notes – New syllabus
IIT JEE Main Maths -Unit 13- Bayes’ theorem – Study Notes -IIT JEE Main Maths – per latest Syllabus.
Key Concepts:
- Bayes Theorem
Bayes Theorem
Bayes theorem gives the probability of an event based on updated or conditional information. It is heavily used in JEE when a problem involves multiple causes for an event and we need the probability of one specific cause.
Conditional Probability Revision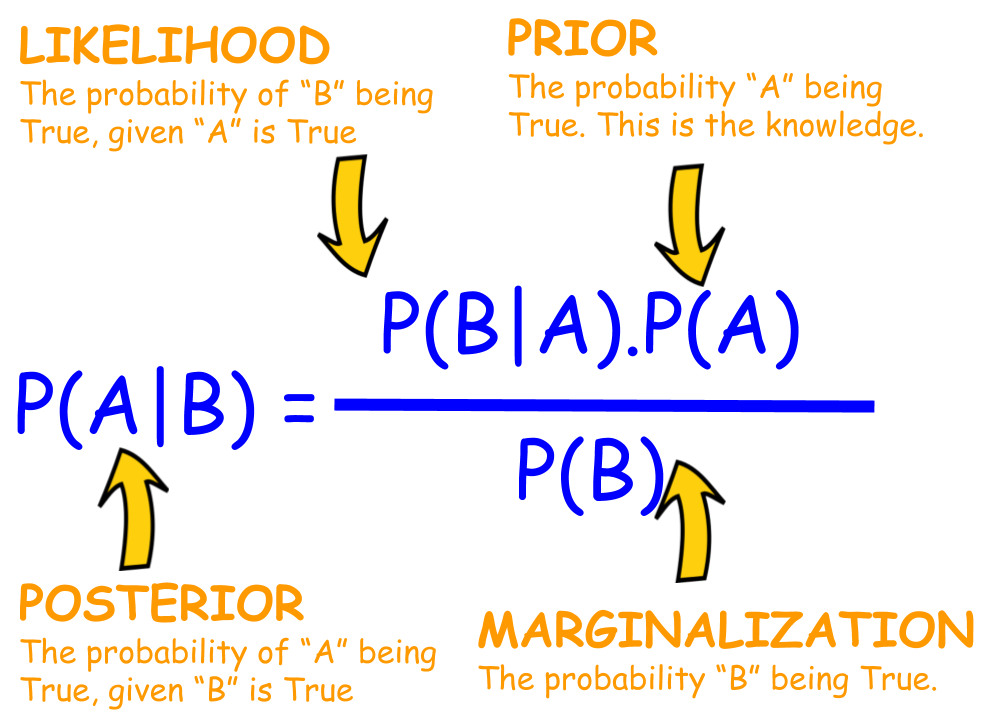
\( P(A|B) = \dfrac{P(A \cap B)}{P(B)} \)
This is the foundation of Bayes theorem.
Partition of the Sample Space
Suppose \( B_1, B_2, \dots, B_n \) are mutually exclusive events that cover all possibilities. Then for any event \( A \):
\( P(A) = \sum_{i=1}^n P(B_i)P(A|B_i) \)
This is used to compute the total probability of A.
Bayes Theorem (Most Important Formula)
Bayes theorem finds the probability of event \( B_k \) when event \( A \) has already occurred.
\( P(B_k|A) = \dfrac{P(B_k)P(A|B_k)}{\sum\limits_{i=1}^n P(B_i)P(A|B_i)} \)
Meaning of Bayes Theorem
Bayes theorem answers: Given that the effect (event A) has occurred, what is the probability that a particular cause \( B_k \) produced it?
Examples:
- Defective item from a particular machine
- Incorrect answer from a student of a certain class
- Positive test coming from infected vs non-infected person
When to Use Bayes Theorem
- Multiple sources
- Different probabilities of selection
- Given the final result
- You need to find the most likely source/event
Example
A box contains 3 red and 2 green balls. One ball is drawn and it is found to be red. What is the probability that it was one of the first three red balls?
▶️ Answer / Explanation
Let \( B_1 \) = selected ball is from the 3 red ones. Let \( A \) = selected ball is red.
\( P(B_1) = \dfrac{3}{5} \)
Given drawing from \( B_1 \) always gives red, so \( P(A|B_1) = 1 \)
Total probability of red: \( P(A) = \dfrac{3}{5} \)
Bayes: \( P(B_1|A) = \dfrac{P(B_1)P(A|B_1)}{P(A)} = \dfrac{\frac{3}{5}}{\frac{3}{5}} = 1 \)
Answer: 1
Example
Machine A produces 40 percent items, Machine B produces 60 percent items. Defective rate: A → 3 percent B → 5 percent If an item is found defective, find the probability that it was produced by Machine A.
▶️ Answer / Explanation
Let \( B_1 = \) item from Machine A \( B_2 = \) item from Machine B \( A = \) item is defective
\( P(B_1) = 0.4,\ P(B_2) = 0.6 \)
\( P(A|B_1) = 0.03 \) \( P(A|B_2) = 0.05 \)
Total defective probability:
\( P(A) = 0.4(0.03) + 0.6(0.05) = 0.012 + 0.03 = 0.042 \)
Using Bayes:
\( P(B_1|A) = \dfrac{0.4(0.03)}{0.042} = \dfrac{0.012}{0.042} = \dfrac{2}{7} \)
Answer: \( \dfrac{2}{7} \)
Example
A student appears for an exam from three institutes A, B, and C. Probability of choosing institute: A = 0.3, B = 0.4, C = 0.3 Success probabilities: A = 0.7, B = 0.5, C = 0.9 If a student is selected, find the probability that he is from institute C.
▶️ Answer / Explanation
Let \( B_1,B_2,B_3 \) = choosing A, B, C Let \( A = \) student is selected
Total success probability:
\( P(A) = 0.3(0.7) + 0.4(0.5) + 0.3(0.9) \)
\( = 0.21 + 0.20 + 0.27 = 0.68 \)
Using Bayes:
\( P(C|A) = \dfrac{0.3(0.9)}{0.68} = \dfrac{0.27}{0.68} \)
\( = 0.397 \approx 0.40 \)
Answer: approximately 0.40
