IIT JEE Main Maths -Unit 13- Probability distribution of random variables- Study Notes-New Syllabus
IIT JEE Main Maths -Unit 13- Probability distribution of random variables- Study Notes – New syllabus
IIT JEE Main Maths -Unit 13- Probability distribution of random variables- Study Notes -IIT JEE Main Maths – per latest Syllabus.
Key Concepts:
- Random Variables and Expectation
- Binomial Distribution
- Mean and Variance of a Binomial Distribution
Random Variables and Expectation
Random variables and expectation are the foundation of probability for JEE questions involving coins, dice, probability distributions, and discrete outcomes.
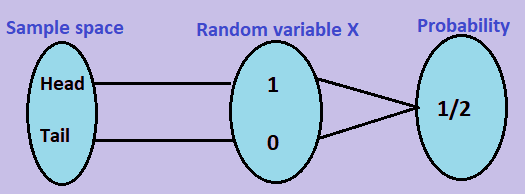
Random Variable (R.V.)
A random variable is a variable whose value depends on the outcome of a random experiment.
Definition:
A random variable \( X \) is a function that assigns a real number to each outcome of a sample space.
Types of Random Variables
- Discrete R.V. Takes finite or countably infinite values. Examples: number of heads, number on a die.
- Continuous R.V. Takes infinitely many values in an interval. (Not required for JEE Main)
JEE focuses ONLY on discrete random variables.
Probability Distribution of a Discrete R.V.
A probability distribution assigns probability to every possible value of \( X \).
Conditions:
- \( P(X = x_i) \ge 0 \)
- \( \sum P(X = x_i) = 1 \)
Expectation / Expected Value (Mean)
Expectation is the long-run average value of the random variable.
Formula for Discrete R.V.:
\( E(X) = \sum x_i P(X = x_i) \)
Expectation = weighted average of all possible values.
Expectation of a Function of Random Variable
If \( Y = g(X) \), then:
\( E[g(X)] = \sum g(x_i)P(X = x_i) \)
Used frequently for questions on \( X^2 \), profit, loss, etc.
Properties of Expectation (Very Important for JEE)
- \( E(aX + b) = aE(X) + b \)
- \( E(X + Y) = E(X) + E(Y) \)
- If X, Y independent → still additive
- \( E(c) = c \) for constant c
Variance of R.V. (Brief)
\( Var(X) = E(X^2) – [E(X)]^2 \)
Useful when combined with expectation problems.
Examples
Example
A coin is tossed. Define a random variable \( X \) such that: Head → 1, Tail → 0. Find \( E(X) \).
▶️ Answer / Explanation
\( P(X=1) = \dfrac{1}{2},\ \ P(X=0) = \dfrac{1}{2} \)
\( E(X) = 1\left(\dfrac{1}{2}\right) + 0\left(\dfrac{1}{2}\right) = \dfrac{1}{2} \)
Answer: \( E(X) = \dfrac{1}{2} \)
Example
A die is rolled. Let the random variable \( X \) denote the number appearing on the die. Find \( E(X) \).
▶️ Answer / Explanation
Possible values: 1, 2, 3, 4, 5, 6 Each with probability \( \dfrac{1}{6} \).
\( E(X) = \dfrac{1}{6}(1 + 2 + 3 + 4 + 5 + 6) \)
\( = \dfrac{21}{6} = 3.5 \)
Answer: \( 3.5 \)
Example
A game involves drawing one card. If you draw: Red card → gain 4 points Black card → lose 2 points Find the expected gain.
▶️ Answer / Explanation
Total cards = 52 Red = 26, Black = 26
Let X = gain. \( X = 4 \) with probability \( \dfrac{1}{2} \) \( X = -2 \) with probability \( \dfrac{1}{2} \)
\( E(X) = 4\left(\dfrac{1}{2}\right) + (-2)\left(\dfrac{1}{2}\right) \)
\( = 2 – 1 = 1 \)
Answer: Expected gain = 1 point
Binomial Distribution
Binomial distribution gives the probability of getting exactly \( k \) successes in \( n \) independent Bernoulli trials (like coin tosses, dice outcomes, questions attempted, etc.)

Bernoulli Trial
A trial is called a Bernoulli trial if:
- Only two outcomes: success or failure
- Probability of success = \( p \)
- Probability of failure = \( q = 1 – p \)
- Trials are independent
- Number of trials = \( n \)
Binomial Distribution Definition
If a random variable \( X \) denotes the number of successes in \( n \) independent Bernoulli trials, then:
\( X \sim B(n, p) \)
- \( n \) = number of trials
- \( p \) = probability of success
- \( q = 1 – p \) = probability of failure
Probability Mass Function (PMF)
The probability of getting exactly \( k \) successes:
\( P(X = k) = {n \choose k}p^k q^{\,n-k} \)
Where:
- \( {n \choose k} = \dfrac{n!}{k!(n-k)!} \)
- \( k = 0, 1, 2, \dots, n \)
Mean and Variance of Binomial Distribution
Mean: \( E(X) = np \)
Variance: \( Var(X) = npq \)
Standard Deviation: \( \sigma = \sqrt{npq} \)
Important Properties
- \( P(X = 0) = q^n \)
- \( P(X = n) = p^n \)
- Maximum term occurs at \( k = (n+1)p \) (largest integer)
- Distribution becomes symmetric if \( p = q = \dfrac{1}{2} \)
- For large \( n \), binomial approximates normal (not needed for JEE Main)
Conditions for Using Binomial Distribution (JEE Important)
- Finite number of trials \( n \)
- Independent trials
- Two outcomes per trial
- Probability of success remains constant
Example
A fair coin is tossed 5 times. What is the probability of getting exactly 3 heads?
▶️ Answer / Explanation
Here, \( n = 5,\ p = \dfrac{1}{2},\ q = \dfrac{1}{2},\ k = 3 \)
\( P(X = 3) = {5 \choose 3}\left(\dfrac{1}{2}\right)^3\left(\dfrac{1}{2}\right)^2 \)
\( = 10\left(\dfrac{1}{32}\right) = \dfrac{10}{32} = \dfrac{5}{16} \)
Answer: \( \dfrac{5}{16} \)
Example
The probability that a student solves a problem is \( 0.3 \). If he attempts 10 problems, find the probability that he solves exactly 4 problems.
▶️ Answer / Explanation
\( n = 10,\ p = 0.3,\ q = 0.7,\ k = 4 \)
\( P(X = 4) = {10 \choose 4}(0.3)^4(0.7)^6 \)
\( = 210 \times 0.0081 \times 0.117649 \)
\( = 210 \times 0.000952 \approx 0.200 \)
Answer: approximately 0.20
Example
A die is rolled 8 times. Find the probability of getting at most 2 sixes.
▶️ Answer / Explanation
Success = getting a 6 → \( p = \dfrac{1}{6} \), Failure → \( q = \dfrac{5}{6} \)
Required: \( P(X \le 2) = P(X=0) + P(X=1) + P(X=2) \)
Term 1: \( X=0 \)
\( {8 \choose 0}(p)^0(q)^8 = \left(\dfrac{5}{6}\right)^8 \)
Term 2: \( X=1 \)
\( {8 \choose 1}(p)^1(q)^7 = 8\left(\dfrac{1}{6}\right)\left(\dfrac{5}{6}\right)^7 \)
Term 3: \( X=2 \)
\( {8 \choose 2}(p)^2(q)^6 = 28\left(\dfrac{1}{36}\right)\left(\dfrac{5}{6}\right)^6 \)
Add all three terms (calculator not required in JEE pattern).
Final Answer:
\( P(X \le 2) = \left(\dfrac{5}{6}\right)^8 + 8\left(\dfrac{1}{6}\right)\left(\dfrac{5}{6}\right)^7 + 28\left(\dfrac{1}{36}\right)\left(\dfrac{5}{6}\right)^6 \)
(Can be left in this form in exams.)
Mean and Variance of a Binomial Distribution
If \( X \) is a binomial random variable with parameters \( n \) (number of trials) and \( p \) (probability of success), then:
\( X \sim B(n,p) \)
Mean of Binomial Distribution
The mean (expected value) of \( X \) is:
\( E(X) = np \)
This represents the average number of successes expected in n trials.
Variance of Binomial Distribution
The variance of \( X \) is:
\( \text{Var}(X) = npq \)
Where:
- \( p = \) probability of success
- \( q = 1-p = \) probability of failure
Standard Deviation
\( \sigma = \sqrt{npq} \)
Derivation (short JEE style) Mean Derivation
\( X \) = number of successes Let indicator variables:
\( X = X_1 + X_2 + … + X_n \)
Where each \( X_i = 1 \) if success in i-th trial, else 0.
\( E(X) = E(X_1) + E(X_2) + … + E(X_n) \)
Since \( E(X_i) = p \), \( E(X) = np \)
Variance Derivation
\( Var(X) = E(X^2) – [E(X)]^2 \)
Using properties of indicator variables and independence:
\( Var(X) = npq \)
(This derivation is sufficient for JEE Main.)
Important JEE Notes
- Mean and variance depend only on n and p.
- If \( p = 0.5 \), binomial distribution is symmetric.
- If variance = mean → \( npq = np \) → \( q = 1 \) → impossible unless p = 0.
- If SD increases, either n or p or both increase.
Example
A coin is tossed 10 times. Find the mean number of heads.
▶️ Answer / Explanation
Here: \( n = 10 \), \( p = \dfrac{1}{2} \)
Mean = \( np = 10 \cdot \dfrac{1}{2} = 5 \)
Answer: 5
Example
For a binomial distribution \( X \sim B(12, 0.25) \), find its mean and variance.
▶️ Answer / Explanation
Mean = \( np = 12 \cdot 0.25 = 3 \)
Variance = \( npq = 12(0.25)(0.75) = 2.25 \)
Answer: Mean = 3, Variance = 2.25
Example
A binomial distribution has mean 8 and variance 6. Find n and p.
▶️ Answer / Explanation
Given:
- \( np = 8 \)
- \( npq = 6 \)
Divide second by first:
\( q = \dfrac{6}{8} = \dfrac{3}{4} \)
Thus \( p = 1 – q = 1 – \dfrac{3}{4} = \dfrac{1}{4} \)
Substitute in \( np = 8 \):
\( n \cdot \dfrac{1}{4} = 8 \Rightarrow n = 32 \)
Answer: \( n = 32,\ p = \dfrac{1}{4} \)
