IIT JEE Main Maths -Unit 14- Basic Trigonometric Definitions and Ratios- Study Notes-New Syllabus
IIT JEE Main Maths -Unit 14- Basic Trigonometric Definitions and Ratios – Study Notes – New syllabus
IIT JEE Main Maths -Unit 14- Basic Trigonometric Definitions and Ratios – Study Notes -IIT JEE Main Maths – per latest Syllabus.
Key Concepts:
- Basic Trigonometric Definitions and Ratios
- Trigonometric Standard Angles
Basic Trigonometric Definitions and Ratios
Trigonometry begins with defining six fundamental ratios based on a right angled triangle. These ratios relate the angles of a triangle to the lengths of its sides. These definitions form the foundation for all advanced trigonometry used in JEE.
Reference Triangle
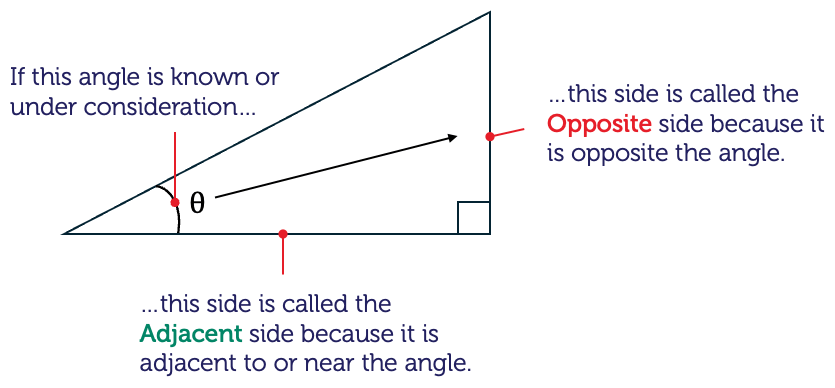
Consider a right angled triangle with angle \( \theta \) and the sides relative to \( \theta \):
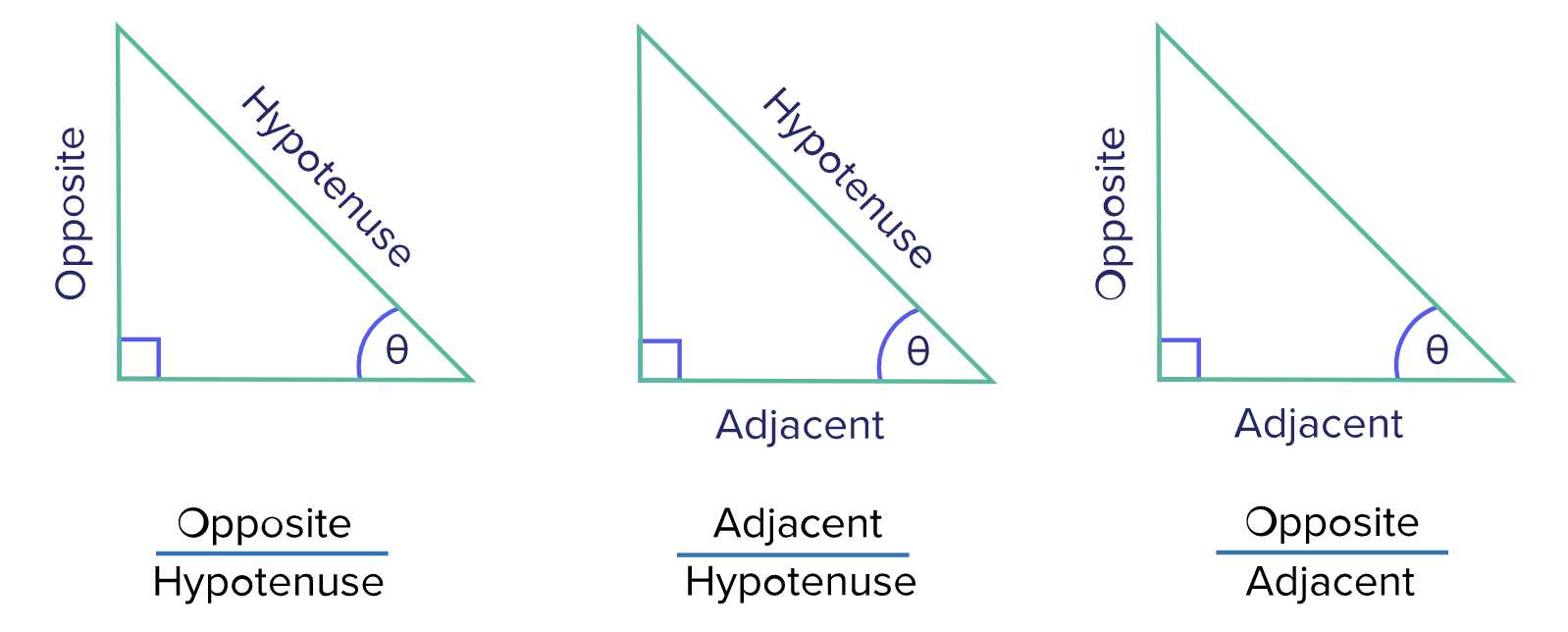
Six Trigonometric Ratios
The six trigonometric ratios for angle \( \theta \) are:
| Ratio | Definition |
| \( \sin\theta \) | \( \dfrac{\text{Perpendicular}}{\text{Hypotenuse}} \) |
| \( \cos\theta \) | \( \dfrac{\text{Base}}{\text{Hypotenuse}} \) |
| \( \tan\theta \) | \( \dfrac{\text{Perpendicular}}{\text{Base}} \) |
| \( \cot\theta \) | \( \dfrac{\text{Base}}{\text{Perpendicular}} \) |
| \( \sec\theta \) | \( \dfrac{\text{Hypotenuse}}{\text{Base}} \) |
| \( \csc\theta \) | \( \dfrac{\text{Hypotenuse}}{\text{Perpendicular}} \) |
Reciprocal Relations
\( \sin\theta = \dfrac{1}{\csc\theta} \), \( \cos\theta = \dfrac{1}{\sec\theta} \), \( \tan\theta = \dfrac{1}{\cot\theta} \)
Quotient Relations
\( \tan\theta = \dfrac{\sin\theta}{\cos\theta} \), \( \cot\theta = \dfrac{\cos\theta}{\sin\theta} \)
Pythagorean Identity
\( \sin^2\theta + \cos^2\theta = 1 \)
Derived formulas:
\( 1 + \tan^2\theta = \sec^2\theta \)
\( 1 + \cot^2\theta = \csc^2\theta \)
Trigonometric Values for Standard Angles
The most commonly used exact values are:
| \( \theta \) | \( \sin\theta \) | \( \cos\theta \) | \( \tan\theta \) |
| \( 0^\circ \) | 0 | 1 | 0 |
| \( 30^\circ \) | \( \dfrac{1}{2} \) | \( \dfrac{\sqrt{3}}{2} \) | \( \dfrac{1}{\sqrt{3}} \) |
| \( 45^\circ \) | \( \dfrac{1}{\sqrt{2}} \) | \( \dfrac{1}{\sqrt{2}} \) | 1 |
| \( 60^\circ \) | \( \dfrac{\sqrt{3}}{2} \) | \( \dfrac{1}{2} \) | \( \sqrt{3} \) |
| \( 90^\circ \) | 1 | 0 | Not defined |
Example
In a right triangle, if \( \sin\theta = \dfrac{3}{5} \), find \( \cos\theta \).
▶️ Answer / Explanation
Given:
\( \sin\theta = \dfrac{3}{5} = \dfrac{P}{H} \Rightarrow P = 3,\ H = 5 \)
Using Pythagoras:
\( B = \sqrt{H^2 – P^2} = \sqrt{25 – 9} = 4 \)
Thus
\( \cos\theta = \dfrac{B}{H} = \dfrac{4}{5} \)
Example
If \( \tan\theta = 2 \), find the values of \( \sin\theta \) and \( \cos\theta \).
▶️ Answer / Explanation
Assume triangle with \( \tan\theta = \dfrac{P}{B} = 2 = \dfrac{2}{1} \)
Hypotenuse \( H = \sqrt{2^2 + 1^2} = \sqrt{5} \)
\( \sin\theta = \dfrac{P}{H} = \dfrac{2}{\sqrt{5}} \)
\( \cos\theta = \dfrac{1}{\sqrt{5}} \)
Example
If \( 3\sin\theta + 4\cos\theta = 5 \), find \( \sin\theta \) and \( \cos\theta \).
▶️ Answer / Explanation
We use the identity:
\( a\sin\theta + b\cos\theta = \sqrt{a^2 + b^2}\sin(\theta + \alpha) \)
Here \( a = 3, b = 4 \).
\( \sqrt{3^2 + 4^2} = 5 \)
Equation becomes:
\( 5\sin(\theta + \alpha) = 5 \Rightarrow \sin(\theta + \alpha) = 1 \)
So
\( \theta + \alpha = 90^\circ \)
Now find \( \alpha \) such that
\( \sin\alpha = \dfrac{4}{5},\quad \cos\alpha = \dfrac{3}{5} \)
Thus
\( \theta = 90^\circ – \alpha = 90^\circ – \cos^{-1}\left(\dfrac{3}{5}\right) \)
Then
\( \sin\theta = \dfrac{3}{5},\quad \cos\theta = \dfrac{4}{5} \)
Trigonometric Standard Angles
Standard angles are angles for which trigonometric ratios have exact values. These angles form the foundation of most JEE trigonometry calculations. Memorizing these values helps in solving equations, simplifying expressions, and evaluating identities without a calculator.
Radian to Degree Conversion Formulas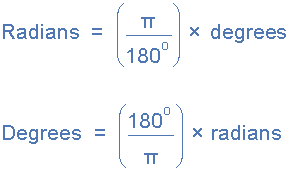
These are extremely important for JEE and must be memorized.
- \( 180^\circ = \pi\ \text{radians} \)
- \( 1\ \text{radian} = \dfrac{180^\circ}{\pi} \)
- \( 1^\circ = \dfrac{\pi}{180}\ \text{radians} \)
Standard Angles in Degrees and Radians
- \( 0^\circ = 0 \)
- \( 30^\circ = \dfrac{\pi}{6} \)
- \( 45^\circ = \dfrac{\pi}{4} \)
- \( 60^\circ = \dfrac{\pi}{3} \)
- \( 90^\circ = \dfrac{\pi}{2} \)
- \( 180^\circ = \pi \)
- \( 270^\circ = \dfrac{3\pi}{2} \)
- \( 360^\circ = 2\pi \)
General Conversion Formulas:
- To convert degrees to radians: \( \theta_{\text{radians}} = \theta_{\text{degrees}} \cdot \dfrac{\pi}{180} \)
- To convert radians to degrees: \( \theta_{\text{degrees}} = \theta_{\text{radians}} \cdot \dfrac{180}{\pi} \)
Examples of Conversions:
- \( 120^\circ = 120 \cdot \dfrac{\pi}{180} = \dfrac{2\pi}{3} \)
- \( \dfrac{5\pi}{6}\ \text{radians} = \dfrac{5\pi}{6} \cdot \dfrac{180}{\pi} = 150^\circ \)
Exact Trigonometric Values for Standard Angles
The following table shows exact values of the basic trigonometric ratios.
| \( \theta \) | \( \sin\theta \) | \( \cos\theta \) | \( \tan\theta \) |
| \( 0^\circ \) | 0 | 1 | 0 |
| \( 30^\circ \) | \( \dfrac{1}{2} \) | \( \dfrac{\sqrt{3}}{2} \) | \( \dfrac{1}{\sqrt{3}} \) |
| \( 45^\circ \) | \( \dfrac{1}{\sqrt{2}} \) | \( \dfrac{1}{\sqrt{2}} \) | 1 |
| \( 60^\circ \) | \( \dfrac{\sqrt{3}}{2} \) | \( \dfrac{1}{2} \) | \( \sqrt{3} \) |
| \( 90^\circ \) | 1 | 0 | Not defined |
Reciprocal Values for Standard Angles
- \( \csc 30^\circ = 2 \)
- \( \sec 60^\circ = 2 \)
- \( \cot 45^\circ = 1 \)
- \( \csc 45^\circ = \sqrt{2} \)
Example
Find the value of \( \sin 60^\circ \cos 30^\circ \).
▶️ Answer / Explanation
\( \sin 60^\circ = \dfrac{\sqrt{3}}{2} \), \( \cos 30^\circ = \dfrac{\sqrt{3}}{2} \)
Product \( = \dfrac{\sqrt{3}}{2} \cdot \dfrac{\sqrt{3}}{2} = \dfrac{3}{4} \)
Example
Evaluate \( \dfrac{\tan 45^\circ + \sin 30^\circ}{\cos 60^\circ} \).
▶️ Answer / Explanation
\( \tan 45^\circ = 1,\ \sin 30^\circ = \dfrac{1}{2},\ \cos 60^\circ = \dfrac{1}{2} \)
Expression \( = \dfrac{1 + \dfrac{1}{2}}{\dfrac{1}{2}} = \dfrac{\dfrac{3}{2}}{\dfrac{1}{2}} = 3 \)
Example
Simplify \( \dfrac{\sin 30^\circ + \sin 60^\circ}{\cos 45^\circ} \).
▶️ Answer / Explanation
\( \sin 30^\circ = \dfrac{1}{2} \), \( \sin 60^\circ = \dfrac{\sqrt{3}}{2} \), \( \cos 45^\circ = \dfrac{1}{\sqrt{2}} \)
Numerator \( = \dfrac{1}{2} + \dfrac{\sqrt{3}}{2} = \dfrac{1 + \sqrt{3}}{2} \)
Divide by \( \dfrac{1}{\sqrt{2}} \Rightarrow \) multiply by \( \sqrt{2} \)
\( = \dfrac{1 + \sqrt{3}}{2} \cdot \sqrt{2} = \dfrac{\sqrt{2} + \sqrt{6}}{2} \)
