IIT JEE Main Maths -Unit 2- Modulus and argument- Study Notes-New Syllabus
IIT JEE Main Maths -Unit 2- Modulus and argument – Study Notes – New syllabus
IIT JEE Main Maths -Unit 2- Modulus and argument – Study Notes -IIT JEE Main Maths – per latest Syllabus.
Key Concepts:
- Modulus and Argument of a Complex Number
Modulus and Argument of a Complex Number
Let \( z = x + iy \) be a complex number, where \( x \) is the real part and \( y \) is the imaginary part.
1. Modulus of a Complex Number
The modulus of \( z \) is its distance from the origin on the Argand plane, denoted by \( |z| \).
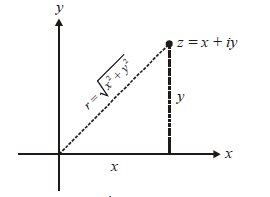
\( |z| = \sqrt{x^2 + y^2} \)
Geometrical Meaning: It represents the length of the line segment joining the origin \( (0, 0) \) and the point \( (x, y) \) on the complex plane.
2. Argument of a Complex Number
The argument (or amplitude) of \( z \) is the angle \( \theta \) made by the line joining the origin and the point \( (x, y) \) with the positive x-axis, measured in radians.
\( \tan \theta = \dfrac{y}{x} \)
The argument is denoted by \( \arg(z) \). Its principal value lies between \( -\pi \) and \( \pi \).
Polar Form: Every complex number can be expressed as
\( z = r(\cos \theta + i \sin \theta) \)
where \( r = |z| \) and \( \theta = \arg(z) \).
3. Argument in Different Quadrants
| Quadrant | x | y | Argument (θ) |
|---|---|---|---|
I | + | + | \( \tan^{-1}\left(\dfrac{y}{x}\right) \) |
II | − | + | \( \pi – \tan^{-1}\left(\dfrac{y}{|x|}\right) \) |
III | − | − | \( -\pi + \tan^{-1}\left(\dfrac{y}{x}\right) \) |
IV | + | − | \( -\tan^{-1}\left(\dfrac{|y|}{x}\right) \) |
Example
Find the modulus and argument of \( z = 3 + 4i \).
▶️ Answer / Explanation
Step 1: \( |z| = \sqrt{3^2 + 4^2} = 5 \)
Step 2: \( \tan \theta = \dfrac{4}{3} \Rightarrow \theta = \tan^{-1}\left(\dfrac{4}{3}\right) = 53.13^\circ = \dfrac{\pi}{3.39} \)
Answer: \( |z| = 5, \; \arg(z) = 53.13^\circ \)
Example
Find the modulus and argument of \( z = -2 + 2\sqrt{3}i \).
▶️ Answer / Explanation
Step 1: \( |z| = \sqrt{(-2)^2 + (2\sqrt{3})^2} = \sqrt{4 + 12} = 4 \)
Step 2: \( \tan \theta = \dfrac{2\sqrt{3}}{-2} = -\sqrt{3} \)
The point \((-2, 2\sqrt{3})\) lies in the second quadrant.
So, \( \theta = \pi – \dfrac{\pi}{3} = \dfrac{2\pi}{3} \)
Answer: \( |z| = 4, \; \arg(z) = \dfrac{2\pi}{3} \)
Example 3
Find the modulus and argument of \( z = -3 – 3i \).
▶️ Answer / Explanation
Step 1: \( |z| = \sqrt{(-3)^2 + (-3)^2} = \sqrt{18} = 3\sqrt{2} \)
Step 2: \( \tan \theta = \dfrac{-3}{-3} = 1 \)
Point \((-3, -3)\) lies in the third quadrant.
\( \theta = \pi + \dfrac{\pi}{4} = \dfrac{5\pi}{4} \) or equivalently \( -\dfrac{3\pi}{4} \) (principal value).
Answer: \( |z| = 3\sqrt{2}, \; \arg(z) = -\dfrac{3\pi}{4} \)