IIT JEE Main Maths -Unit 3- Adjoint and inverse of a square matrix- Study Notes-New Syllabus
IIT JEE Main Maths -Unit 3- Adjoint and inverse of a square matrix – Study Notes – New syllabus
IIT JEE Main Maths -Unit 3- Adjoint and inverse of a square matrix – Study Notes -IIT JEE Main Maths – per latest Syllabus.
Key Concepts:
- Adjoint of a Matrix
- Inverse of a Matrix
Adjoint of a Matrix
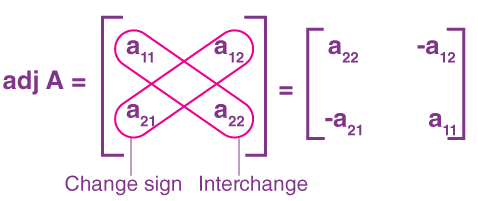
Let \( A = [a_{ij}]_{n \times n} \) be a square matrix. Then, the adjoint (or adjugate) of \( A \) is the transpose of the cofactor matrix of \( A \).
\( \text{adj}(A) = [A_{ij}]^T \)
where \( A_{ij} \) are the cofactors of the corresponding elements \( a_{ij} \).
Steps to Find adj(A):
- Find the cofactor of each element of \( A \).
- Form the cofactor matrix.
- Transpose the cofactor matrix → gives adj(A).
Properties of Adjoint Matrix
| Property | Statement |
|---|---|
| 1 | \( A \times \text{adj}(A) = \text{adj}(A) \times A = |A| I \) |
| 2 | \( \text{adj}(AB) = \text{adj}(B)\text{adj}(A) \) |
| 3 | \( \text{adj}(A^T) = (\text{adj}(A))^T \) |
| 4 | If \( A \) is singular (i.e., \( |A| = 0 \)), then \( \text{adj}(A) \) exists but \( A^{-1} \) does not. |
Inverse of a Matrix
If \( A \) is a non-singular square matrix (i.e., \( |A| \ne 0 \)), its inverse is defined as:
\( A^{-1} = \dfrac{1}{|A|} \text{adj}(A) \)
Note: A matrix is invertible only if \( |A| \ne 0 \). If \( |A| = 0 \), then \( A \) is called a singular matrix and has no inverse.
Verification Property
For a non-singular matrix \( A \):
\( A \times A^{-1} = A^{-1} \times A = I \)
Example
Find the adjoint and inverse of \( A = \begin{bmatrix}1 & 2\\3 & 4\end{bmatrix} \).
▶️ Answer / Explanation
Step 1: Find the cofactor matrix.
\( A_{11} = 4, \, A_{12} = -3, \, A_{21} = -2, \, A_{22} = 1 \)
So, cofactor matrix = \( \begin{bmatrix}4 & -3\\-2 & 1\end{bmatrix} \)
Step 2: Transpose → \( \text{adj}(A) = \begin{bmatrix}4 & -2\\-3 & 1\end{bmatrix} \)
Step 3: \( |A| = (1)(4) – (2)(3) = 4 – 6 = -2 \)
Step 4: \( A^{-1} = \dfrac{1}{|A|}\text{adj}(A) = \dfrac{-1}{2}\begin{bmatrix}4 & -2\\-3 & 1\end{bmatrix} = \begin{bmatrix}-2 & 1\\1.5 & -0.5\end{bmatrix} \)
Answer: \( \text{adj}(A) = \begin{bmatrix}4 & -2\\-3 & 1\end{bmatrix}, \quad A^{-1} = \begin{bmatrix}-2 & 1\\1.5 & -0.5\end{bmatrix} \)
Example
Find \( \text{adj}(A) \) for \( A = \begin{bmatrix}2 & 1 & 3\\1 & 0 & 2\\4 & 1 & 8\end{bmatrix} \).
▶️ Answer / Explanation
Step 1: Compute minors and cofactors:
- \( A_{11} = \begin{vmatrix}0 & 2\\1 & 8\end{vmatrix} = 0×8 – 2×1 = -2 \)
- \( A_{12} = (-1)^{1+2}\begin{vmatrix}1 & 2\\4 & 8\end{vmatrix} = – (8 – 8) = 0 \)
- \( A_{13} = (+1)\begin{vmatrix}1 & 0\\4 & 1\end{vmatrix} = 1×1 – 0×4 = 1 \)
Similarly, compute all cofactors:
$ \text{Cofactor matrix} = \begin{bmatrix} -2 & 0 & 1\\ -1 & 4 & -1\\ 2 & -1 & -2 \end{bmatrix} $
Step 2: \( \text{adj}(A) = (\text{Cofactor matrix})^T = \begin{bmatrix}-2 & -1 & 2\\0 & 4 & -1\\1 & -1 & -2\end{bmatrix} \)
Answer: \( \text{adj}(A) = \begin{bmatrix}-2 & -1 & 2\\0 & 4 & -1\\1 & -1 & -2\end{bmatrix} \)
Example
Find the inverse of \( A = \begin{bmatrix}1 & 2 & 3\\0 & 1 & 4\\5 & 6 & 0\end{bmatrix} \).
▶️ Answer / Explanation
Step 1: Compute \( |A| \) by expanding along the first row:
\( |A| = 1(1×0 – 4×6) – 2(0×0 – 4×5) + 3(0×6 – 1×5) \)
\( = 1(-24) – 2(-20) + 3(-5) = -24 + 40 – 15 = 1 \)
Step 2: Find cofactors (tedious but straightforward):
$ \text{Cofactor matrix} = \begin{bmatrix} -24 & 20 & -5\\ 18 & -15 & 4\\ 5 & -4 & 1 \end{bmatrix} $
Step 3: \( \text{adj}(A) = (\text{Cofactor matrix})^T = \begin{bmatrix}-24 & 18 & 5\\20 & -15 & -4\\-5 & 4 & 1\end{bmatrix} \)
Step 4: Since \( |A| = 1 \), \( A^{-1} = \text{adj}(A) \).
Answer: $ A^{-1} = \begin{bmatrix} -24 & 18 & 5\\ 20 & -15 & -4\\ -5 & 4 & 1 \end{bmatrix} $
Inverse of a Matrix
Definition
If \( A \) is a square matrix such that there exists another matrix \( B \) satisfying
\( AB = BA = I \)
then \( B \) is called the inverse of \( A \), and it is denoted by \( A^{-1} \).
Hence, \( A^{-1} \) exists only if \( A \) is a non-singular matrix (i.e., \( |A| \ne 0 \)).
Formula for Inverse
For a non-singular square matrix \( A \):

where \( \text{adj}(A) \) is the adjoint (transpose of cofactor matrix).
Condition for Existence
The inverse of \( A \) exists if and only if \( |A| \ne 0 \).
- If \( |A| = 0 \), then \( A \) is singular and has no inverse.
- If \( |A| \ne 0 \), then \( A \) is non-singular and \( A^{-1} \) exists.
Properties of Inverse Matrix
| Property | Statement |
|---|---|
| 1 | \( (A^{-1})^{-1} = A \) |
| 2 | \( (AB)^{-1} = B^{-1}A^{-1} \) |
| 3 | \( (A^T)^{-1} = (A^{-1})^T \) |
| 4 | If \( A \) is orthogonal, then \( A^{-1} = A^T \) |
Shortcut Formula for 2 × 2 Matrix
If \( A = \begin{bmatrix}a & b\\c & d\end{bmatrix} \), then
\( A^{-1} = \dfrac{1}{ad – bc} \begin{bmatrix}d & -b\\-c & a\end{bmatrix} \)
Verification Property
A matrix \( A \) and its inverse always satisfy:
\( A \times A^{-1} = A^{-1} \times A = I \)
Example
Find the inverse of \( A = \begin{bmatrix}4 & 3\\3 & 2\end{bmatrix} \).
▶️ Answer / Explanation
\( |A| = 4(2) – 3(3) = 8 – 9 = -1 \)
adj(A) = \( \begin{bmatrix}2 & -3\\-3 & 4\end{bmatrix} \)
\( A^{-1} = \dfrac{1}{-1} \begin{bmatrix}2 & -3\\-3 & 4\end{bmatrix} = \begin{bmatrix}-2 & 3\\3 & -4\end{bmatrix} \)
Answer: \( A^{-1} = \begin{bmatrix}-2 & 3\\3 & -4\end{bmatrix} \)
Example
Find the inverse of \( A = \begin{bmatrix}1 & 2 & 3\\0 & 1 & 4\\5 & 6 & 0\end{bmatrix} \).
▶️ Answer / Explanation
\( |A| = 1(1×0 – 4×6) – 2(0×0 – 4×5) + 3(0×6 – 1×5) \)
\( = 1(-24) – 2(-20) + 3(-5) = -24 + 40 – 15 = 1 \)
Cofactor matrix = $ \begin{bmatrix} -24 & 20 & -5\\ 18 & -15 & 4\\ 5 & -4 & 1 \end{bmatrix} $
So, \( \text{adj}(A) = \begin{bmatrix}-24 & 18 & 5\\20 & -15 & -4\\-5 & 4 & 1\end{bmatrix} \)
Since \( |A| = 1 \), \( A^{-1} = \text{adj}(A) \).
Answer: \( A^{-1} = \begin{bmatrix}-24 & 18 & 5\\20 & -15 & -4\\-5 & 4 & 1\end{bmatrix} \)
Example
Show that for \( A = \begin{bmatrix}2 & 3\\1 & 4\end{bmatrix} \), \( A \times A^{-1} = I \).
▶️ Answer / Explanation
\( |A| = 2(4) – 3(1) = 8 – 3 = 5 \)
\( \text{adj}(A) = \begin{bmatrix}4 & -3\\-1 & 2\end{bmatrix} \)
\( A^{-1} = \dfrac{1}{5}\begin{bmatrix}4 & -3\\-1 & 2\end{bmatrix} \)
Now, \( A \times A^{-1} = \begin{bmatrix}2 & 3\\1 & 4\end{bmatrix} \times \dfrac{1}{5}\begin{bmatrix}4 & -3\\-1 & 2\end{bmatrix} = \dfrac{1}{5}\begin{bmatrix}8 – 3 & -6 + 6\\4 – 4 & -3 + 8\end{bmatrix} = \dfrac{1}{5}\begin{bmatrix}5 & 0\\0 & 5\end{bmatrix} = I \)
Hence proved: \( A \times A^{-1} = I \).
