IIT JEE Main Maths -Unit 3- Consistency and solution of linear equations (2 or 3 variables)- Study Notes-New Syllabus
IIT JEE Main Maths -Unit 3- Consistency and solution of linear equations (2 or 3 variables) – Study Notes – New syllabus
IIT JEE Main Maths -Unit 3- Consistency and solution of linear equations (2 or 3 variables) – Study Notes -IIT JEE Main Maths – per latest Syllabus.
Key Concepts:
- Applications of Determinants and Matrices
- Properties and Applications of Inverse Matrix — Orthogonal and Singular Transformations
Applications of Determinants and Matrices — Consistency and Solving System of Linear Equations (Cramer’s Rule & Matrix Method)
Introduction
Determinants and matrices are powerful tools for solving systems of linear equations of the form:
$ a_1x + b_1y + c_1z = d_1\\ a_2x + b_2y + c_2z = d_2\\ a_3x + b_3y + c_3z = d_3 $
This system can be represented in matrix form as:
$ A X = B $
where
- \( A = \begin{bmatrix}a_1 & b_1 & c_1\\ a_2 & b_2 & c_2\\ a_3 & b_3 & c_3\end{bmatrix} \) — coefficient matrix
- \( X = \begin{bmatrix}x\\y\\z\end{bmatrix} \) — variable matrix
- \( B = \begin{bmatrix}d_1\\d_2\\d_3\end{bmatrix} \) — constant matrix
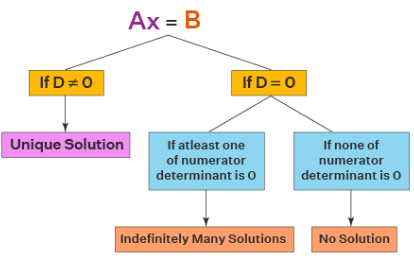
Consistency of a System
Let \( A X = B \) represent a system of equations.
- If \( |A| \ne 0 \), the system is consistent and has a unique solution.
- If \( |A| = 0 \), the system may be consistent (infinite solutions) or inconsistent (no solution) depending on \( \text{adj}(A)B = 0 \) or not.
Condition Summary:
| Case | Condition | Nature of Solutions |
|---|---|---|
| 1 | \( |A| \ne 0 \) | Unique solution (consistent) |
| 2 | \( |A| = 0 \) and \( \text{adj}(A)B = 0 \) | Infinitely many solutions (consistent) |
| 3 | \( |A| = 0 \) and \( \text{adj}(A)B \ne 0 \) | No solution (inconsistent) |
Cramer’s Rule (for 2 or 3 Variables)
If \( |A| \ne 0 \), the system has a unique solution given by:
$ x = \dfrac{|A_x|}{|A|}, \quad y = \dfrac{|A_y|}{|A|}, \quad z = \dfrac{|A_z|}{|A|} $
where \( A_x, A_y, A_z \) are obtained by replacing the 1st, 2nd, and 3rd columns of \( A \) with \( B \), respectively.
Matrix Method
For \( A X = B \):
If \( |A| \ne 0 \), then multiplying both sides by \( A^{-1} \):
\( A^{-1} A X = A^{-1} B \Rightarrow X = A^{-1} B \)
This gives a compact and powerful method to find \( x, y, z \).
Example
Solve the equations using Cramer’s rule:
$ 2x + 3y = 8\\ x + 2y = 5 $
▶️ Answer / Explanation
\( |A| = \begin{vmatrix}2 & 3\\1 & 2\end{vmatrix} = 4 – 3 = 1 \)
\( |A_x| = \begin{vmatrix}8 & 3\\5 & 2\end{vmatrix} = 16 – 15 = 1 \)
\( |A_y| = \begin{vmatrix}2 & 8\\1 & 5\end{vmatrix} = 10 – 8 = 2 \)
\( x = \dfrac{1}{1} = 1, \quad y = \dfrac{2}{1} = 2 \)
Answer: \( x = 1, y = 2 \)
Example
Solve the system using matrix method:
$ x + 2y + 3z = 10\\ 2x + 3y + z = 8\\ 3x + y + 2z = 9 $
▶️ Answer / Explanation
\( A = \begin{bmatrix}1 & 2 & 3\\2 & 3 & 1\\3 & 1 & 2\end{bmatrix}, \quad B = \begin{bmatrix}10\\8\\9\end{bmatrix} \)
\( |A| = 1(3×2 – 1×1) – 2(2×2 – 1×3) + 3(2×1 – 3×3) = 1(5) – 2(1) + 3(-7) = 5 – 2 – 21 = -18 \)
Find \( A^{-1} \) using adjoint (skipped steps for brevity): \( A^{-1} = \dfrac{1}{-18}\begin{bmatrix}5 & -1 & -7\\-4 & -7 & 11\\2 & 13 & -11\end{bmatrix} \)
\( X = A^{-1}B = \dfrac{1}{-18} \begin{bmatrix}5 & -1 & -7\\-4 & -7 & 11\\2 & 13 & -11\end{bmatrix} \begin{bmatrix}10\\8\\9\end{bmatrix} = \begin{bmatrix}1\\2\\3\end{bmatrix} \)
Answer: \( x = 1, y = 2, z = 3 \)
Example
Examine the consistency of the system:
$ x + y + z = 6\\ 2x + 3y + z = 10\\ 3x + 4y + 2z = 14 $
▶️ Answer / Explanation
\( A = \begin{bmatrix}1 & 1 & 1\\2 & 3 & 1\\3 & 4 & 2\end{bmatrix}, \quad B = \begin{bmatrix}6\\10\\14\end{bmatrix} \)
\( |A| = 1(3×2 – 1×4) – 1(2×2 – 1×3) + 1(2×4 – 3×3) = (2) – (1) + (-1) = 0 \)
Since \( |A| = 0 \), check \( \text{adj}(A)B \): After computation, \( \text{adj}(A)B = 0 \).
Hence, the system is consistent and has infinitely many solutions.
Key Takeaways for JEE:
- Use Cramer’s Rule for small systems (2×2 or 3×3).
- Matrix method \( X = A^{-1}B \) is compact and direct for unique solutions.
- Always check \( |A| \) first for consistency.
- If \( |A| = 0 \) and \( \text{adj}(A)B \ne 0 \), → No solution (inconsistent).
- If \( |A| = 0 \) and \( \text{adj}(A)B = 0 \), → Infinite solutions (consistent).
Properties and Applications of Inverse Matrix — Orthogonal and Singular Transformations
Recap — Inverse of a Matrix
If \( A \) is a square matrix and \( |A| \ne 0 \), its inverse exists and is given by:
\( A^{-1} = \dfrac{1}{|A|} \text{adj}(A) \)
The inverse satisfies the relation:
\( A A^{-1} = A^{-1} A = I \)
Singular and Non-Singular Matrices
| Type | Condition | Inverse Exists? |
|---|---|---|
| Non-Singular Matrix | \( |A| \ne 0 \) | Yes |
| Singular Matrix | \( |A| = 0 \) | No |
Orthogonal Matrix
A square matrix \( A \) is called orthogonal if:
\( A^T A = A A^T = I \)
Hence, \( A^{-1} = A^T \)
Properties of Orthogonal Matrices:
- All orthogonal matrices are non-singular.
- \( |A| = \pm 1 \).
- The product of two orthogonal matrices is orthogonal.
- The transpose of an orthogonal matrix is also orthogonal.
Applications of Inverse in Linear Transformations
Matrices can represent linear transformations like rotation, reflection, and scaling. If \( T \) is a transformation represented by matrix \( A \), then the inverse transformation \( T^{-1} \) is represented by \( A^{-1} \).
Example:
If a rotation in 2D space is represented by $ R = \begin{bmatrix} \cos\theta & -\sin\theta\\ \sin\theta & \cos\theta \end{bmatrix}, $ then
$ R^{-1} = R^T = \begin{bmatrix} \cos\theta & \sin\theta\\ -\sin\theta & \cos\theta \end{bmatrix} $ represents the inverse (rotation by \(-\theta\)).
Properties of Inverse Matrices (Extended)
| Property | Statement |
|---|---|
| 1 | \( (A^{-1})^{-1} = A \) |
| 2 | \( (AB)^{-1} = B^{-1}A^{-1} \) |
| 3 | \( (A^T)^{-1} = (A^{-1})^T \) |
| 4 | If \( A \) is orthogonal, \( A^{-1} = A^T \) |
| 5 | If \( A \) is invertible, then \( (kA)^{-1} = \dfrac{1}{k}A^{-1} \) |
Example
Show that \( A = \begin{bmatrix}\cos\theta & -\sin\theta\\\sin\theta & \cos\theta\end{bmatrix} \) is orthogonal.
▶️ Answer / Explanation
Compute \( A^T A \):
$ A^T = \begin{bmatrix}\cos\theta & \sin\theta\\-\sin\theta & \cos\theta\end{bmatrix} $
$ A^T A = \begin{bmatrix}\cos\theta & \sin\theta\\-\sin\theta & \cos\theta\end{bmatrix} \begin{bmatrix}\cos\theta & -\sin\theta\\\sin\theta & \cos\theta\end{bmatrix} = \begin{bmatrix}\cos^2\theta + \sin^2\theta & 0\\0 & \cos^2\theta + \sin^2\theta\end{bmatrix} = I $
Hence proved: \( A \) is orthogonal and \( A^{-1} = A^T \).
Example
Find \( A^{-1} \) if \( A = \begin{bmatrix}2 & 1\\7 & 4\end{bmatrix} \) and verify \( A A^{-1} = I \).
▶️ Answer / Explanation
\( |A| = 2(4) – 7(1) = 8 – 7 = 1 \)
\( \text{adj}(A) = \begin{bmatrix}4 & -1\\-7 & 2\end{bmatrix} \)
\( A^{-1} = \dfrac{1}{1} \begin{bmatrix}4 & -1\\-7 & 2\end{bmatrix} = \begin{bmatrix}4 & -1\\-7 & 2\end{bmatrix} \)
Check: $ A A^{-1} = \begin{bmatrix}2 & 1\\7 & 4\end{bmatrix}\begin{bmatrix}4 & -1\\-7 & 2\end{bmatrix} = \begin{bmatrix}8 – 7 & -2 + 2\\28 – 28 & -7 + 8\end{bmatrix} = I $
Hence verified.
Example
Given that a transformation matrix \( T = \begin{bmatrix}0 & -1\\1 & 0\end{bmatrix} \) rotates a vector 90° anticlockwise, find \( T^{-1} \) and explain its effect.
▶️ Answer / Explanation
\( T^T = \begin{bmatrix}0 & 1\\-1 & 0\end{bmatrix} \)
\( T^T T = I \Rightarrow T^{-1} = T^T \)
\( T^{-1} = \begin{bmatrix}0 & 1\\-1 & 0\end{bmatrix} \) represents a rotation by −90° (clockwise).
Conclusion: The inverse of a rotation matrix rotates by the same angle in the opposite direction.
