IIT JEE Main Maths -Unit 3- Determinants (order 2 and 3)- Study Notes-New Syllabus
IIT JEE Main Maths -Unit 3- Determinants (order 2 and 3) – Study Notes – New syllabus
IIT JEE Main Maths -Unit 3- Determinants (order 2 and 3) – Study Notes -IIT JEE Main Maths – per latest Syllabus.
Key Concepts:
- Definition of a Determinant
Definition of a Determinant
Every square matrix is associated with a unique scalar value called its determinant. If \( A \) is a square matrix of order \( n \), then its determinant is denoted by \( \det(A) \) or \( |A| \).
Determinants are defined only for square matrices.
Determinant of a 2 × 2 Matrix
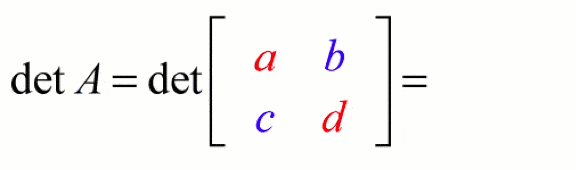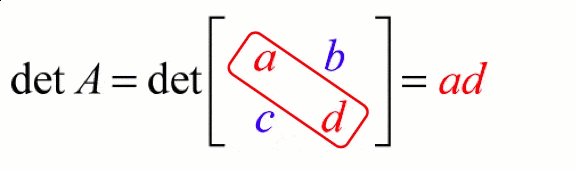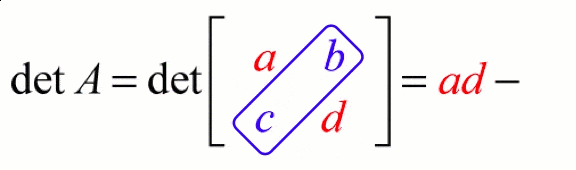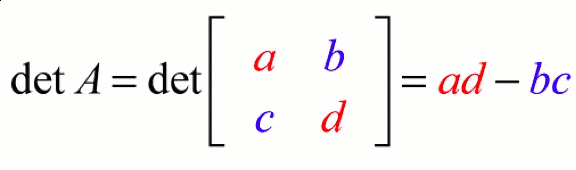
If \( A = \begin{bmatrix} a & b \\ c & d \end{bmatrix} \), then
\( |A| = ad – bc \)
Note: The determinant represents the signed area of the parallelogram formed by its row (or column) vectors.
Determinant of a 3 × 3 Matrix
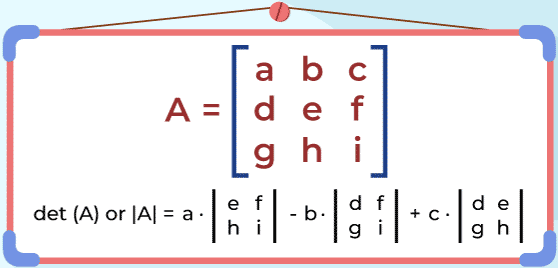
If \( A = \begin{bmatrix} a_1 & b_1 & c_1 \\ a_2 & b_2 & c_2 \\ a_3 & b_3 & c_3 \end{bmatrix} \), then
$ |A| = a_1(b_2c_3 – b_3c_2) – b_1(a_2c_3 – a_3c_2) + c_1(a_2b_3 – a_3b_2) $
This is called expansion along the first row. You can also expand along any row or column using minors and cofactors.
Determinant Notation
For \( A = \begin{bmatrix} a_{11} & a_{12} & a_{13}\\ a_{21} & a_{22} & a_{23}\\ a_{31} & a_{32} & a_{33} \end{bmatrix} \):
$ |A| = a_{11}(a_{22}a_{33} – a_{23}a_{32}) – a_{12}(a_{21}a_{33} – a_{23}a_{31}) + a_{13}(a_{21}a_{32} – a_{22}a_{31}) $
Properties of Determinants (Basic)
| Property | Statement |
|---|---|
| 1 | If any two rows (or columns) are interchanged, the sign of the determinant changes. |
| 2 | If any two rows (or columns) are identical, then \( |A| = 0 \). |
| 3 | If all elements of a row (or column) are multiplied by \( k \), the determinant is multiplied by \( k \). |
| 4 | If any row (or column) is multiplied by a number and added to another row (or column), the determinant remains unchanged. |
| 5 | \( |A^T| = |A| \) (determinant of a transpose is same as the determinant of the matrix). |
Example
Find the determinant of \( A = \begin{bmatrix} 2 & 3 \\ 4 & 5 \end{bmatrix} \).
▶️ Answer / Explanation
\( |A| = (2)(5) – (3)(4) = 10 – 12 = -2 \)
Hence, \( |A| = -2 \).
Example
Find the determinant of \( A = \begin{bmatrix} 1 & 2 & 3 \\ 4 & 5 & 6 \\ 7 & 8 & 9 \end{bmatrix} \).
▶️ Answer / Explanation
Expanding along the first row:
\( |A| = 1(5×9 – 6×8) – 2(4×9 – 6×7) + 3(4×8 – 5×7) \)
\( = 1(45 – 48) – 2(36 – 42) + 3(32 – 35) \)
\( = (-3) – 2(-6) + 3(-3) = -3 + 12 – 9 = 0 \)
Hence, \( |A| = 0 \).
(Note: Rows are in arithmetic progression → determinant = 0)
Example
Evaluate the determinant: $ \begin{vmatrix} \sin^2\theta & 1 & \cos^2\theta\\ 1 & \cos^2\theta & \sin^2\theta\\ \cos^2\theta & \sin^2\theta & 1 \end{vmatrix}$
▶️ Answer / Explanation
Let \( \sin^2\theta = S \) and \( \cos^2\theta = C \).
\( |A| = \begin{vmatrix} S & 1 & C\\ 1 & C & S\\ C & S & 1 \end{vmatrix} \)
Expanding along first row:
\( |A| = S(C – S) – 1(1 – CS) + C(1 – C) \)
Simplify: \( |A| = S(C – S) – (1 – CS) + C(1 – C) \)
\( = SC – S^2 – 1 + CS + C – C^2 \)
\( = 2SC – (S^2 + C^2) + (C – 1) \)
Using \( S + C = 1 \Rightarrow S^2 + C^2 = 1 – 2SC \),
\( |A| = 2SC – (1 – 2SC) + (C – 1) = 4SC – 2 + C \)
Substitute back \( S = \sin^2\theta, C = \cos^2\theta \): \( |A| = 4\sin^2\theta\cos^2\theta – 2 + \cos^2\theta \)
Hence, determinant simplifies to an expression in θ.
