IIT JEE Main Maths -Unit 3- Properties of determinants- Study Notes-New Syllabus
IIT JEE Main Maths -Unit 3- Properties of determinants – Study Notes – New syllabus
IIT JEE Main Maths -Unit 3- Properties of determinants – Study Notes -IIT JEE Main Maths – per latest Syllabus.
Key Concepts:
- Properties of Determinants (Advanced)
- Minors and Cofactors
Properties of Determinants (Advanced)
Determinants possess several algebraic properties that allow simplification without directly expanding them. These properties are especially useful in JEE questions where direct expansion is time-consuming.
Important Properties of Determinants
| No. | Property | Result |
|---|---|---|
| 1 | Interchanging two rows (or columns) | The sign of the determinant changes. |
| 2 | If two rows (or columns) are identical or proportional | Determinant = 0 |
| 3 | Multiplying one row (or column) by a scalar \( k \) | Determinant multiplied by \( k \) |
| 4 | If a constant multiple of one row (or column) is added to another | Determinant remains unchanged |
| 5 | If all elements of a row (or column) are zero | Determinant = 0 |
| 6 | If we multiply entire matrix by \( k \) | \( |kA| = k^n |A| \), where \( n \) = order of the matrix |
| 7 | Transpose Property | \( |A^T| = |A| \) |
| 8 | If any two rows (or columns) are interchanged twice | The determinant remains unchanged |
| 9 | If all rows (or columns) are added together to form a new row | The determinant remains unchanged |
Simplification Using Row and Column Operations
By applying elementary transformations such as:
- \( R_i \leftrightarrow R_j \) (interchange of rows)
- \( R_i \to kR_i \) (multiplying a row by \( k \))
- \( R_i \to R_i + kR_j \) (adding a multiple of one row to another)
We can simplify a determinant without changing its value (except for sign/scalar adjustments).
Example
Evaluate \( \begin{vmatrix} 2 & 3 \\ 4 & 6 \end{vmatrix} \).
▶️ Answer / Explanation
\( |A| = (2)(6) – (3)(4) = 12 – 12 = 0 \)
Since the second row is a multiple of the first, the determinant is zero.
Example
Evaluate: $ \begin{vmatrix} 1 & 2 & 3\\ 2 & 4 & 6\\ 1 & 1 & 1 \end{vmatrix}$ using determinant properties.
▶️ Answer / Explanation
Step 1: Observe that \( R_2 = 2R_1 \).
Step 2: Since two rows are proportional, \( |A| = 0 \).
Conclusion: Determinant = 0 (no expansion needed).
Example
Evaluate: $ \begin{vmatrix} 1 & a & a^2\\ 1 & b & b^2\\ 1 & c & c^2 \end{vmatrix} $
▶️ Answer / Explanation
Step 1: Subtract \( R_1 \) from \( R_2 \) and \( R_3 \):
\( R_2 \to R_2 – R_1, \quad R_3 \to R_3 – R_1 \)
\( |A| = \begin{vmatrix} 1 & a & a^2\\ 0 & b – a & b^2 – a^2\\ 0 & c – a & c^2 – a^2 \end{vmatrix} \)
Step 2: Expand along the first column:
\( |A| = 1 \times \begin{vmatrix} b – a & b^2 – a^2\\ c – a & c^2 – a^2 \end{vmatrix} \)
Step 3: Simplify: \( |A| = (b – a)(c^2 – a^2) – (c – a)(b^2 – a^2) \)
\( = (b – a)(c – a)(c + a) – (c – a)(b – a)(b + a) \)
\( = (b – a)(c – a)[(c + a) – (b + a)] = (b – a)(c – a)(c – b) \)
Conclusion: \[ \boxed{|A| = (b – a)(c – a)(c – b)} \]
This is a standard determinant form often used in JEE problems.
Minors and Cofactors
In determinants of order higher than 2, each element contributes to the overall value through a specific minor and cofactor. Understanding these concepts is essential for determinant expansion, inverse matrices, and adjoint calculations.
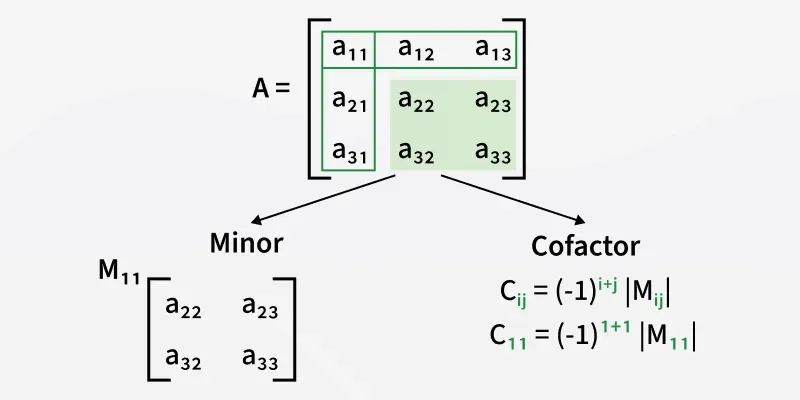
Minor of an Element
The minor of an element \( a_{ij} \) in a determinant is the determinant obtained by deleting the \( i^{th} \) row and \( j^{th} \) column of the original matrix.
It is denoted by \( M_{ij} \).
Example:
For $ A = \begin{bmatrix} 1 & 2 & 3\\ 4 & 5 & 6\\ 7 & 8 & 9 \end{bmatrix} $
the minor of \( a_{11} \) (which is 1) is
$ M_{11} = \begin{vmatrix} 5 & 6\\ 8 & 9 \end{vmatrix} = 45 – 48 = -3 $
Cofactor of an Element
The cofactor of an element \( a_{ij} \) is given by:
\( A_{ij} = (-1)^{i+j} \cdot M_{ij} \)
Here, \( (-1)^{i+j} \) gives the correct sign pattern (alternating + and -).
Sign Pattern of Cofactors
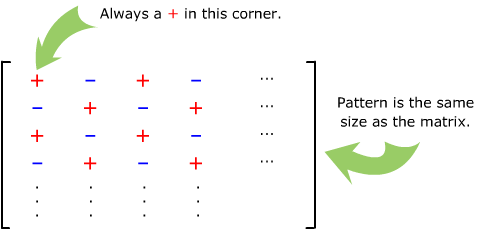
The signs of the cofactors for a 3 × 3 determinant are arranged as follows:
| + | − | + |
| − | + | − |
| + | − | + |
Expansion of a Determinant Using Minors and Cofactors
For a 3 × 3 determinant, expansion along the first row is:
$ |A| = a_{11}A_{11} + a_{12}A_{12} + a_{13}A_{13} $
You can expand along any row or column by multiplying each element with its cofactor.
Properties of Cofactors
| Property | Statement |
|---|---|
| 1 | Sum of the product of elements of any row (or column) with the cofactors of another row (or column) is zero. |
| 2 | Sum of the product of elements of any row (or column) with the cofactors of the same row (or column) gives the determinant value. |
$ a_{i1}A_{i1} + a_{i2}A_{i2} + a_{i3}A_{i3} = |A| $ and
$ a_{i1}A_{j1} + a_{i2}A_{j2} + a_{i3}A_{j3} = 0 \text{ (if } i \ne j) $
Example
Find the minor and cofactor of the element \( a_{11} = 1 \) in \( A = \begin{bmatrix}1 & 2 & 3\\4 & 5 & 6\\7 & 8 & 9\end{bmatrix} \).
▶️ Answer / Explanation
Minor \( M_{11} = \begin{vmatrix}5 & 6\\8 & 9\end{vmatrix} = 45 – 48 = -3 \)
Cofactor \( A_{11} = (+1) \times M_{11} = -3 \)
Answer: \( M_{11} = -3, \, A_{11} = -3 \)
Example
Find the determinant of \( A = \begin{bmatrix}2 & 3 & 1\\4 & 5 & 2\\6 & 7 & 3\end{bmatrix} \) by expanding along the second row.
▶️ Answer / Explanation
Expand along row 2:
\( |A| = 4A_{21} + 5A_{22} + 2A_{23} \)
Compute minors:
- \( M_{21} = \begin{vmatrix}3 & 1\\7 & 3\end{vmatrix} = 9 – 7 = 2 \)
- \( M_{22} = \begin{vmatrix}2 & 1\\6 & 3\end{vmatrix} = 6 – 6 = 0 \)
- \( M_{23} = \begin{vmatrix}2 & 3\\6 & 7\end{vmatrix} = 14 – 18 = -4 \)
Now cofactors:
\( A_{21} = (-1)^{2+1}M_{21} = -2, \; A_{22} = (+1)(0) = 0, \; A_{23} = (-1)^{2+3}(-4) = 4 \)
\( |A| = 4(-2) + 5(0) + 2(4) = -8 + 0 + 8 = 0 \)
Answer: \( |A| = 0 \)
Example
Verify that for \( A = \begin{bmatrix}1 & 2 & 3\\2 & 3 & 4\\3 & 4 & 5\end{bmatrix} \), the sum of products of elements of the first row and their cofactors equals the determinant of A.
▶️ Answer / Explanation
Step 1: Expand \( |A| \) along the first row:
\( |A| = 1A_{11} + 2A_{12} + 3A_{13} \)
Step 2: Compute minors:
- \( M_{11} = \begin{vmatrix}3 & 4\\4 & 5\end{vmatrix} = 15 – 16 = -1 \)
- \( M_{12} = \begin{vmatrix}2 & 4\\3 & 5\end{vmatrix} = 10 – 12 = -2 \)
- \( M_{13} = \begin{vmatrix}2 & 3\\3 & 4\end{vmatrix} = 8 – 9 = -1 \)
Step 3: Compute cofactors:
\( A_{11} = (-1)^{2}(-1) = -1 \), \( A_{12} = (-1)^{3}(-2) = 2 \), \( A_{13} = (-1)^{4}(-1) = -1 \)
Step 4: Substitute:
\( |A| = 1(-1) + 2(2) + 3(-1) = -1 + 4 – 3 = 0 \)
Conclusion: Verified that \( a_{11}A_{11} + a_{12}A_{12} + a_{13}A_{13} = |A| = 0 \).
