IIT JEE Main Maths -Unit 4- Fundamental principle of counting- Study Notes-New Syllabus
IIT JEE Main Maths -Unit 4- Fundamental principle of counting – Study Notes – New syllabus
IIT JEE Main Maths -Unit 4- Fundamental principle of counting – Study Notes -IIT JEE Main Maths – per latest Syllabus.
Key Concepts:
- Fundamental Principle of Counting
Fundamental Principle of Counting
The Fundamental Principle of Counting (FPC) is the basis for solving problems involving the number of possible outcomes of an event or a sequence of events.
It provides a systematic way to count total possibilities without listing them all individually.
Basic Rule (Multiplication Principle)
If one event can occur in \( m \) ways, and another independent event can occur in \( n \) ways, then the two events together can occur in \( m \times n \) ways.

$ \text{Total number of ways} = m \times n $
This can be extended to any number of events.
$ \text{If } E_1, E_2, \dots, E_k \text{ are independent events with } n_1, n_2, \dots, n_k \text{ ways, then} $
$ \text{Total number of outcomes} = n_1 \times n_2 \times \dots \times n_k $
Addition Principle
If one event can occur in \( m \) ways and another mutually exclusive event can occur in \( n \) ways, then exactly one of them can occur in \( m + n \) ways.
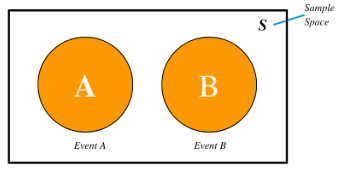
$ \text{Total number of ways} = m + n $
Condition: The events must be mutually exclusive (cannot happen together).
Difference Between Addition and Multiplication Principles
| Principle | Condition | Formula |
|---|---|---|
| Addition | Events are mutually exclusive | \( m + n \) |
| Multiplication | Events are independent (can occur together) | \( m \times n \) |
Example
A student has 3 shirts and 2 pairs of trousers. In how many different ways can he choose one shirt and one pair of trousers?
▶️ Answer / Explanation
Step 1: Number of ways to choose a shirt = 3
Step 2: Number of ways to choose trousers = 2
By multiplication principle:
\( \text{Total ways} = 3 \times 2 = 6 \)
Answer: 6 different outfits can be made.
Example
A password consists of 2 letters followed by 3 digits. If repetition of letters and digits is not allowed, find the total number of possible passwords.
▶️ Answer / Explanation
Step 1: There are 26 letters and 10 digits.
Letters part: \( 26 \) choices for the first × \( 25 \) for the second = \( 26 \times 25 \)
Digits part: \( 10 \) choices for the first × \( 9 \) × \( 8 \) for the next = \( 10 \times 9 \times 8 \)
Step 2: Total passwords = \( (26 \times 25) \times (10 \times 9 \times 8) \)
= \( 650 \times 720 = 468000 \)
Answer: 4,68,000 possible passwords.
Example
How many 4-digit even numbers can be formed using the digits 1, 2, 3, 4, 5, 6 without repetition?
▶️ Answer / Explanation
Step 1: Since the number must be even, the last digit must be 2, 4, or 6 (3 choices).
Step 2: After fixing the last digit, 5 digits remain for the first three places.
Number of ways to fill first three places = \( 5 \times 4 \times 3 = 60 \)
Step 3: Total 4-digit even numbers = \( 3 \times 60 = 180 \)
Answer: 180 four-digit even numbers can be formed.
