IIT JEE Main Maths -Unit 6- Insertion of means (A.M., G.M.,H.M.)- Study Notes-New Syllabus
IIT JEE Main Maths -Unit 6- Insertion of means (A.M., G.M.,H.M.) – Study Notes – New syllabus
IIT JEE Main Maths -Unit 6- Insertion of means (A.M., G.M.,H.M.) – Study Notes -IIT JEE Main Maths – per latest Syllabus.
Key Concepts:
- Arithmetic Mean (A.M.), Geometric Mean (G.M.), and Harmonic Mean (H.M.)
Arithmetic Mean (A.M.), Geometric Mean (G.M.), and Harmonic Mean (H.M.)
For any two positive numbers \( a \) and \( b \):
- Arithmetic Mean (A.M.): $ A = \dfrac{a + b}{2} $
- Geometric Mean (G.M.): $ G = \sqrt{ab} $
- Harmonic Mean (H.M.): $ H = \dfrac{2ab}{a + b} $
These are three important types of averages, often used in sequence and progression problems.
Relationship Between A.M., G.M., and H.M.
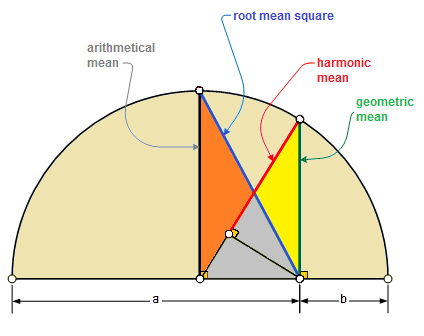
The three means satisfy the following relationship:
$ A \ge G \ge H $
Equality holds only when \( a = b \).
Also,
$ A \times H = G^2 $
Inserting Means
- Arithmetic Means: Between \( a \) and \( b \), insert \( n \) arithmetic means using A.P. logic.
- Geometric Means: Between \( a \) and \( b \), insert \( n \) geometric means using G.P. logic.
- Harmonic Means: Between \( a \) and \( b \), insert \( n \) harmonic means using reciprocals of A.P.
Note: If \( a, b, c \) are in A.P., then their reciprocals \( \dfrac{1}{a}, \dfrac{1}{b}, \dfrac{1}{c} \) are in H.P.
Relationship of Sequences
| Type | Pattern | Formula |
|---|---|---|
| A.P. | Equal difference | \( a_n = a + (n – 1)d \) |
| G.P. | Equal ratio | \( a_n = ar^{n – 1} \) |
| H.P. | Reciprocal of A.P. | \( \dfrac{1}{a_n} = \dfrac{1}{a} + (n – 1)d’ \) |
For More Than Two Numbers
For \( n \) positive numbers \( a_1, a_2, a_3, \dots, a_n \):
- Arithmetic Mean: $ A = \dfrac{a_1 + a_2 + \dots + a_n}{n} $
- Geometric Mean: $ G = (a_1 a_2 a_3 \dots a_n)^{1/n} $
- Harmonic Mean: $ H = \dfrac{n}{\dfrac{1}{a_1} + \dfrac{1}{a_2} + \dots + \dfrac{1}{a_n}} $
Example
Find A.M., G.M., and H.M. between 4 and 16.
▶️ Answer / Explanation
\( A = \dfrac{4 + 16}{2} = 10 \)
\( G = \sqrt{4 \times 16} = 8 \)
\( H = \dfrac{2 \times 4 \times 16}{4 + 16} = \dfrac{128}{20} = 6.4 \)
Answer: \( A = 10,\, G = 8,\, H = 6.4 \)
Example
Show that \( A \times H = G^2 \) for any two positive numbers \( a \) and \( b \).
▶️ Answer / Explanation
\( A = \dfrac{a + b}{2},\quad H = \dfrac{2ab}{a + b} \)
\( A \times H = \dfrac{a + b}{2} \times \dfrac{2ab}{a + b} = ab = G^2 \)
Hence proved: \( A \times H = G^2 \)
Example
Find A.M., G.M., and H.M. of the numbers 3, 6, and 12.
▶️ Answer / Explanation
\( A = \dfrac{3 + 6 + 12}{3} = \dfrac{21}{3} = 7 \)
\( G = (3 \times 6 \times 12)^{1/3} = (216)^{1/3} = 6 \)
\( H = \dfrac{3}{\dfrac{1}{3} + \dfrac{1}{6} + \dfrac{1}{12}} = \dfrac{3}{\dfrac{4 + 2 + 1}{12}} = \dfrac{3}{\dfrac{7}{12}} = \dfrac{36}{7} \approx 5.14 \)
Answer: \( A = 7,\, G = 6,\, H \approx 5.14 \)
Insertion of Means (A.M. and G.M.)
In mathematics, inserting means between two numbers allows us to form sequences — an Arithmetic Progression (A.P.) or a Geometric Progression (G.P.) — that begin and end with the given numbers.
Insertion of Arithmetic Means (A.M.s)
If we are to insert \( n \) Arithmetic Means between two numbers \( a \) and \( b \), then the sequence becomes an A.P.:
$ a,\, A_1,\, A_2,\, A_3,\, \dots,\, A_n,\, b $
Since the difference between consecutive terms is constant, the common difference \( d \) is given by:
$ d = \dfrac{b – a}{n + 1} $
The inserted means are:
$ A_k = a + kd, \quad (k = 1, 2, 3, \dots, n) $
Example: Inserting 3 A.M.s between 2 and 14
We are forming an A.P.: \( 2, A_1, A_2, A_3, 14 \)
\( d = \dfrac{14 – 2}{4} = 3 \)
Hence, inserted means are:
\( A_1 = 5, \, A_2 = 8, \, A_3 = 11 \)
Insertion of Geometric Means (G.M.s)
If we insert \( n \) Geometric Means between two positive numbers \( a \) and \( b \), then the sequence forms a G.P.:
$ a,\, G_1,\, G_2,\, G_3,\, \dots,\, G_n,\, b $
with common ratio:
$ r = \left( \dfrac{b}{a} \right)^{\dfrac{1}{n + 1}} $
The inserted means are given by:
$ G_k = ar^k, \quad (k = 1, 2, 3, \dots, n) $
Relationship Between A.M. and G.M.
For two positive numbers \( a \) and \( b \):
$ A.M. \ge G.M. \quad \text{and} \quad A \times H = G^2 $
Example
Insert 4 arithmetic means between 3 and 23.
▶️ Answer / Explanation
Given: \( a = 3, b = 23, n = 4 \)
Common difference: \( d = \dfrac{b – a}{n + 1} = \dfrac{23 – 3}{5} = 4 \)
Inserted means: \( 7, 11, 15, 19 \)
Answer: \( A_1 = 7, A_2 = 11, A_3 = 15, A_4 = 19 \)
Example
Insert 2 geometric means between 3 and 24.
▶️ Answer / Explanation
Given: \( a = 3, b = 24, n = 2 \)
\( r = \left( \dfrac{24}{3} \right)^{1/3} = (8)^{1/3} = 2 \)
Inserted means: \( 3r = 6, \, 3r^2 = 12 \)
Answer: \( G_1 = 6, G_2 = 12 \)
Example
The 2nd A.M. between two numbers is 12, and their G.M. is 9. Find the numbers.
▶️ Answer / Explanation
Let the numbers be \( a \) and \( b \).
2nd A.M. = 12 ⇒ \( A_2 = \dfrac{2a + 2b}{4} = \dfrac{a + b}{2} = 12 \Rightarrow a + b = 24 \).
G.M. = 9 ⇒ \( ab = 81 \).
Solving \( a + b = 24, ab = 81 \): \( a, b = 12 \pm \sqrt{12^2 – 81} = 12 \pm 9 \Rightarrow (a, b) = (3, 21) \text{ or } (21, 3) \).
Answer: Numbers are \( 3 \) and \( 21 \).
