IIT JEE Main Maths -Unit 6- Sum of n Terms of Special Series- Study Notes-New Syllabus
IIT JEE Main Maths -Unit 6- Sum of n Terms of Special Series – Study Notes – New syllabus
IIT JEE Main Maths -Unit 6- Sum of n Terms of Special Series – Study Notes -IIT JEE Main Maths – per latest Syllabus.
Key Concepts:
- Sum of n Terms of Special Series — Arithmetic–Geometric Progression (A.G.P.) and Infinite Series
- Sigma (Σ) Notation and Summation of Series (A.P., G.P., and A.G.P.)
Sum of n Terms of Special Series — Arithmetic–Geometric Progression (A.G.P.) and Infinite Series
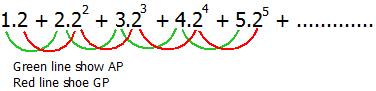
An Arithmetic–Geometric Progression (A.G.P.) is a sequence in which each term is the product of the corresponding terms of an A.P. and a G.P..
$\text{Example: } a,\, (a + d)r,\, (a + 2d)r^2,\, (a + 3d)r^3,\, \dots $
Here, \( a, a + d, a + 2d, \dots \) form an A.P., and \( 1, r, r^2, \dots \) form a G.P.
General Term of an A.G.P.
The \( n \)th term of an A.G.P. is:
$ T_n = (a + (n – 1)d)r^{n – 1}$
Sum of n Terms of an A.G.P.
Let \( S_n = a + (a + d)r + (a + 2d)r^2 + (a + 3d)r^3 + \dots + [a + (n – 1)d]r^{n – 1} \).
Multiply both sides by \( r \):
$rS_n = ar + (a + d)r^2 + (a + 2d)r^3 + \dots + [a + (n – 1)d]r^n $
Subtracting, we get:
\[ S_n – rS_n = a(1 – r^n) + dr(1 – (n)r^{n – 1} + (n – 1)r^n)/(1 – r)^2 \]
After simplification,
\[ S_n = \dfrac{a(1 – r^n)}{1 – r} + \dfrac{dr(1 – nr^{n – 1} + (n – 1)r^n)}{(1 – r)^2} \]
Note: This is valid only for \( r \ne 1 \).
Sum to Infinity of an A.G.P. (for |r| < 1)
When \( |r| < 1 \), \( r^n \to 0 \) as \( n \to \infty \). So the sum to infinity is:
\[ S_\infty = \dfrac{a}{1 – r} + \dfrac{dr}{(1 – r)^2} \]
Special Case: A.G.P. with d = 0 (reduces to a G.P.)
If the arithmetic part is constant (i.e. \( d = 0 \)), the A.G.P. becomes a simple G.P., and:
\[ S_n = \dfrac{a(1 – r^n)}{1 – r}, \quad S_\infty = \dfrac{a}{1 – r} \]
Example Patterns Common in JEE
- \( 1 + 2r + 3r^2 + 4r^3 + \dots \)
- \( 5 + 7r + 9r^2 + 11r^3 + \dots \)
- \( (a + d)r + (a + 2d)r^2 + (a + 3d)r^3 + \dots \)
All these are A.G.P.s and can be solved using the same formula.
Example
Find the sum to infinity of the series \( 1 + 2r + 3r^2 + 4r^3 + \dots \), where \( |r| < 1 \).
▶️ Answer / Explanation
Here \( a = 1, d = 1 \).
Formula: \( S_\infty = \dfrac{a}{1 – r} + \dfrac{dr}{(1 – r)^2} \)
\( S_\infty = \dfrac{1}{1 – r} + \dfrac{r}{(1 – r)^2} = \dfrac{1 – r + r}{(1 – r)^2} = \dfrac{1}{(1 – r)^2} \)
Answer: \( S_\infty = \dfrac{1}{(1 – r)^2} \)
Example
Find the sum of the first 5 terms of the series \( 5 + 7r + 9r^2 + 11r^3 + 13r^4 \), where \( r = \dfrac{1}{2} \).
▶️ Answer / Explanation
Here \( a = 5, d = 2, r = \dfrac{1}{2}, n = 5 \).
Formula: \( S_n = \dfrac{a(1 – r^n)}{1 – r} + \dfrac{dr(1 – nr^{n – 1} + (n – 1)r^n)}{(1 – r)^2} \)
Substitute values: \( S_5 = \dfrac{5(1 – (1/2)^5)}{1/2} + \dfrac{2(1/2)(1 – 5(1/2)^4 + 4(1/2)^5)}{(1/2)^2} \)
After simplification, \( S_5 = 9.3125 \).
Answer: \( S_5 = 9.3125 \)
Example
Find the sum to infinity of the series \( 2 + 5r + 8r^2 + 11r^3 + \dots \), where \( |r| < 1 \).
▶️ Answer / Explanation
Here \( a = 2, d = 3 \).
Formula: \( S_\infty = \dfrac{a}{1 – r} + \dfrac{dr}{(1 – r)^2} \)
\( S_\infty = \dfrac{2}{1 – r} + \dfrac{3r}{(1 – r)^2} \)
Combine: \( S_\infty = \dfrac{2(1 – r) + 3r}{(1 – r)^2} = \dfrac{2 + r}{(1 – r)^2} \)
Answer: \( S_\infty = \dfrac{2 + r}{(1 – r)^2} \)
Special Infinite Series Results (Very Useful in JEE)
- \( 1 + r + r^2 + r^3 + \dots = \dfrac{1}{1 – r}, \quad |r| < 1 \)
- \( 1 + 2r + 3r^2 + 4r^3 + \dots = \dfrac{1}{(1 – r)^2}, \quad |r| < 1 \)
- \( 1 + 4r + 9r^2 + 16r^3 + \dots = \dfrac{1 + r}{(1 – r)^3}, \quad |r| < 1 \)
Key Takeaways for JEE:
- A.G.P. combines A.P. and G.P. patterns — use the formula derived from multiplying by \( r \) and subtracting.
- For infinite A.G.P. → always check \( |r| < 1 \).
- Memorize \( S_\infty = \dfrac{a}{1 – r} + \dfrac{dr}{(1 – r)^2} \).
- Series like \( 1 + 2r + 3r^2 + \dots \) directly sum to \( \dfrac{1}{(1 – r)^2} \).
- Commonly appears in JEE under mixed series, limits, and sigma-notation problems.
Shortcut Recap Table
| Series Type | Sum (Finite) | Sum (Infinite) |
|---|---|---|
| G.P. | \( S_n = \dfrac{a(1 – r^n)}{1 – r} \) | \( S_\infty = \dfrac{a}{1 – r} \) |
| A.G.P. | \( S_n = \dfrac{a(1 – r^n)}{1 – r} + \dfrac{dr(1 – nr^{n – 1} + (n – 1)r^n)}{(1 – r)^2} \) | \( S_\infty = \dfrac{a}{1 – r} + \dfrac{dr}{(1 – r)^2} \) |
Sigma (Σ) Notation and Summation of Series (A.P., G.P., and A.G.P.)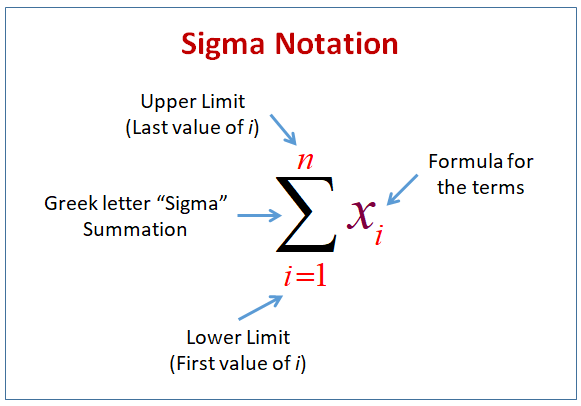
The symbol \( \Sigma \) (capital sigma) represents the sum of a sequence of terms.
$ \sum_{r=1}^{n} a_r = a_1 + a_2 + a_3 + \dots + a_n $
Here, \( a_r \) is the general term, and the index \( r \) varies from 1 to \( n \).
Basic Sigma Formulas (Very Important)
| Formula | Summation Value |
|---|---|
| \( \displaystyle \sum_{r=1}^{n} 1 \) | \( n \) |
| \( \displaystyle \sum_{r=1}^{n} r \) | \( \dfrac{n(n + 1)}{2} \) |
| \( \displaystyle \sum_{r=1}^{n} r^2 \) | \( \dfrac{n(n + 1)(2n + 1)}{6} \) |
| \( \displaystyle \sum_{r=1}^{n} r^3 \) | \( \left[\dfrac{n(n + 1)}{2}\right]^2 \) |
General Rule: $ \sum_{r=1}^{n} (a + br + cr^2 + \dots) = a\sum 1 + b\sum r + c\sum r^2 + \dots $
Summation of an Arithmetic Series (A.P.)
If the series is in A.P.: $ a,\, a + d,\, a + 2d,\, \dots,\, a + (n – 1)d $ then,
$ \sum_{r=1}^{n} (a + (r – 1)d) = \dfrac{n}{2}[2a + (n – 1)d] $
Summation of a Geometric Series (G.P.)
If the series is in G.P.: $ a,\, ar,\, ar^2,\, ar^3,\, \dots $ then,
$ \sum_{r=1}^{n} ar^{r – 1} = \dfrac{a(r^n – 1)}{r – 1}, \quad (r \ne 1) $
and if \( |r| < 1 \): $ S_\infty = \dfrac{a}{1 – r} $
Summation of an Arithmetic–Geometric Series (A.G.P.)
Series of the form: $ a + (a + d)r + (a + 2d)r^2 + \dots $ have the sum:
$ S_n = \dfrac{a(1 – r^n)}{1 – r} + \dfrac{dr(1 – nr^{n – 1} + (n – 1)r^n)}{(1 – r)^2} $
and if \( |r| < 1 \):
$ S_\infty = \dfrac{a}{1 – r} + \dfrac{dr}{(1 – r)^2} $
Properties of Sigma Notation
- \( \displaystyle \sum_{r=1}^{n} (a_r + b_r) = \sum a_r + \sum b_r \)
- \( \displaystyle \sum_{r=1}^{n} ka_r = k\sum a_r \)
- \( \displaystyle \sum_{r=1}^{n} (r + 1) = \sum r + \sum 1 = \dfrac{n(n + 1)}{2} + n \)
- \( \displaystyle \sum_{r=1}^{n} (n – r + 1) = \sum_{r=1}^{n} r = \dfrac{n(n + 1)}{2} \)
Shortcut Sigma Expansions (for Quick JEE Solving)
- \( \displaystyle \sum_{r=1}^{n} (a + br) = na + b\dfrac{n(n + 1)}{2} \)
- \( \displaystyle \sum_{r=1}^{n} (ar + br^2) = a\dfrac{n(n + 1)}{2} + b\dfrac{n(n + 1)(2n + 1)}{6} \)
- \( \displaystyle \sum_{r=1}^{n} r(r + 1) = \dfrac{n(n + 1)(n + 2)}{3} \)
- \( \displaystyle \sum_{r=1}^{n} r(r – 1) = \dfrac{n(n + 1)(n – 1)}{3} \)
Key Takeaways for JEE:
- Break complex sums into known forms using basic Σ formulas.
- Use Σ identities to simplify polynomial and mixed series.
- Always check for G.P. or A.G.P. patterns before expanding manually.
- For infinite geometric or A.G.P. series, ensure \( |r| < 1 \) for convergence.
- Remember the power sum formulas — they appear often in JEE algebra and calculus limits.
Common JEE Mistakes to Avoid
- Forgetting to apply limits correctly when starting from \( r = 0 \) or another index.
- Using A.P. formulas for geometric or mixed progressions.
- For infinite sums, forgetting to verify \( |r| < 1 \).
Example
Evaluate \( \displaystyle \sum_{r=1}^{10} (3r + 2) \).
▶️ Answer / Explanation
\( \sum (3r + 2) = 3\sum r + 2\sum 1 \)
\( = 3\left[\dfrac{10(11)}{2}\right] + 2(10) = 3(55) + 20 = 185 \)
Answer: 185
Example
Find \( \displaystyle \sum_{r=1}^{5} (r^2 + 2r) \).
▶️ Answer / Explanation
\( \sum (r^2 + 2r) = \sum r^2 + 2\sum r \)
\( = \dfrac{5(6)(11)}{6} + 2\left[\dfrac{5(6)}{2}\right] = 55 + 30 = 85 \)
Answer: 85
Example
Find the sum to infinity of the series \( 3 + 5r + 7r^2 + 9r^3 + \dots \), where \( |r| < 1 \).
▶️ Answer / Explanation
Here \( a = 3, d = 2 \).
Formula: \( S_\infty = \dfrac{a}{1 – r} + \dfrac{dr}{(1 – r)^2} \)
\( S_\infty = \dfrac{3}{1 – r} + \dfrac{2r}{(1 – r)^2} = \dfrac{3(1 – r) + 2r}{(1 – r)^2} = \dfrac{3 – r}{(1 – r)^2} \)
Answer: \( S_\infty = \dfrac{3 – r}{(1 – r)^2} \)
