IIT JEE Main Maths -Unit 7- Differentiability- Study Notes-New Syllabus
IIT JEE Main Maths -Unit 7- Differentiability – Study Notes – New syllabus
IIT JEE Main Maths -Unit 7- Differentiability – Study Notes -IIT JEE Main Maths – per latest Syllabus.
Key Concepts:
- Differentiability
Differentiability
The concept of differentiability measures how smoothly a function changes — it indicates whether a function has a well-defined tangent (slope) at a given point.
In simple terms, a function is differentiable at a point if it has a definite and finite derivative there.
Definition of Derivative at a Point
A function \( f(x) \) is said to be differentiable at \( x = a \) if the following limit exists and is finite:
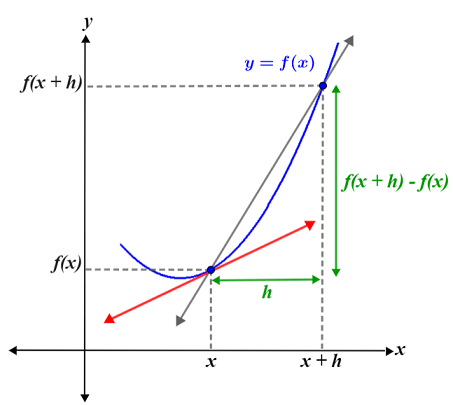
$ f'(a) = \lim_{h \to 0} \dfrac{f(a + h) – f(a)}{h} $
This value \( f'(a) \) represents the slope of the tangent to the curve \( y = f(x) \) at \( x = a \).
Left-Hand and Right-Hand Derivatives
At a given point \( x = a \), define:
$ \text{LHD} = \lim_{h \to 0^-} \dfrac{f(a + h) – f(a)}{h}, \quad \text{RHD} = \lim_{h \to 0^+} \dfrac{f(a + h) – f(a)}{h} $
Condition for differentiability at \( x = a \):
$ \text{LHD} = \text{RHD} $

If both derivatives exist and are equal → \( f(x) \) is differentiable at \( x = a \).
Relationship Between Continuity and Differentiability
- If a function is differentiable at a point, it must also be continuous there.
- But, if a function is continuous, it may or may not be differentiable.
Example: \( f(x) = |x| \) is continuous at \( x = 0 \), but not differentiable at \( x = 0 \).
Geometrical Meaning
The derivative \( f'(x) \) represents the slope of the tangent to the curve \( y = f(x) \) at that point.
If the function is not differentiable, the graph shows a sharp corner, cusp, or vertical tangent at that point.
Differentiability in an Interval
A function \( f(x) \) is said to be differentiable in an interval if it is differentiable at every point in that interval.
For a closed interval \([a, b]\):
- Right-hand derivative exists at \( a \).
- Left-hand derivative exists at \( b \).
- Function is differentiable for all interior points.
Conditions for Non-Differentiability
A function may fail to be differentiable at a point due to the following reasons:

- Corner point: LHD and RHD exist but are unequal (e.g., \( |x| \) at \( x = 0 \)).
- Cusp: LHD and RHD are infinite but of opposite sign (e.g., \( x^{2/3} \) at \( x = 0 \)).
- Vertical tangent: Both LHD and RHD → ±∞ (e.g., \( x^{1/3} \) at \( x = 0 \)).
- Discontinuity: Function not continuous at the point → not differentiable.
Algebra of Differentiable Functions
If \( f(x) \) and \( g(x) \) are differentiable at \( x = a \), then:
| Operation | Rule |
|---|---|
| Sum | \( (f + g)’ = f’ + g’ \) |
| Difference | \( (f – g)’ = f’ – g’ \) |
| Product | \( (fg)’ = f’g + fg’ \) |
| Quotient | \( \left(\dfrac{f}{g}\right)’ = \dfrac{f’g – fg’}{g^2}, \, g \ne 0 \) |
Example
Check differentiability of \( f(x) = x^2 \) at \( x = 2 \).
▶️ Answer / Explanation
Compute derivative using definition:
\( f'(2) = \lim_{h \to 0} \dfrac{(2 + h)^2 – 4}{h} = \lim_{h \to 0} \dfrac{4 + 4h + h^2 – 4}{h} = \lim_{h \to 0} (4 + h) = 4 \).
Both LHD and RHD are 4 ⇒ differentiable.
Answer: Differentiable at \( x = 2 \), derivative = 4.
Example
Check differentiability of \( f(x) = |x| \) at \( x = 0 \).
▶️ Answer / Explanation
For \( x > 0 \): \( f(x) = x \Rightarrow f'(x) = 1 \).
For \( x < 0 \): \( f(x) = -x \Rightarrow f'(x) = -1 \).
At \( x = 0 \): LHD = -1, RHD = +1 ⇒ not equal.
Answer: Not differentiable at \( x = 0 \) (corner point).
Example
Check differentiability of \( f(x) = x^{2/3} \) at \( x = 0 \).
▶️ Answer / Explanation
\( f'(x) = \dfrac{2}{3}x^{-1/3} \).
As \( x \to 0^- \), \( f'(x) \to -\infty \); as \( x \to 0^+ \), \( f'(x) \to +\infty \).
LHD and RHD have opposite signs ⇒ cusp at \( x = 0 \).
Answer: Not differentiable at \( x = 0 \).
