IIT JEE Main Maths -Unit 7- Mean Value Theorem and Rolle’s Theorem- Study Notes-New Syllabus
IIT JEE Main Maths -Unit 7- Mean Value Theorem and Rolle’s Theorem – Study Notes – New syllabus
IIT JEE Main Maths -Unit 7- Mean Value Theorem and Rolle’s Theorem – Study Notes -IIT JEE Main Maths – per latest Syllabus.
Key Concepts:
- Applications of Derivatives — Mean Value Theorem (MVT) and Rolle’s Theorem
Applications of Derivatives — Mean Value Theorem (MVT) and Rolle’s Theorem
The Mean Value Theorem and Rolle’s Theorem are two fundamental results in differential calculus that connect the average rate of change of a function with its instantaneous rate of change (derivative).
These theorems help us understand how the derivative behaves between two points and are essential tools in proving other calculus results.
Rolle’s Theorem — Statement
If a real-valued function \( f(x) \) satisfies the following three conditions on a closed interval \([a, b]\):
- \( f(x) \) is continuous on \([a, b]\).
- \( f(x) \) is differentiable on \((a, b)\).
- \( f(a) = f(b) \).
Then, there exists at least one point \( c \in (a, b) \) such that:
$ f'(c) = 0 $
Geometrical Meaning (Rolle’s Theorem)
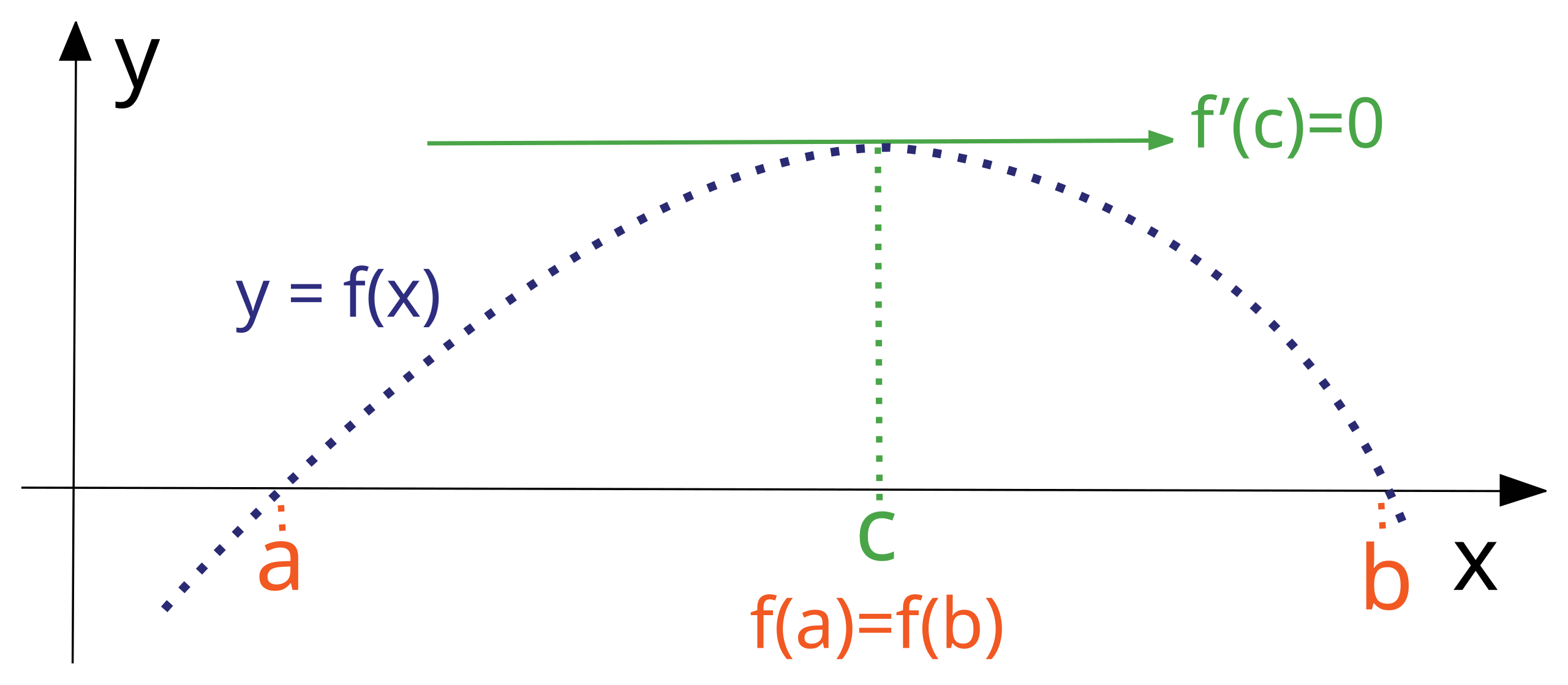
Rolle’s theorem guarantees that for a smooth curve joining two points with the same y-value, there is at least one point in between where the tangent is horizontal (slope = 0).
Mean Value Theorem (MVT) — Statement
If \( f(x) \) is:
- Continuous on \([a, b]\), and
- Differentiable on \((a, b)\),
Then there exists at least one \( c \in (a, b) \) such that:
$ f'(c) = \dfrac{f(b) – f(a)}{b – a} $
Geometrical Meaning (MVT)
The MVT states that there exists a point \( c \) between \( a \) and \( b \) where the slope of the tangent equals the slope of the secant joining the points \( (a, f(a)) \) and \( (b, f(b)) \).
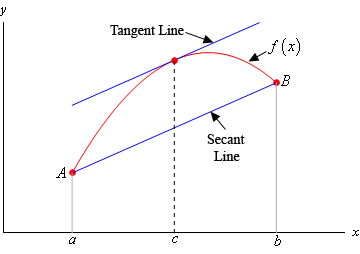
In other words, at some point, the instantaneous rate of change = average rate of change.
Relation Between Rolle’s Theorem and MVT
| Aspect | Rolle’s Theorem | Mean Value Theorem |
|---|---|---|
| Condition | \( f(a) = f(b) \) | No such condition |
| Result | \( f'(c) = 0 \) | \( f'(c) = \dfrac{f(b) – f(a)}{b – a} \) |
| Special Case | MVT when \( f(a) = f(b) \) | General form |
Geometric Comparison
- Rolle’s Theorem: Tangent is horizontal (slope = 0) at some point.
- MVT: Tangent is parallel to the secant line joining \( (a, f(a)) \) and \( (b, f(b)) \).
Practical Uses in JEE
- Used to prove inequalities involving functions.
- Applied in error analysis and motion-related calculus problems.
- Helps in verifying intermediate results (e.g., sign changes, zero slopes).
- Foundation for Taylor’s theorem and Lagrange’s form of remainder.
Key Takeaways
- Check continuity and differentiability before applying these theorems.
- Rolle’s theorem is a special case of the Mean Value Theorem when \( f(a) = f(b) \).
- Both theorems guarantee the existence of at least one point \( c \) — not necessarily unique.
- Always specify \( c \in (a, b) \), not at endpoints.
Common Mistakes to Avoid
- Forgetting to check differentiability (especially at corners or cusps).
- Applying Rolle’s theorem when \( f(a) \ne f(b) \).
- Taking \( c = a \) or \( c = b \) — must lie strictly between the endpoints.
- Ignoring discontinuities (e.g., piecewise or absolute value functions).
Example
Verify Rolle’s theorem for \( f(x) = x^2 – 4x + 3 \) on the interval [1, 3].
▶️ Answer / Explanation
Step 1: \( f(x) = x^2 – 4x + 3 \) is a polynomial ⇒ continuous and differentiable everywhere.
Step 2: \( f(1) = 0, \; f(3) = 0 \Rightarrow f(a) = f(b) \).
Step 3: \( f'(x) = 2x – 4 \Rightarrow f'(c) = 0 \Rightarrow 2c – 4 = 0 \Rightarrow c = 2 \).
Conclusion: All conditions satisfied; \( c = 2 \) satisfies \( f'(c) = 0 \).
Answer: Rolle’s theorem verified with \( c = 2 \).
Example
Check the validity of MVT for \( f(x) = x^2 + 2x + 1 \) on [1, 3] and find the value of \( c \).
▶️ Answer / Explanation
Step 1: \( f(x) = (x + 1)^2 \) is continuous and differentiable everywhere.
Step 2: MVT applies. \( f'(x) = 2x + 2 \).
Step 3: Average rate of change: \( \dfrac{f(3) – f(1)}{3 – 1} = \dfrac{16 – 4}{2} = 6 \).
Now, set \( f'(c) = 6 \Rightarrow 2c + 2 = 6 \Rightarrow c = 2 \).
Answer: \( c = 2 \) satisfies the MVT.
Example
Verify Rolle’s theorem for \( f(x) = \sin 2x \) on \( [0, \pi] \).
▶️ Answer / Explanation
Step 1: \( f(x) = \sin 2x \) is continuous and differentiable on all \( \mathbb{R} \).
Step 2: \( f(0) = \sin 0 = 0, \; f(\pi) = \sin 2\pi = 0 \Rightarrow f(a) = f(b) \).
Step 3: \( f'(x) = 2\cos 2x \).
Set \( f'(c) = 0 \Rightarrow \cos 2c = 0 \Rightarrow 2c = \dfrac{\pi}{2}, \dfrac{3\pi}{2} \Rightarrow c = \dfrac{\pi}{4}, \dfrac{3\pi}{4} \).
Answer: Rolle’s theorem verified; \( c = \dfrac{\pi}{4}, \dfrac{3\pi}{4} \) satisfy \( f'(c) = 0 \).
