IIT JEE Main Maths -Unit 7- Monotonicity- Study Notes-New Syllabus
IIT JEE Main Maths -Unit 7- Monotonicity – Study Notes – New syllabus
IIT JEE Main Maths -Unit 7- Monotonicity – Study Notes -IIT JEE Main Maths – per latest Syllabus.
Key Concepts:
- Applications of Derivatives — Increasing & Decreasing Functions, and Monotonicity
Applications of Derivatives — Increasing & Decreasing Functions, and Monotonicity
Derivatives help us determine where a function is increasing or decreasing. These concepts describe the monotonic behavior of a function — how it changes over its domain.
Let \( y = f(x) \). Then, \( \dfrac{dy}{dx} = f'(x) \) represents the rate of change of \( y \) with respect to \( x \).
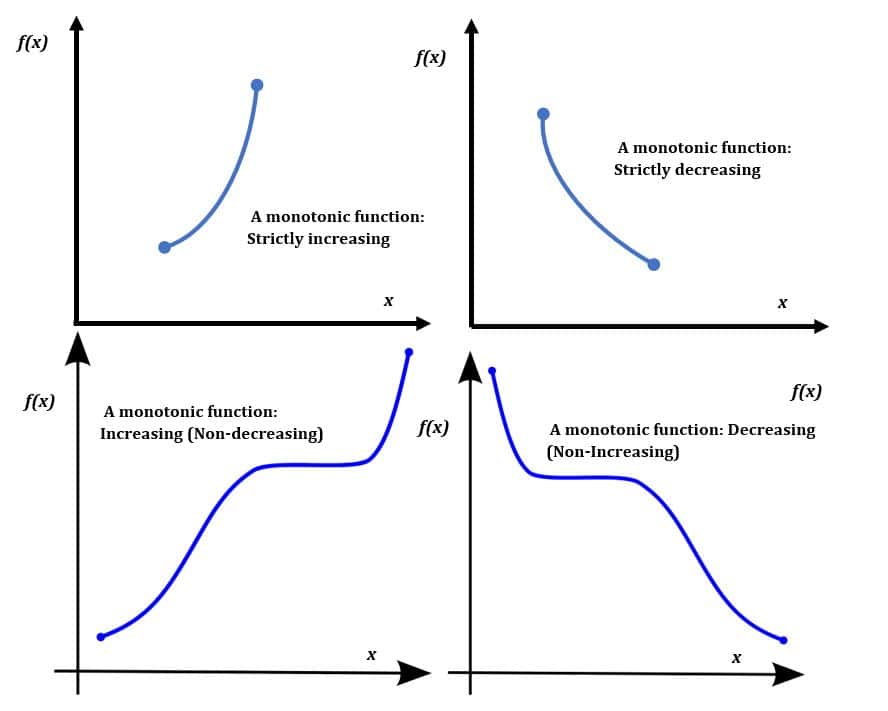
Definition
- A function \( f(x) \) is said to be increasing in an interval \( I \) if: $ \text{for any } x_1 < x_2 \text{ in } I, \; f(x_1) < f(x_2) $
- A function \( f(x) \) is said to be decreasing in an interval \( I \) if: $ \text{for any } x_1 < x_2 \text{ in } I, \; f(x_1) > f(x_2) $
Test Using Derivative
The sign of \( f'(x) \) determines whether \( f(x) \) is increasing or decreasing:
| Condition on \( f'(x) \) | Behavior of \( f(x) \) |
|---|---|
| \( f'(x) > 0 \) | Function is Increasing |
| \( f'(x) < 0 \) | Function is Decreasing |
| \( f'(x) = 0 \) | Stationary Point (Possible Max/Min) |
Steps to Determine Monotonic Intervals
- Find \( f'(x) \).
- Find the points where \( f'(x) = 0 \) or \( f'(x) \) is undefined — these divide the domain into intervals.
- Check the sign of \( f'(x) \) in each interval.
- Positive sign ⇒ Increasing, Negative sign ⇒ Decreasing.
Important Terms
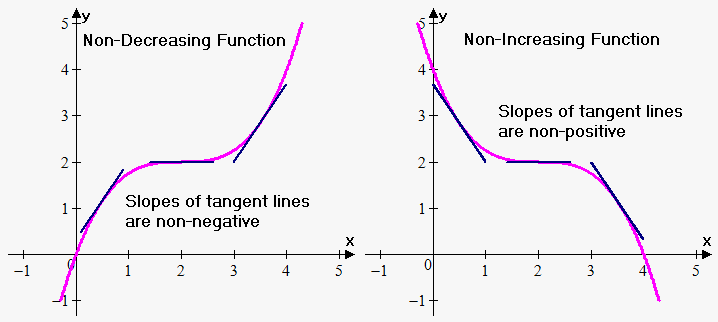
- Monotonic Function: A function that is entirely increasing or decreasing in its domain.
- Strictly Increasing: \( f'(x) > 0 \) for all \( x \) in the interval.
- Strictly Decreasing: \( f'(x) < 0 \) for all \( x \) in the interval.
- Constant Function: \( f'(x) = 0 \).
Graphical Meaning of Monotonicity
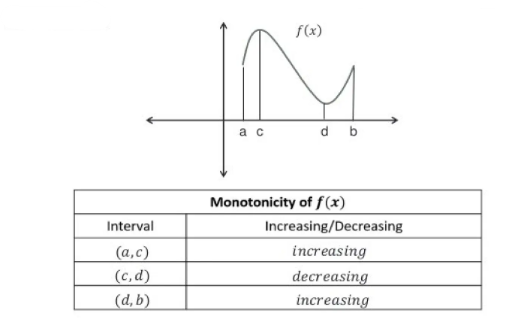
- If \( f'(x) > 0 \): tangent to the curve slopes upward — function rises from left to right.
- If \( f'(x) < 0 \): tangent slopes downward — function falls from left to right.
- If \( f'(x) = 0 \): horizontal tangent — stationary point.
Visualization: An increasing function has a rising graph; a decreasing one slopes downward.
Monotonicity Test Summary
| \( f'(x) \) | Nature of Function | Graph Behavior |
|---|---|---|
| Positive | Increasing | Slopes upward |
| Negative | Decreasing | Slopes downward |
| Zero | Stationary Point | Horizontal tangent |
Example
Find the intervals where \( f(x) = x^2 – 4x + 3 \) is increasing or decreasing.
▶️ Answer / Explanation
\( f'(x) = 2x – 4 = 2(x – 2) \).
\( f'(x) = 0 \Rightarrow x = 2 \).
Check intervals:
- For \( x < 2 \): \( f'(x) < 0 \) → Decreasing.
- For \( x > 2 \): \( f'(x) > 0 \) → Increasing.
Answer: Decreasing on \( (-\infty, 2) \); Increasing on \( (2, \infty) \).
Example
Determine where \( f(x) = \sin x \) is increasing and decreasing on \( [0, 2\pi] \).
▶️ Answer / Explanation
\( f'(x) = \cos x \).
\( f'(x) = 0 \) when \( \cos x = 0 \Rightarrow x = \dfrac{\pi}{2}, \dfrac{3\pi}{2} \).
Check signs:
- \( 0 < x < \dfrac{\pi}{2} \): \( f'(x) > 0 \) → Increasing
- \( \dfrac{\pi}{2} < x < \dfrac{3\pi}{2} \): \( f'(x) < 0 \) → Decreasing
- \( \dfrac{3\pi}{2} < x < 2\pi \): \( f'(x) > 0 \) → Increasing
Answer: Increasing on \( (0, \dfrac{\pi}{2}) \) and \( (\dfrac{3\pi}{2}, 2\pi) \); Decreasing on \( (\dfrac{\pi}{2}, \dfrac{3\pi}{2}) \).
Example
Find intervals of increase and decrease for \( f(x) = \dfrac{x}{x^2 + 1} \).
▶️ Answer / Explanation
\( f'(x) = \dfrac{(x^2 + 1)(1) – x(2x)}{(x^2 + 1)^2} = \dfrac{1 – x^2}{(x^2 + 1)^2} \).
\( f'(x) = 0 \Rightarrow x = \pm 1 \).
Check signs of numerator \( (1 – x^2) \):
- For \( |x| < 1 \): \( 1 – x^2 > 0 \) → Increasing.
- For \( |x| > 1 \): \( 1 – x^2 < 0 \) → Decreasing.
Answer: Increasing on \( (-1, 1) \); Decreasing on \( (-\infty, -1) \cup (1, \infty) \).
