IIT JEE Main Maths -Unit 7- Rate of change- Study Notes-New Syllabus
IIT JEE Main Maths -Unit 7- Rate of change – Study Notes – New syllabus
IIT JEE Main Maths -Unit 7- Rate of change – Study Notes -IIT JEE Main Maths – per latest Syllabus.
Key Concepts:
- Applications of Derivatives — Rate of Change of Quantities
Applications of Derivatives — Rate of Change of Quantities
The rate of change of one quantity with respect to another is a fundamental application of derivatives. It measures how fast one variable changes as another variable changes.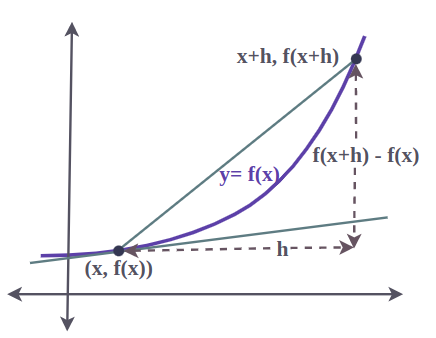
If \( y = f(x) \), then:
$ \text{Rate of change of } y \text{ w.r.t. } x = \dfrac{dy}{dx} $
The derivative \( \dfrac{dy}{dx} \) gives the instantaneous rate of change of \( y \) when \( x \) changes by an infinitesimally small amount.
Physical Interpretation
- In physics, \( \dfrac{ds}{dt} \) represents velocity (rate of change of displacement).
- \( \dfrac{dv}{dt} \) represents acceleration (rate of change of velocity).
- In geometry, \( \dfrac{dA}{dt} \) may represent the rate at which the area of a figure changes over time.
Thus, derivatives act as tools to measure how fast quantities vary in real-world problems.
Formula Recap
| Quantity | Derivative Meaning |
|---|---|
| \( \dfrac{ds}{dt} \) | Velocity (rate of change of position) |
| \( \dfrac{dv}{dt} \) | Acceleration (rate of change of velocity) |
| \( \dfrac{dA}{dt} \) | Rate of change of area |
| \( \dfrac{dV}{dt} \) | Rate of change of volume |
Method to Solve “Rate of Change” Problems
- Identify the two variables involved (e.g., \( x, y \)).
- Find the relation between them (geometric, physical, etc.).
- Differentiate both sides with respect to time \( t \).
- Substitute known values and solve for the required rate (e.g., \( \dfrac{dy}{dt} \)).
Example
The radius of a circle increases at a rate of \( 2 \, \text{cm/s} \). Find the rate of increase of its area when the radius is \( 7 \, \text{cm} \).
▶️ Answer / Explanation
Given: \( \dfrac{dr}{dt} = 2 \, \text{cm/s} \), \( r = 7 \, \text{cm} \).
Area of circle: \( A = \pi r^2 \).
Differentiating both sides w.r.t. \( t \):
\( \dfrac{dA}{dt} = 2\pi r \dfrac{dr}{dt} \).
Substitute values: \( \dfrac{dA}{dt} = 2\pi(7)(2) = 28\pi \, \text{cm}^2/\text{s} \).
Answer: \( 28\pi \, \text{cm}^2/\text{s} \)
Example
A balloon is rising vertically at a rate of \( 4 \, \text{m/s} \). A man is standing \( 10 \, \text{m} \) away from the point on the ground directly below the balloon. How fast is the distance between the man and the balloon increasing when the balloon is \( 15 \, \text{m} \) above the ground?
▶️ Answer / Explanation
Let \( y \) be the height of the balloon, and \( s \) be the distance between the man and the balloon.
Given: \( \dfrac{dy}{dt} = 4 \, \text{m/s}, \, y = 15 \, \text{m} \), horizontal distance = 10 m.
From Pythagoras: \( s^2 = y^2 + 10^2 \).
Differentiating both sides w.r.t. \( t \): \( 2s\dfrac{ds}{dt} = 2y\dfrac{dy}{dt} \).
\( \Rightarrow \dfrac{ds}{dt} = \dfrac{y}{s}\dfrac{dy}{dt} \).
When \( y = 15 \), \( s = \sqrt{15^2 + 10^2} = \sqrt{325} = 5\sqrt{13} \).
\( \Rightarrow \dfrac{ds}{dt} = \dfrac{15}{5\sqrt{13}}(4) = \dfrac{12}{\sqrt{13}} \, \text{m/s} \).
Answer: \( \dfrac{12}{\sqrt{13}} \, \text{m/s} \)
Example
Water is leaking out of a conical tank at a rate of \( 2 \, \text{cm}^3/\text{s} \). The height of the tank is \( 24 \, \text{cm} \) and the radius at the top is \( 6 \, \text{cm} \). Find the rate at which the water level is falling when the water depth is \( 4 \, \text{cm} \).
▶️ Answer / Explanation
Let \( r \) = radius of water surface, \( h \) = depth of water, \( V = \dfrac{1}{3}\pi r^2h \).
Given: \( \dfrac{dV}{dt} = -2 \, \text{cm}^3/\text{s} \).
From geometry of cone: \( \dfrac{r}{h} = \dfrac{6}{24} = \dfrac{1}{4} \Rightarrow r = \dfrac{h}{4} \).
Substitute in \( V \): \( V = \dfrac{1}{3}\pi \left(\dfrac{h}{4}\right)^2h = \dfrac{\pi h^3}{48} \).
Differentiating w.r.t. \( t \): \( \dfrac{dV}{dt} = \dfrac{\pi}{16} h^2 \dfrac{dh}{dt} \).
\( \Rightarrow \dfrac{dh}{dt} = \dfrac{16}{\pi h^2} \dfrac{dV}{dt} \).
Substitute \( h = 4, \, \dfrac{dV}{dt} = -2 \): \( \dfrac{dh}{dt} = \dfrac{16}{\pi (16)}(-2) = -\dfrac{2}{\pi} \, \text{cm/s} \).
Answer: The water level is falling at \( \dfrac{2}{\pi} \, \text{cm/s} \).
