IIT JEE Main Maths -Unit 7- Real-valued functions and types- Study Notes-New Syllabus
IIT JEE Main Maths -Unit 7- Real-valued functions and types – Study Notes – New syllabus
IIT JEE Main Maths -Unit 7- Real-valued functions and types – Study Notes -IIT JEE Main Maths – per latest Syllabus.
Key Concepts:
- Real-Valued Functions and Their Types
- Domain and Range of Real-Valued Functions
Real-Valued Functions and Their Types
A function is a special type of relation where each element in the domain is associated with exactly one element in the co-domain.
$ f: A \to B \text{ is a function if for every } a \in A, \text{ there exists exactly one } b \in B \text{ such that } f(a) = b. $
Here,
- Domain: Set of all possible input values.
- Co-domain: Set from which output values are taken.
- Range: Set of all actual output values.
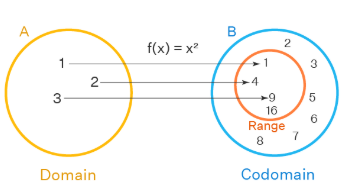
Real-Valued Function
A function \( f \) is called a real-valued function if:
$ f: A \to \mathbb{R}, \quad \text{where both domain and range are subsets of } \mathbb{R}. $
That means both inputs and outputs are real numbers.
Examples: $ f(x) = 2x + 3, \quad g(x) = x^2 – 5x + 6, \quad h(x) = \sqrt{x} $
Representation of a Function
- Verbal Form: e.g., “Square each real number.”
- Algebraic Form: \( f(x) = x^2 \).
- Graphical Form: Plot of ordered pairs \( (x, f(x)) \) on the Cartesian plane.
- Tabular Form: Function values for discrete inputs.
Types of Real-Valued Functions (JEE Classification)
Real-valued functions are classified based on their algebraic form and behavior:
(a) Polynomial Functions
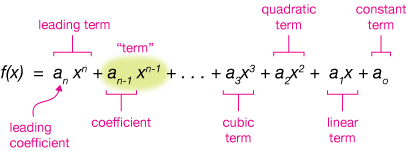
A function of the form $ f(x) = a_0 + a_1x + a_2x^2 + \dots + a_nx^n $ where \( a_i \) are real constants and \( n \) is a non-negative integer.
Examples: \( f(x) = 3x^2 + 2x + 1, \quad g(x) = x^3 – 7x \)
(b) Rational Functions
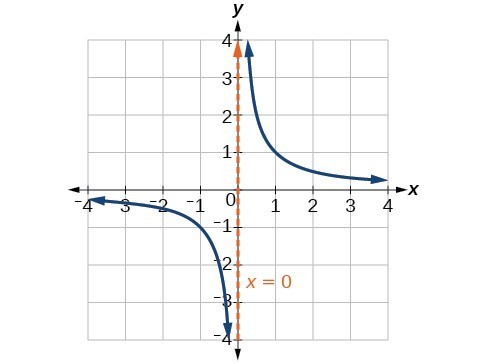
Quotient of two polynomial functions.
$ f(x) = \dfrac{p(x)}{q(x)}, \quad \text{where } q(x) \ne 0 $
Example: \( f(x) = \dfrac{x^2 + 1}{x – 2} \)
Domain: All real \( x \ne 2 \).
(c) Irrational (Radical) Functions
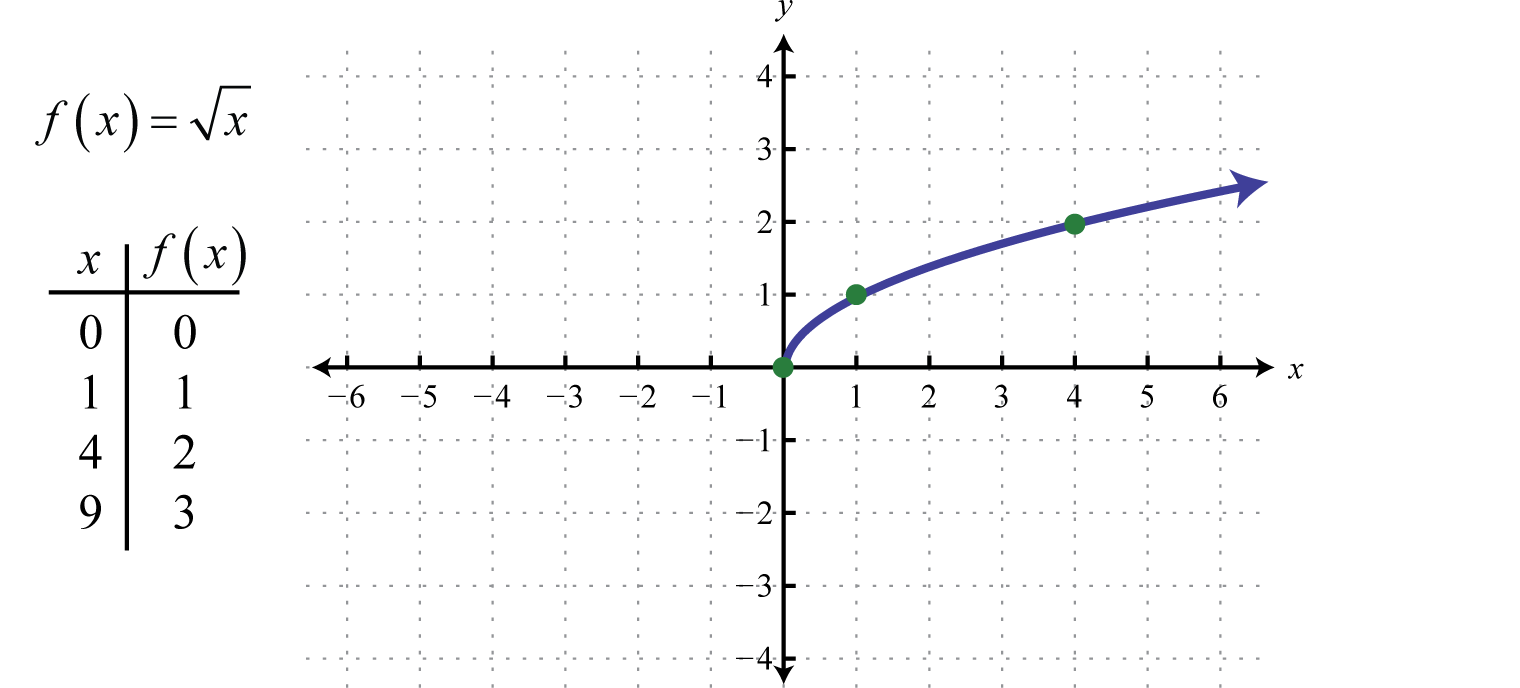
Contain roots of polynomials.
$ f(x) = \sqrt{x}, \quad f(x) = \sqrt{x^2 + 1}, \quad f(x) = \sqrt{1 – x} $
Domain restriction: Expression inside the root must be non-negative.
(d) Modulus (Absolute Value) Function
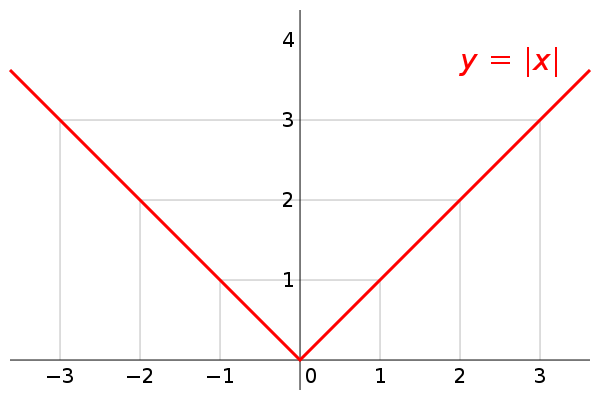
Defined as $ f(x) = |x| = \begin{cases} x, & x \ge 0 \\ -x, & x < 0 \end{cases} $
Graph: V-shaped curve symmetric about the y-axis.
(e) Greatest Integer Function (GIF or Floor Function)
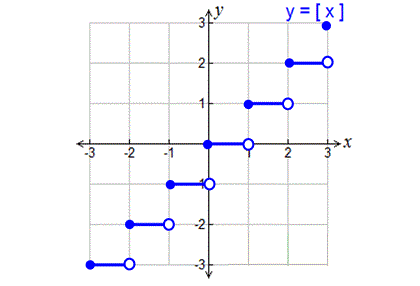
Defined as $ f(x) = [x] $ where [x] denotes the greatest integer less than or equal to x.
Examples: \([2.3] = 2, \, [-2.3] = -3\)
(f) Fractional Part Function
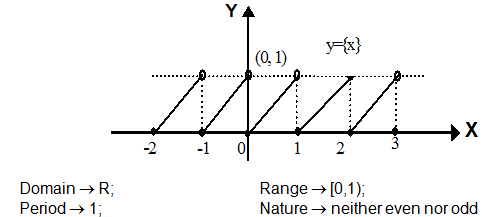
Defined as $ f(x) = x – [x] $
It gives the fractional part of \( x \). \(\text{Example: } f(3.7) = 0.7, \, f(-2.3) = 0.7\)
(g) Exponential Function
Defined as $ f(x) = a^x, \quad a > 0, a \ne 1 $
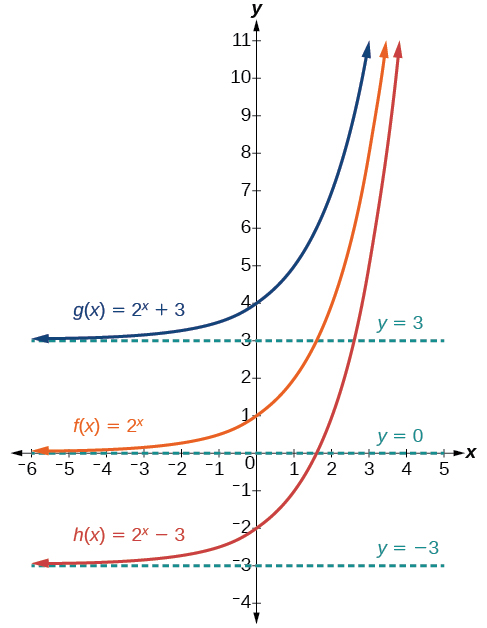
Examples: \( f(x) = 2^x, \, e^x, \, 10^x \)
Range: \( (0, \infty) \)
(h) Logarithmic Function
Inverse of exponential function.
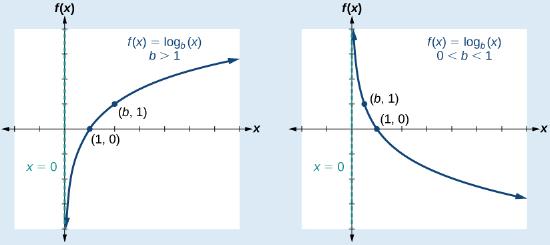
$ f(x) = \log_a x, \quad a > 0, a \ne 1 $
Domain: \( x > 0 \), Range: All real numbers.
(i) Trigonometric Functions
Based on angle measurements. $ \sin x, \cos x, \tan x, \cot x, \sec x, \csc x $

Defined for all real \( x \) (except points where denominator = 0).
(j) Inverse Trigonometric Functions
Inverse of trigonometric functions with restricted domains.
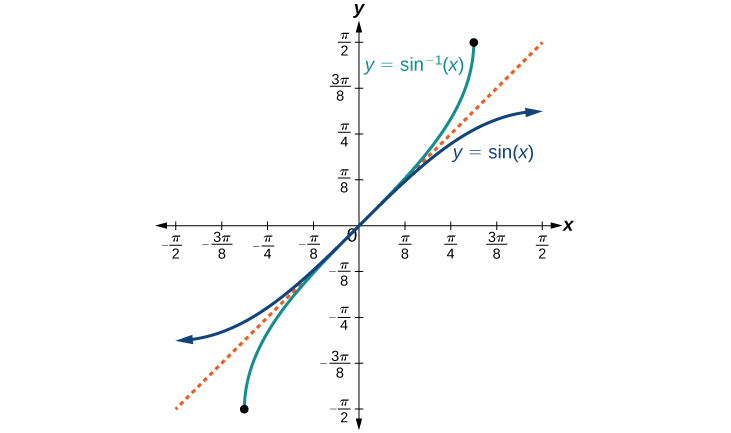
Examples:
- \( y = \sin^{-1}x, \quad x \in [-1, 1] \)
- \( y = \tan^{-1}x, \quad x \in \mathbb{R} \)
(k) Piecewise Defined Functions
Defined by different expressions in different intervals of the domain.
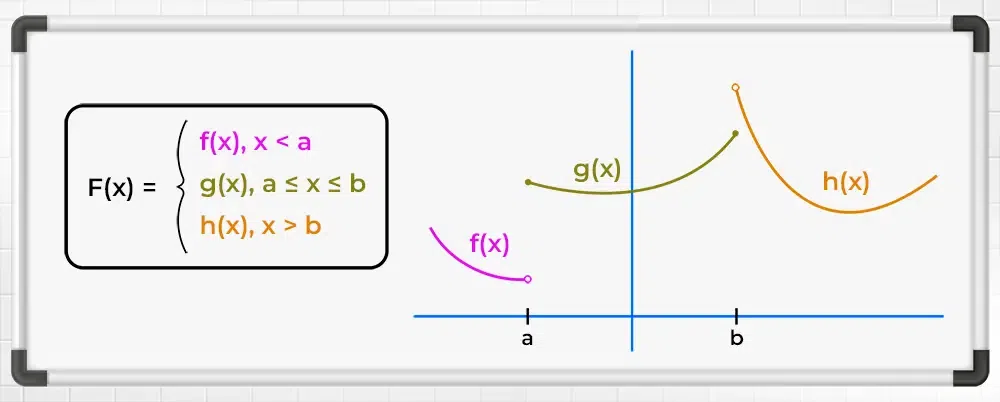
Example:
$ f(x) = \begin{cases} x^2, & x \le 0 \\ x + 1, & x > 0 \end{cases} $
Example
Find the domain and range of \( f(x) = \sqrt{x – 3} \).
▶️ Answer / Explanation
For square root to be real, \( x – 3 \ge 0 \Rightarrow x \ge 3 \).
Domain: \( [3, \infty) \)
Range: \( [0, \infty) \)
Example
Find the domain and range of \( f(x) = \dfrac{1}{x^2 – 4} \).
▶️ Answer / Explanation
Denominator ≠ 0 ⇒ \( x^2 – 4 ≠ 0 ⇒ x ≠ ±2 \).
Domain: \( \mathbb{R} – \{-2, 2\} \)
Range: \( (-\infty, -\dfrac{1}{4}] \cup (0, \infty) \)
Example
Find the domain of \( f(x) = \log(\sqrt{x^2 – 4}) \).
▶️ Answer / Explanation
For log function, argument > 0 ⇒ \( \sqrt{x^2 – 4} > 0 ⇒ x^2 – 4 > 0 \).
⇒ \( x < -2 \) or \( x > 2 \).
Domain: \( (-\infty, -2) \cup (2, \infty) \)
Domain and Range of Real-Valued Functions
For a real-valued function \( f: A \to \mathbb{R} \):
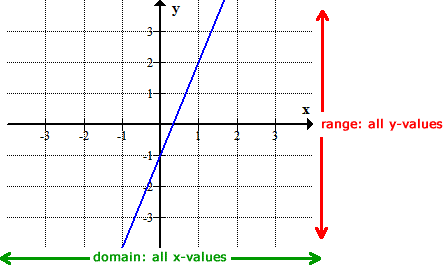
- Domain: The set of all real values of \( x \) for which \( f(x) \) is defined (real).
- Range: The set of all possible real values taken by \( f(x) \).
Basic Rules to Find Domain
When finding the domain of \( f(x) \), ensure that all operations in the function are valid for real numbers.
| Type of Expression | Condition for Real Domain | Example |
|---|---|---|
| Square root / Even root | Expression inside ≥ 0 | \( \sqrt{x – 3} \Rightarrow x \ge 3 \) |
| Denominator | Denominator ≠ 0 | \( \dfrac{1}{x – 2} \Rightarrow x \ne 2 \) |
| Logarithm | Argument > 0 | \( \log(x – 1) \Rightarrow x > 1 \) |
| Even root inside log | Expression inside root > 0 | \( \log(\sqrt{x – 4}) \Rightarrow x > 4 \) |
| Inverse Trigonometric | Argument lies in valid range | \( \sin^{-1}x \Rightarrow -1 \le x \le 1 \) |
Techniques to Find Range
Once the domain is found, use one of these techniques to determine the range:
- Direct substitution: For simple polynomial functions.
- Transformation method: For shifted/scaled functions using base graphs.
- Substitution (inverse approach): Express \( x \) in terms of \( y \) and find possible \( y \) values.
- Using inequalities: For rational, square root, and trigonometric functions.
Domain and Range of Common Functions
| Function | Domain | Range |
|---|---|---|
| \( f(x) = x^2 \) | \( \mathbb{R} \) | \( [0, \infty) \) |
| \( f(x) = \sqrt{x} \) | \( [0, \infty) \) | \( [0, \infty) \) |
| \( f(x) = \dfrac{1}{x} \) | \( \mathbb{R} – \{0\} \) | \( \mathbb{R} – \{0\} \) |
| \( f(x) = e^x \) | \( \mathbb{R} \) | \( (0, \infty) \) |
| \( f(x) = \log x \) | \( (0, \infty) \) | \( \mathbb{R} \) |
| \( f(x) = \sin x \) | \( \mathbb{R} \) | \( [-1, 1] \) |
Example
Find the domain and range of \( f(x) = \sqrt{4 – x^2} \).
▶️ Answer / Explanation
Expression inside root ≥ 0 ⇒ \( 4 – x^2 \ge 0 \Rightarrow -2 \le x \le 2 \).
For \( x = -2 \) or \( 2 \), \( f(x) = 0 \); for \( x = 0 \), \( f(0) = 2 \).
Domain: \( [-2, 2] \)
Range: \( [0, 2] \)
Example
Find the domain and range of \( f(x) = \dfrac{1}{x^2 – 2x – 3} \).
▶️ Answer / Explanation
Denominator ≠ 0 ⇒ \( x^2 – 2x – 3 ≠ 0 \Rightarrow (x – 3)(x + 1) ≠ 0 \Rightarrow x \ne 3, -1 \).
Domain: \( \mathbb{R} – \{-1, 3\} \)
Range can be found by substituting \( y = \dfrac{1}{x^2 – 2x – 3} \) ⇒ \( x^2 – 2x – 3 = \dfrac{1}{y} \) ⇒ \( x^2 – 2x – (3 + \dfrac{1}{y}) = 0 \).
For real \( x \), discriminant ≥ 0 ⇒ \( 4 + 4(3 + \dfrac{1}{y}) \ge 0 \Rightarrow y \le -\dfrac{1}{4} \text{ or } y > 0 \).
Range: \( (-\infty, -\dfrac{1}{4}] \cup (0, \infty) \)
Example
Find the domain and range of \( f(x) = \log(\sqrt{x^2 – 4}) \).
▶️ Answer / Explanation
Argument of log > 0 ⇒ \( \sqrt{x^2 – 4} > 0 ⇒ x^2 – 4 > 0 ⇒ x < -2 \text{ or } x > 2 \).
Domain: \( (-\infty, -2) \cup (2, \infty) \)
For range, let \( y = \log(\sqrt{x^2 – 4}) = \dfrac{1}{2}\log(x^2 – 4) \).
As \( x^2 – 4 \in (0, \infty) \), \( \log(x^2 – 4) \in (-\infty, \infty) \).
Range: \( (-\infty, \infty) \)
