IIT JEE Main Maths -Unit 8- Fundamental theorem of calculus- Study Notes-New Syllabus
IIT JEE Main Maths -Unit 8- Fundamental theorem of calculus – Study Notes – New syllabus
IIT JEE Main Maths -Unit 8- Fundamental theorem of calculus – Study Notes -IIT JEE Main Maths – per latest Syllabus.
Key Concepts:
- Fundamental Theorem of Calculus
Fundamental Theorem of Calculus
The Fundamental Theorem of Calculus (FTC) connects the two central concepts of calculus: Differentiation and Integration. It provides a direct link between finding the derivative of an integral and the integral of a derivative.
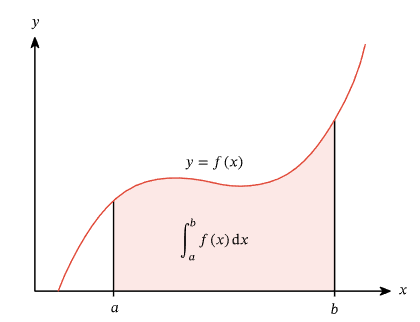
It is divided into two parts — First Fundamental Theorem and Second Fundamental Theorem.
First Fundamental Theorem of Calculus
Statement: If \( f(x) \) is a continuous function on the interval \([a, b]\), and a function \( F(x) \) is defined as
$ F(x) = \int_a^x f(t)\,dt, $
then \( F(x) \) is differentiable on \((a, b)\) and
$ F'(x) = f(x). $
Meaning: Differentiation and integration are inverse operations of each other.
Second Fundamental Theorem of Calculus
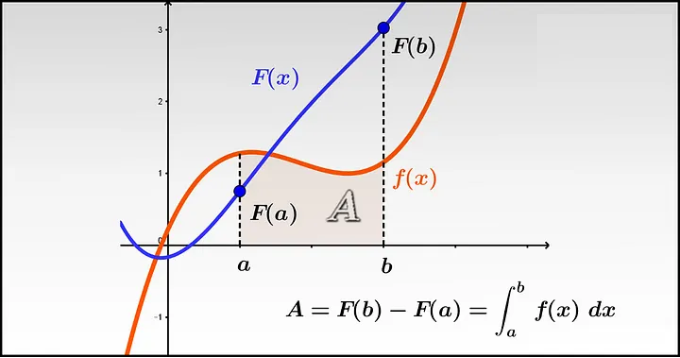
Statement: If \( f(x) \) is continuous on \([a, b]\) and \( F(x) \) is any anti-derivative of \( f(x) \), then
$ \int_a^b f(x)\,dx = F(b) – F(a). $
Meaning: The definite integral of a function between two limits equals the change in its anti-derivative between those limits.
Relation Between Both Theorems
| Aspect | First Fundamental Theorem | Second Fundamental Theorem |
|---|---|---|
| Concept | Differentiation of an integral | Evaluation of a definite integral |
| Formula | \( \dfrac{d}{dx}\int_a^x f(t)\,dt = f(x) \) | \( \int_a^b f(x)\,dx = F(b) – F(a) \) |
| Purpose | Converts integration to differentiation | Converts definite integral to algebraic difference |
Geometrical Interpretation
- The function \( F(x) = \displaystyle \int_a^x f(t)\,dt \) represents the area under the curve \( y = f(t) \) from \( t = a \) to \( t = x \).
- The derivative \( F'(x) = f(x) \) gives the rate of change of this area with respect to \( x \).
Example
If \( F(x) = \displaystyle \int_0^x (t^2 + 1)\,dt \), find \( F'(x) \).
▶️ Answer / Explanation
By the First Fundamental Theorem:
\( F'(x) = f(x) = x^2 + 1. \)
Answer: \( F'(x) = x^2 + 1. \)
Example
Evaluate \( \displaystyle \int_0^3 (2x + 1)\,dx \).
▶️ Answer / Explanation
Step 1: Find anti-derivative \( F(x) = x^2 + x. \)
Step 2: Apply limits 0 to 3: \( F(3) – F(0) = (9 + 3) – 0 = 12. \)
Answer: \( 12. \)
Example
Find \( \dfrac{d}{dx}\left[\displaystyle \int_0^{x^2} \sin t\,dt\right] \).
▶️ Answer / Explanation
By the Leibniz Rule (extended form of FTC):
\( \dfrac{d}{dx}\int_a^{g(x)} f(t)\,dt = f(g(x)) \cdot g'(x). \)
Here, \( f(t) = \sin t \) and \( g(x) = x^2 \).
Thus, \( \dfrac{d}{dx} = \sin(x^2) \cdot 2x = 2x\sin(x^2). \)
Answer: \( 2x\sin(x^2). \)
Leibniz Rule (Generalized Form)
If the limits of integration are both functions of \( x \):
$ \dfrac{d}{dx}\left[\int_{a(x)}^{b(x)} f(t)\,dt\right] = f(b(x))\,b'(x) – f(a(x))\,a'(x) $
Example
Find \( \dfrac{d}{dx}\left[\displaystyle \int_{\sin x}^{x^2} e^{t^2}\,dt\right] \).
▶️ Answer / Explanation
Apply the Leibniz Rule:
\( f(t) = e^{t^2}, \, a(x) = \sin x, \, b(x) = x^2. \)
\( \Rightarrow \dfrac{d}{dx} = f(b(x))b'(x) – f(a(x))a'(x). \)
\( = e^{(x^2)^2} \cdot 2x – e^{(\sin x)^2}\cdot \cos x. \)
Answer: \( 2x e^{x^4} – \cos x\,e^{\sin^2x}. \)
