IIT JEE Main Maths -Unit 8- Methods of integration: substitution, parts, partial fractions- Study Notes-New Syllabus
IIT JEE Main Maths -Unit 8- Methods of integration: substitution, parts, partial fractions – Study Notes – New syllabus
IIT JEE Main Maths -Unit 8- Methods of integration: substitution, parts, partial fractions – Study Notes -IIT JEE Main Maths – per latest Syllabus.
Key Concepts:
- Methods of Integration — Substitution Method
- Methods of Integration — Partial Fractions
- Methods of Integration — Integration by Parts (ILATE Rule)
Methods of Integration — Substitution Method
The Substitution Method is used when an integral can be simplified by changing the variable of integration. It is based on the chain rule of differentiation in reverse.
If \( x = g(t) \), then \( dx = g'(t)\,dt \), and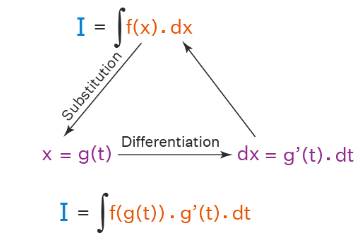
$ \int f(g(x))\,g'(x)\,dx = \int f(t)\,dt $
This change of variable helps convert a complicated function into a simpler form that matches a standard integral.
Formula (Change of Variable Rule)
If \( x = g(t) \), then:
$ \int f(x)\,dx = \int f(g(t))\,g'(t)\,dt $
After integration, replace \( t \) by \( x \) again (back-substitution).
Steps in Substitution Method
- Identify the inner function \( g(x) \) whose derivative also appears in the integrand.
- Let \( t = g(x) \) → compute \( dt = g'(x)\,dx \).
- Rewrite the integral entirely in terms of \( t \) and \( dt \).
- Integrate with respect to \( t \).
- Substitute back \( t = g(x) \) in the final result.
Important Substitution Patterns
| Type of Function | Substitute |
|---|---|
| \( f(ax + b) \) | Let \( t = ax + b \) |
| \( x^2 + a^2 \), \( x^2 – a^2 \), or \( a^2 – x^2 \) | Use trigonometric substitution |
| \( e^{g(x)} \) or \( \sin(g(x)) \) | Let \( t = g(x) \) |
Example
Evaluate \( \displaystyle \int (3x + 5)^2\,dx \).
▶️ Answer / Explanation
Step 1: Let \( t = 3x + 5 \Rightarrow dt = 3\,dx \Rightarrow dx = \dfrac{dt}{3} \).
Step 2: Substitute into the integral:
\( \displaystyle \int (3x + 5)^2\,dx = \int t^2 \cdot \dfrac{dt}{3} = \dfrac{1}{3}\int t^2\,dt \).
Step 3: Integrate: \( \dfrac{1}{3} \cdot \dfrac{t^3}{3} = \dfrac{t^3}{9} + C \).
Step 4: Substitute back \( t = 3x + 5 \): \( \displaystyle \dfrac{(3x + 5)^3}{9} + C \).
Answer: \( \dfrac{(3x + 5)^3}{9} + C \).
Example
Evaluate \( \displaystyle \int x e^{x^2}\,dx \).
▶️ Answer / Explanation
Step 1: Let \( t = x^2 \Rightarrow dt = 2x\,dx \Rightarrow x\,dx = \dfrac{dt}{2} \).
Step 2: Substitute: \( \displaystyle \int x e^{x^2}\,dx = \int e^t \cdot \dfrac{dt}{2} = \dfrac{1}{2}\int e^t\,dt \).
Step 3: Integrate: \( \dfrac{1}{2}e^t + C \).
Step 4: Back-substitute \( t = x^2 \): \( \displaystyle \dfrac{1}{2}e^{x^2} + C \).
Answer: \( \dfrac{1}{2}e^{x^2} + C \).
Example
Evaluate \( \displaystyle \int \dfrac{dx}{\sqrt{a^2 – x^2}} \).
▶️ Answer / Explanation
Step 1: Let \( x = a\sin\theta \Rightarrow dx = a\cos\theta\,d\theta \).
Step 2: Substitute into the integral:
\( \displaystyle \int \dfrac{dx}{\sqrt{a^2 – x^2}} = \int \dfrac{a\cos\theta\,d\theta}{\sqrt{a^2 – a^2\sin^2\theta}} = \int \dfrac{a\cos\theta\,d\theta}{a\cos\theta} = \int d\theta \).
Step 3: Integrate: \( \theta + C \).
Step 4: Back-substitute \( \theta = \sin^{-1}\left(\dfrac{x}{a}\right) \).
Answer: \( \sin^{-1}\left(\dfrac{x}{a}\right) + C \).
Special Trigonometric Substitutions
| Expression | Substitution |
|---|---|
| \( \sqrt{a^2 – x^2} \) | Let \( x = a\sin\theta \) |
| \( \sqrt{a^2 + x^2} \) | Let \( x = a\tan\theta \) |
| \( \sqrt{x^2 – a^2} \) | Let \( x = a\sec\theta \) |
Methods of Integration — Partial Fractions
The Partial Fractions Method is used to integrate rational functions, i.e., expressions of the form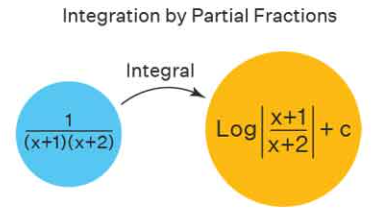
$ \dfrac{P(x)}{Q(x)} $
where both \( P(x) \) and \( Q(x) \) are polynomials and the degree of \( P(x) \) is less than the degree of \( Q(x) \).
This method involves expressing the rational function as a sum of simpler fractions, called partial fractions, whose integrals are standard forms.
Basic Condition
Before using partial fractions, ensure that:
- The degree of numerator < \( \) degree of denominator.
- If not, perform polynomial long division first.
Types of Denominators and Their Decompositions
| Type of Denominator | Partial Fraction Form |
|---|---|
| Distinct linear factors: \( (x – a)(x – b) \) | \( \dfrac{A}{x – a} + \dfrac{B}{x – b} \) |
| Repeated linear factor: \( (x – a)^2 \) | \( \dfrac{A}{x – a} + \dfrac{B}{(x – a)^2} \) |
| Irreducible quadratic: \( x^2 + bx + c \) | \( \dfrac{Ax + B}{x^2 + bx + c} \) |
| Repeated quadratic: \( (x^2 + bx + c)^2 \) | \( \dfrac{Ax + B}{x^2 + bx + c} + \dfrac{Cx + D}{(x^2 + bx + c)^2} \) |
General Procedure
- Ensure the degree of numerator < denominator (if not, divide).
- Factorize the denominator completely.
- Write the proper partial fraction form.
- Multiply through by the denominator to eliminate fractions.
- Compare coefficients or substitute convenient values to find constants.
- Integrate each term separately using standard formulas.
Example
Evaluate \( \displaystyle \int \dfrac{2x + 3}{(x + 1)(x + 2)}\,dx \).
▶️ Answer / Explanation
Step 1: Write as \( \dfrac{2x + 3}{(x + 1)(x + 2)} = \dfrac{A}{x + 1} + \dfrac{B}{x + 2} \).
Step 2: Multiply both sides by \( (x + 1)(x + 2) \): \( 2x + 3 = A(x + 2) + B(x + 1) \).
Substitute \( x = -1 \Rightarrow 2(-1) + 3 = A(1) \Rightarrow A = 1. \)
Substitute \( x = -2 \Rightarrow 2(-2) + 3 = B(-1) \Rightarrow B = 1. \)
Step 3: Integral becomes \( \displaystyle \int \left( \dfrac{1}{x + 1} + \dfrac{1}{x + 2} \right)\,dx \).
Step 4: Integrate: \( \ln|x + 1| + \ln|x + 2| + C = \ln|(x + 1)(x + 2)| + C \).
Answer: \( \ln|(x + 1)(x + 2)| + C \).
Example
Evaluate \( \displaystyle \int \dfrac{3x + 1}{(x + 2)^2}\,dx \).
▶️ Answer / Explanation
Step 1: Write as \( \dfrac{3x + 1}{(x + 2)^2} = \dfrac{A}{x + 2} + \dfrac{B}{(x + 2)^2} \).
Step 2: Multiply by \( (x + 2)^2 \): \( 3x + 1 = A(x + 2) + B \).
Expand: \( 3x + 1 = Ax + 2A + B \).
Compare coefficients: \( 3 = A \), \( 1 = 2A + B \Rightarrow B = -5. \)
Step 3: Substitute: \( \displaystyle \int \left( \dfrac{3}{x + 2} – \dfrac{5}{(x + 2)^2} \right)\,dx \).
Step 4: Integrate: \( 3\ln|x + 2| + \dfrac{5}{x + 2} + C \).
Answer: \( 3\ln|x + 2| + \dfrac{5}{x + 2} + C \).
Example
Evaluate \( \displaystyle \int \dfrac{2x + 3}{x^2 + 4x + 5}\,dx \).
▶️ Answer / Explanation
Step 1: Complete the square in denominator: \( x^2 + 4x + 5 = (x + 2)^2 + 1 \).
Step 2: Split numerator: \( 2x + 3 = 2(x + 2) – 1 \).
Step 3: Separate integral: \( \displaystyle \int \dfrac{2(x + 2)}{(x + 2)^2 + 1}\,dx – \int \dfrac{1}{(x + 2)^2 + 1}\,dx \).
Step 4: Use standard results: \( \int \dfrac{2u}{u^2 + 1}\,du = \ln(u^2 + 1) \), \( \int \dfrac{1}{u^2 + 1}\,du = \tan^{-1}(u) \).
Step 5: Final answer: \( \ln[(x + 2)^2 + 1] – \tan^{-1}(x + 2) + C \).
Answer: \( \ln[(x + 2)^2 + 1] – \tan^{-1}(x + 2) + C \).
Methods of Integration — Integration by Parts (ILATE Rule)
The Integration by Parts method is used when the integrand is a product of two different types of functions.
It is based on the product rule of differentiation applied in reverse.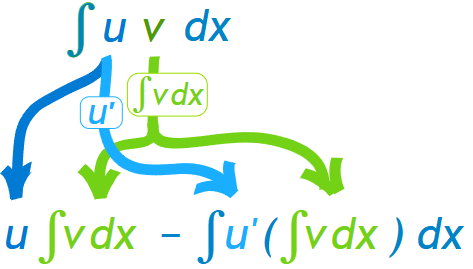
If \( u = u(x) \) and \( v = v(x) \), then
$ \displaystyle \int u\,dv = uv – \int v\,du $
This means that to integrate the product \( u \cdot v’ \), we differentiate \( u \) and integrate \( v’ \).
Formula (Integration by Parts)
$ \boxed{\displaystyle \int u\,dv = u\,v – \int v\,du} $
Here:
- \( u \) = the first function (to be differentiated)
- \( dv \) = the second function (to be integrated)
ILATE Rule — Order of Preference
When choosing which function to take as \( u \) and which as \( dv \), we use the ILATE rule (or sometimes LIATE).
| Priority | Function Type | Examples |
|---|---|---|
| 1 (Highest) | Inverse Trigonometric | \( \sin^{-1}x, \tan^{-1}x \) |
| 2 | Logarithmic | \( \ln x, \log_{10}x \) |
| 3 | Algebraic | \( x, x^2, x^3 \) |
| 4 | Trigonometric | \( \sin x, \cos x, \tan x \) |
| 5 (Lowest) | Exponential | \( e^x, a^x \) |
Steps for Integration by Parts
- Choose \( u \) and \( dv \) according to ILATE priority.
- Find \( du = \dfrac{du}{dx}dx \) and \( v = \int dv \).
- Apply the formula \( \displaystyle \int u\,dv = uv – \int v\,du \).
- Integrate the remaining part \( \int v\,du \).
- Add constant of integration \( C \).
Example
Evaluate \( \displaystyle \int x e^x\,dx \).
▶️ Answer / Explanation
Step 1: According to ILATE — Algebraic first, Exponential second. \( u = x, \, dv = e^x dx. \)
Step 2: Then \( du = dx \), \( v = e^x. \)
Step 3: Apply formula: \( \displaystyle \int x e^x dx = x e^x – \int e^x dx. \)
Step 4: Integrate: \( x e^x – e^x + C. \)
Answer: \( e^x(x – 1) + C. \)
Example
Evaluate \( \displaystyle \int x \ln x\,dx \).
▶️ Answer / Explanation
Step 1: According to ILATE — Logarithmic first, Algebraic second. \( u = \ln x, \, dv = x\,dx. \)
Step 2: Then \( du = \dfrac{1}{x}dx \), \( v = \dfrac{x^2}{2}. \)
Step 3: Apply formula: \( \displaystyle \int x \ln x\,dx = \ln x \cdot \dfrac{x^2}{2} – \int \dfrac{x^2}{2} \cdot \dfrac{1}{x} dx. \)
Step 4: Simplify: \( = \dfrac{x^2}{2}\ln x – \dfrac{1}{2}\int x\,dx = \dfrac{x^2}{2}\ln x – \dfrac{x^2}{4} + C. \)
Answer: \( \dfrac{x^2}{2}(\ln x – \dfrac{1}{2}) + C. \)
Example
Evaluate \( \displaystyle \int x \tan^{-1}x\,dx \).
▶️ Answer / Explanation
Step 1: According to ILATE — Inverse Trig first, Algebraic second. \( u = \tan^{-1}x, \, dv = x\,dx. \)
Step 2: \( du = \dfrac{1}{1 + x^2}dx, \, v = \dfrac{x^2}{2}. \)
Step 3: Apply formula: \( \displaystyle \int x \tan^{-1}x\,dx = \dfrac{x^2}{2}\tan^{-1}x – \int \dfrac{x^2}{2(1 + x^2)}dx. \)
Step 4: Simplify integrand: \( \dfrac{x^2}{1 + x^2} = 1 – \dfrac{1}{1 + x^2} \). So, \( \displaystyle \int \dfrac{x^2}{2(1 + x^2)}dx = \dfrac{1}{2}\int \left(1 – \dfrac{1}{1 + x^2}\right)dx = \dfrac{1}{2}(x – \tan^{-1}x). \)
Step 5: Substitute back: \( \dfrac{x^2}{2}\tan^{-1}x – \dfrac{1}{2}(x – \tan^{-1}x) + C. \)
Answer: \( \dfrac{1}{2}\big[(x^2 + 1)\tan^{-1}x – x\big] + C. \)
