IIT JEE Main Maths -Unit 9- Linear differential equations of type \(\mathrm{\frac{dy}{dx} + P(x)y = Q(x)}\)- Study Notes-New Syllabus
IIT JEE Main Maths -Unit 9- Linear differential equations of type \(\mathrm{\frac{dy}{dx} + P(x)y = Q(x)}\) – Study Notes – New syllabus
IIT JEE Main Maths -Unit 9- Linear differential equations of type \(\mathrm{\frac{dy}{dx} + P(x)y = Q(x)}\) – Study Notes -IIT JEE Main Maths – per latest Syllabus.
Key Concepts:
- Linear Differential Equations of Type \( \displaystyle \frac{dy}{dx} + P(x)y = Q(x) \)
- Differential Equations Reducible to Linear Form (Bernoulli’s Equation)
- Applications of Differential Equations — Growth and Decay, Newton’s Law of Cooling, and Motion Problems
Linear Differential Equations of Type \( \displaystyle \frac{dy}{dx} + P(x)y = Q(x) \)
A linear differential equation is an equation in which the dependent variable \( y \) and its derivative \( \dfrac{dy}{dx} \) appear only to the first power and are not multiplied together.
The standard form is: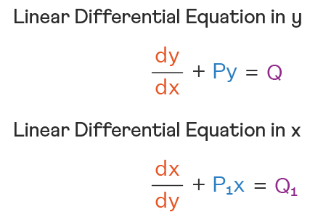
$ \dfrac{dy}{dx} + P(x)y = Q(x) $
Here,
- \( P(x) \) and \( Q(x) \) are known functions of \( x \).
- \( y \) is the dependent variable.
Standard Form and Integrating Factor (I.F.)
The equation is said to be in standard form if it can be written as:
$ \dfrac{dy}{dx} + P(x)y = Q(x) $
The Integrating Factor (I.F.)</strong) is defined as:
$ \text{I.F.} = e^{\int P(x)\,dx} $
General Solution
Multiplying both sides of the differential equation by the integrating factor:
$ e^{\int P(x)\,dx} \dfrac{dy}{dx} + e^{\int P(x)\,dx} P(x)y = Q(x)e^{\int P(x)\,dx} $
The left-hand side becomes the derivative of \( y \times \text{I.F.} \):
$ \dfrac{d}{dx}\left[y \cdot e^{\int P(x)\,dx}\right] = Q(x)e^{\int P(x)\,dx} $
Integrating both sides:
$ y \cdot e^{\int P(x)\,dx} = \int Q(x)e^{\int P(x)\,dx}\,dx + C $
Hence, the general solution is:
$ \boxed{y = e^{-\int P(x)\,dx}\left[\int Q(x)e^{\int P(x)\,dx}\,dx + C\right]} $
Steps to Solve
- Write the equation in standard form \( \dfrac{dy}{dx} + P(x)y = Q(x) \).
- Find the integrating factor \( \text{I.F.} = e^{\int P(x)\,dx} \).
- Multiply the entire equation by the I.F.
- Recognize that LHS = \( \dfrac{d}{dx}(y \cdot \text{I.F.}) \).
- Integrate both sides and solve for \( y \).
Special Case — When \( Q(x) = 0 \)
The equation reduces to:
$ \dfrac{dy}{dx} + P(x)y = 0 $
This is a homogeneous linear differential equation whose solution is:
$ y = Ce^{-\int P(x)\,dx} $
Example
Solve \( \dfrac{dy}{dx} + y = e^{-x} \).
▶️ Answer / Explanation
Step 1: Compare with standard form \( \dfrac{dy}{dx} + P(x)y = Q(x) \).
Here, \( P(x) = 1, \, Q(x) = e^{-x}. \)
Step 2: Find the integrating factor:
\( \text{I.F.} = e^{\int 1\,dx} = e^x. \)
Step 3: Multiply throughout by \( e^x \):
\( e^x\dfrac{dy}{dx} + e^x y = 1. \)
LHS = \( \dfrac{d}{dx}(y e^x) \). Hence,
\( \dfrac{d}{dx}(y e^x) = 1. \)
Step 4: Integrate both sides:
\( y e^x = x + C. \)
Step 5: Final Solution:
\( \boxed{y = e^{-x}(x + C).} \)
Example
Solve \( \dfrac{dy}{dx} + 2y = 4x \).
▶️ Answer / Explanation
Step 1: Standard form → \( P(x) = 2, \, Q(x) = 4x. \)
Step 2: Integrating Factor:
\( \text{I.F.} = e^{\int 2\,dx} = e^{2x}. \)
Step 3: Multiply the whole equation by \( e^{2x} \):
\( e^{2x}\dfrac{dy}{dx} + 2ye^{2x} = 4xe^{2x}. \)
LHS = \( \dfrac{d}{dx}(y e^{2x}) \). So,
\( \dfrac{d}{dx}(y e^{2x}) = 4xe^{2x}. \)
Step 4: Integrate both sides:
\( y e^{2x} = \int 4xe^{2x}\,dx. \)
Using integration by parts: \( \int xe^{2x}\,dx = \dfrac{xe^{2x}}{2} – \dfrac{e^{2x}}{4}. \)
\( \Rightarrow y e^{2x} = 4\left(\dfrac{xe^{2x}}{2} – \dfrac{e^{2x}}{4}\right) + C = 2xe^{2x} – e^{2x} + C. \)
Step 5: Divide by \( e^{2x} \):
\( \boxed{y = 2x – 1 + Ce^{-2x}.} \)
Example
Solve \( \dfrac{dy}{dx} + \dfrac{y}{x} = \sin x \), for \( x > 0 \).
▶️ Answer / Explanation
Step 1: Standard form: \( P(x) = \dfrac{1}{x}, \, Q(x) = \sin x. \)
Step 2: Integrating Factor:
\( \text{I.F.} = e^{\int 1/x\,dx} = e^{\ln x} = x. \)
Step 3: Multiply through by \( x \):
\( x\dfrac{dy}{dx} + y = x\sin x. \)
LHS = \( \dfrac{d}{dx}(xy). \)
\( \dfrac{d}{dx}(xy) = x\sin x. \)
Step 4: Integrate both sides:
\( xy = \int x\sin x\,dx. \)
Integration by parts: \( \int x\sin x\,dx = -x\cos x + \sin x. \)
\( \Rightarrow xy = -x\cos x + \sin x + C. \)
Step 5: Final Solution:
\( \boxed{y = -\cos x + \dfrac{\sin x}{x} + \dfrac{C}{x}.} \)
Differential Equations Reducible to Linear Form (Bernoulli’s Equation)
Some first-order differential equations are not linear in \( y \) but can be converted to a linear form by a suitable substitution. A very important class of such equations is known as Bernoulli’s Equations.
Bernoulli’s Differential Equation — Standard Form
The standard form of Bernoulli’s equation is:
$ \dfrac{dy}{dx} + P(x)y = Q(x)y^n $
where \( n \neq 0, 1 \).
- If \( n = 0 \), it becomes a linear differential equation \( \dfrac{dy}{dx} + P(x)y = Q(x) \).
- If \( n = 1 \), it becomes a separable equation \( \dfrac{dy}{dx} = Q(x) – P(x)y \).
Method of Solving Bernoulli’s Equation
- Divide both sides by \( y^n \) (to make the right side contain only \( Q(x) \)).
- Make the substitution \( y^{1-n} = z \).
- Differentiate: \( \dfrac{dz}{dx} = (1 – n)y^{-n}\dfrac{dy}{dx} \).
- Substitute this in the given equation to obtain a linear equation in \( z \).
- Solve the resulting linear differential equation using the Integrating Factor (I.F.) method.
Derivation Outline
Starting with \( \dfrac{dy}{dx} + P(x)y = Q(x)y^n \):
Divide by \( y^n \): $ y^{-n}\dfrac{dy}{dx} + P(x)y^{1-n} = Q(x) $
Now put \( y^{1-n} = z \Rightarrow \dfrac{dz}{dx} = (1-n)y^{-n}\dfrac{dy}{dx}. \)
Substitute into the equation:
$ \dfrac{1}{1-n}\dfrac{dz}{dx} + P(x)z = Q(x) $
Multiply both sides by \( 1-n \):
$ \dfrac{dz}{dx} + (1-n)P(x)z = (1-n)Q(x) $
This is a linear equation in \( z \).
Example
Solve \( \dfrac{dy}{dx} + y = y^2 \).
▶️ Answer / Explanation
Step 1: Here, \( P(x) = 1, Q(x) = 1, n = 2. \)
Equation: \( \dfrac{dy}{dx} + y = y^2. \)
Step 2: Divide by \( y^2 \): \( y^{-2}\dfrac{dy}{dx} + \dfrac{1}{y} = 1. \)
Step 3: Substitution \( y^{1-n} = y^{-1} = z. \)
\( \dfrac{dz}{dx} = -y^{-2}\dfrac{dy}{dx}. \)
So, \( -\dfrac{dz}{dx} + \dfrac{1}{y} = 1. \)
But \( \dfrac{1}{y} = z. \Rightarrow -\dfrac{dz}{dx} + z = 1. \)
Step 4: Simplify: \( \dfrac{dz}{dx} – z = -1. \)
Step 5: Integrating factor: \( e^{\int -1\,dx} = e^{-x}. \)
Multiply throughout by \( e^{-x} \): \( e^{-x}\dfrac{dz}{dx} – ze^{-x} = -e^{-x}. \)
LHS = \( \dfrac{d}{dx}(ze^{-x}) \). So, \( \dfrac{d}{dx}(ze^{-x}) = -e^{-x}. \)
\( ze^{-x} = \int -e^{-x}dx = e^{-x} + C. \)
\( z = 1 + Ce^{x}. \)
Step 6: Substitute back \( z = 1/y \): \( \dfrac{1}{y} = 1 + Ce^{x}. \)
Final Answer: \( \boxed{y = \dfrac{1}{1 + Ce^{x}}.} \)
Example
Solve \( \dfrac{dy}{dx} + \dfrac{2y}{x} = 3xy^2 \), where \( x > 0 \).
▶️ Answer / Explanation
Step 1: Compare with \( \dfrac{dy}{dx} + P(x)y = Q(x)y^n \): \( P(x) = \dfrac{2}{x}, Q(x) = 3x, n = 2. \)
Step 2: Divide by \( y^2 \): \( y^{-2}\dfrac{dy}{dx} + \dfrac{2y^{-1}}{x} = 3x. \)
Step 3: Put \( y^{-1} = z \Rightarrow \dfrac{dz}{dx} = -y^{-2}\dfrac{dy}{dx}. \)
Substitute: \( -\dfrac{dz}{dx} + \dfrac{2z}{x} = 3x. \)
\( \Rightarrow \dfrac{dz}{dx} – \dfrac{2z}{x} = -3x. \)
Step 4: Integrating Factor: \( \text{I.F.} = e^{\int -\frac{2}{x}dx} = e^{-2\ln x} = x^{-2}. \)
Step 5: Multiply through by \( x^{-2} \): \( x^{-2}\dfrac{dz}{dx} – \dfrac{2z}{x^3} = -3. \)
LHS = \( \dfrac{d}{dx}(z x^{-2}) \). Hence, \( \dfrac{d}{dx}(z x^{-2}) = -3. \)
Integrate both sides: \( z x^{-2} = -3x + C. \)
\( z = -3x^3 + Cx^2. \)
Step 6: Substitute \( z = \dfrac{1}{y} \): \( \boxed{\dfrac{1}{y} = -3x^3 + Cx^2.} \)
Example
Solve \( \dfrac{dy}{dx} – \dfrac{y}{x} = x^2y^3 \).
▶️ Answer / Explanation
Step 1: \( P(x) = -\dfrac{1}{x}, \, Q(x) = x^2, \, n = 3. \)
Step 2: Divide both sides by \( y^3 \): \( y^{-3}\dfrac{dy}{dx} – \dfrac{y^{-2}}{x} = x^2. \)
Step 3: Let \( y^{1-n} = y^{-2} = z \Rightarrow \dfrac{dz}{dx} = -2y^{-3}\dfrac{dy}{dx}. \)
Substitute into equation:
\( -\dfrac{1}{2}\dfrac{dz}{dx} – \dfrac{z}{x} = x^2. \)
Multiply both sides by \( -2 \): \( \dfrac{dz}{dx} + \dfrac{2z}{x} = -2x^2. \)
Step 4: I.F. \( = e^{\int \frac{2}{x}dx} = e^{2\ln x} = x^2. \)
Step 5: Multiply through by \( x^2 \): \( x^2\dfrac{dz}{dx} + 2xz = -2x^4. \)
LHS = \( \dfrac{d}{dx}(x^2z) = -2x^4. \)
Integrate both sides: \( x^2z = -\dfrac{2x^5}{5} + C. \)
\( z = -\dfrac{2x^3}{5} + \dfrac{C}{x^2}. \)
Step 6: Substitute \( z = y^{-2} \): \( \boxed{y^{-2} = -\dfrac{2x^3}{5} + \dfrac{C}{x^2}.} \)
Applications of Differential Equations — Growth and Decay, Newton’s Law of Cooling, and Motion Problems
Differential equations are used to model many real-life physical and natural processes, such as population growth, radioactive decay, cooling of objects, and motion under gravity. Each of these processes is governed by the rate of change of a quantity with respect to time or another variable.
Exponential Growth and Decay
When the rate of change of a quantity is proportional to the quantity itself, the process follows exponential growth or decay.
$ \dfrac{dy}{dt} = ky $
where:
- \( y \): the quantity at time \( t \)
- \( k \): proportionality constant
Solution:
$ \int \dfrac{dy}{y} = \int k\,dt \Rightarrow \ln y = kt + C \Rightarrow y = Ae^{kt} $
- If \( k > 0 \), exponential growth.
- If \( k < 0 \), exponential decay.
Example
A bacteria population doubles in 3 hours. If the initial population is 500, find the population after 9 hours.
▶️ Answer / Explanation
Let \( y \) be the population at time \( t \).
\( \dfrac{dy}{dt} = ky \Rightarrow y = Ae^{kt}. \)
At \( t = 0, y = 500 \Rightarrow A = 500. \)
At \( t = 3, y = 1000 \Rightarrow 1000 = 500e^{3k} \Rightarrow e^{3k} = 2 \Rightarrow k = \dfrac{\ln 2}{3}. \)
At \( t = 9 \): \( y = 500e^{9k} = 500e^{3(\ln 2)} = 500(2^3) = 4000. \)
Answer: Population after 9 hours = 4000.
Radioactive Decay
In radioactive decay, the rate of disintegration of nuclei is proportional to the amount of undecayed material present at that moment.
$ \dfrac{dN}{dt} = -\lambda N $
where \( \lambda \) is the decay constant.
Solution:
$ N = N_0 e^{-\lambda t} $
- \( N_0 \): initial amount of substance
- \( N \): remaining amount after time \( t \)
Example
A radioactive substance loses 20% of its mass in 5 years. Find its half-life.
▶️ Answer / Explanation
Given: \( N = 0.8N_0 \) when \( t = 5. \)
\( N = N_0 e^{-\lambda t} \Rightarrow 0.8 = e^{-5\lambda}. \)
Taking logs: \( \lambda = -\dfrac{1}{5}\ln(0.8) = 0.0446. \)
For half-life \( T \), \( N = \dfrac{N_0}{2} \): \( \dfrac{1}{2} = e^{-\lambda T} \Rightarrow T = \dfrac{\ln 2}{\lambda} = \dfrac{0.693}{0.0446} \approx 15.54 \text{ years.} \)
Answer: Half-life ≈ 15.5 years.
Newton’s Law of Cooling
The rate of change of temperature of a body is proportional to the difference between its temperature and the surrounding temperature.
$ \dfrac{dT}{dt} = -k(T – T_s) $
where:
- \( T \): temperature of the body at time \( t \)
- \( T_s \): surrounding temperature (constant)
- \( k \): positive constant
Solution:
$ T – T_s = (T_0 – T_s)e^{-kt} $
where \( T_0 \) is the initial temperature of the body.
Example
The temperature of a body cools from \( 80^\circ C \) to \( 60^\circ C \) in 10 minutes, when the surrounding temperature is \( 20^\circ C \). Find the temperature after 20 minutes.
▶️ Answer / Explanation
Using \( T – 20 = (80 – 20)e^{-kt} \Rightarrow T – 20 = 60e^{-kt}. \)
At \( t = 10, T = 60 \): \( 60 – 20 = 60e^{-10k} \Rightarrow 40 = 60e^{-10k} \Rightarrow e^{-10k} = \dfrac{2}{3}. \)
\( k = \dfrac{1}{10}\ln\dfrac{3}{2} = 0.04055. \)
At \( t = 20 \): \( T – 20 = 60e^{-20k} = 60e^{-0.811} = 60(0.445) = 26.7. \)
Temperature after 20 min: \( T = 46.7^\circ C. \)
Motion Problems — Velocity and Acceleration
If the rate of change of velocity (acceleration) depends on velocity or position, it can often be modeled as a differential equation.
Example forms:
- \( \dfrac{dv}{dt} = k(v_t – v) \) — approach to terminal velocity
- \( \dfrac{dv}{dt} = -kv \) — resistive medium (exponential decay in velocity)
Example
A particle falling under gravity experiences air resistance proportional to its velocity. If its terminal velocity is \( 50 \, \text{m/s} \), find its velocity after 5 s. Assume \( g = 10 \, \text{m/s}^2. \)
▶️ Answer / Explanation
Equation of motion: \( \dfrac{dv}{dt} = g – kv. \)
At terminal velocity, \( \dfrac{dv}{dt} = 0 \Rightarrow g = kv_t \Rightarrow k = \dfrac{g}{v_t} = \dfrac{10}{50} = 0.2. \)
\( \Rightarrow \dfrac{dv}{dt} = 10 – 0.2v. \)
Integrate using separable variables:
\( \int \dfrac{dv}{10 – 0.2v} = \int dt. \)
\( -5\ln|10 – 0.2v| = t + C. \)
At \( t = 0, v = 0 \): \( -5\ln 10 = C. \)
At \( t = 5 \): \( -5\ln|10 – 0.2v| = 5 – 5\ln 10 \Rightarrow \ln|10 – 0.2v| = -1 + \ln 10. \)
\( 10 – 0.2v = 10e^{-1} \Rightarrow v = 50(1 – e^{-1}) \approx 31.6 \, \text{m/s}. \)
Answer: Velocity after 5 s = 31.6 m/s.
